本文主要是介绍狂神说的全部笔记_数学有必要记笔记吗?好的数学笔记怎么做?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

很多同学都没有记数学笔记的习惯,尤其在上高中之前,觉得只要会做题就可以了,没必要记笔记。但是上了高中后知识点增多,就会出现复习时突然想到某个知识点老师讲过,回去翻书却耗费了大量时间的情况。
还有一些同学很喜欢记笔记,但是对笔记的认知却总是不得其法,停留在这种情况:上课听讲的时候奋笔疾书拼命记笔记,课后却很少看自己的笔记;看别人记笔记既好看又高效,你一记却变成了抄书......
如果你到现在都仍然觉得判断笔记好坏的标准就是字迹是否工整,或者觉得笔记是个可有可无的存在,建议你认真阅读本文,相信你的学习状态很快会得到改善。

好笔记的作用究竟是什么?
从结果来看,好的笔记是信息记录的呈现。

图片来自网络
这样的笔记有助于帮助你在考前找到复习重点,快速了解基础知识,避免基础知识不牢固回去翻书的恶习,提升学习效率。
从过程看,好的笔记可以锻炼大脑、深化思考。
专攻神经内科的日本医学博士、《笔记成功术》作者米山公启指出,书写的过程本身,就是一连串的数据辨识与思考延伸,不但可以刺激人触类旁通,提升个人的信息敏感程度,更是最便利的思维活动锻炼。
笔记的书写是一套信息判断与分析的流程。一个人只有在听课时完整接收所有信息,然后用大脑对信息进行处理,才能将重点内容最终呈现在笔记本上。
尤其在你课后整理笔记的过程中,再度审视你的笔记内容,去芜存菁,重点标记,分类索引,都能让你对所学到的知识进行深刻记忆。
但即便如此,仍有很多人不习惯记笔记,甚至认为这是在浪费时间。

为什么很多人觉得记笔记在浪费时间呢?
18年冬天,我在山东讲课时遇到一名高三同学,她特别有礼貌的向我请教:
“老师,我现在数学成绩在100分左右上不去,要怎么做才能得到提升呢?学校老师和我说要有错题本,可是错题本对我根本没有用啊。”
我听完什么都没有说,只是反问她:那你记完错题后有反复重做吗?
没有。
很多同学都像她一样,一开始就被老师要求,你要准备一个笔记本一个错题本,每天坚持记。然后大家像完任务一样,中规中矩的上课记笔记下课抄错题,有时候老师不检查就偷偷犯懒不去做。
绝大多数人都把记笔记当成了一项抄写任务,而忽略了笔记的本质。
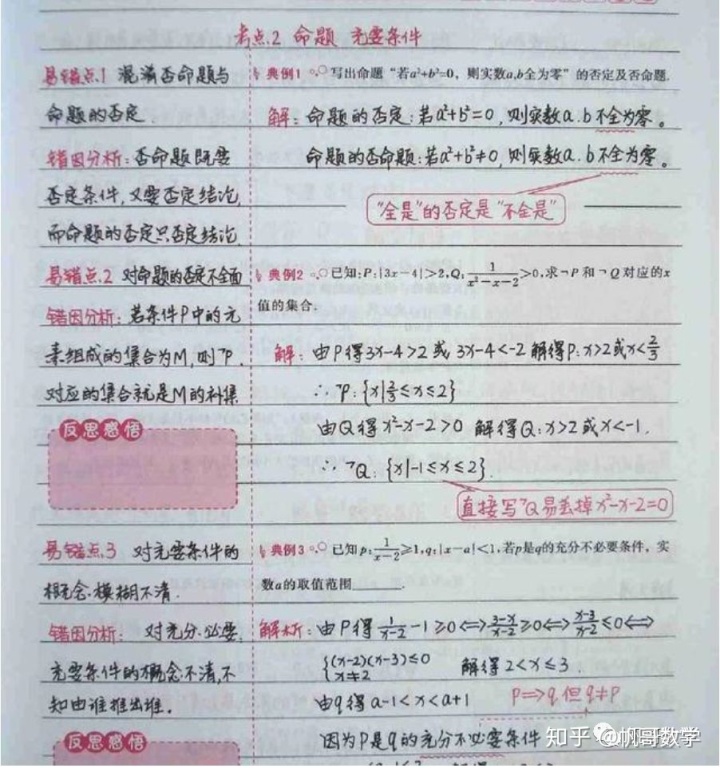
图片来自网络
正如我们之前所说,好的笔记可以锻炼大脑深化思考,但是如果你把笔记变成了单纯的抄写活动,没有经过思考,没有理解笔下的内容。那么这本笔记永远都还是别人的笔记。
错题本也是一样。
数学学不好的很大原因在错题集上,因为这里集合了你所有没有掌握的数学精华。这应该成为你考前复习的重点才对。
但如果,你的错题集只是照搬,没有融合自己的思想,这本错题集还是别人的,与自己无关。

好的笔记应该怎么做?
很多同学平时其实是不爱记数学笔记的,在这里我以数学笔记为例来讲,但也同时适用于其他学科。
1. 梳理基础知识点
在你刚刚接触数学的时候,你的脑中并没有整个知识体系,可以按照老师讲课和课本的顺序逐节记录。
内容包括:不太懂的概念、定理和公式,推理思路。切忌不要把老师讲的内容全部记下来,你要记的是有助于你理解和加深记忆的内容。
为什么这样做:
记录全部内容太耗时间,不利于你充分调动大脑去思考;
记录全部内容会让你停留在你已经拥有了这段知识的错觉中,后期忽视复习。
课后复习时,将重难点用不同颜色的笔进行标记,重点需要加强记忆,难点需要加强理解。
下一章节另起一页开始记,不要混在一起。
2. 记录典型错题
无论是高中还是考研,数学的学习一定有一个刷题的过程,对于错题的整理记录是必不可少的。
切记,不是每一道错题都要整理进错题本中。要先分析做错的原因,如果是因为粗心做错则不需要整理到错题本中。
定期复习重做错题,确定掌握的题可以剔除出去。
个人建议记笔记用活页笔记本。每个学期期中期末复习的时候重新进行整理,把同一知识点的题型和基础知识归类到一起,活页笔记本整理起来会非常方便。
后期如果知识点变多可以利用彩色标签建立分类索引,方便迅速查找。

关于记笔记,想说的很多,小到平时上课听讲,大到以后生活的方方面面,听课、读书、工作、开会,都会记笔记。记笔记的重要性可见一斑。
记笔记的方法也有千千万,但是任何一种方法,如果你不去执行,它都不可能会产生作用。
时间长了,每个人都会形成自己的笔记风格,但是它的本质是不变的。笔记是一个由薄变厚,再由厚变薄的过程,不断整理和复习时学好知识记好笔记的关键所在。
希望你能通过本文获得启发,找到适合自己的办法,坚持并养成记笔记的习惯,必将帮你提高学习效率,事半功倍。
这篇关于狂神说的全部笔记_数学有必要记笔记吗?好的数学笔记怎么做?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









