链表面试题(动图详解)-明明做出来了却为什么没有Offer?

相关推荐（面试专栏查看更多）

• 链表面试题(动图详解)-明明做出来了却为什么没有Offer?
• 二叉树面试题-你已经是棵成熟的二叉树了，要学会自己解题
• 数组面试题-大力出奇迹？

面试题明明做出来了，为什么最后没有Offer？
虽然实现了功能，但是可能忽略了性能和细节，比如说复杂度、边界条件、空指针等。就是所谓的鲁棒性(Robus)问题，本文将介绍几个经典链表面试题。

从尾到头打印链表

题目：输入一个链表的头节点，从尾到头反过来打印每个节点的值。

第一反应可能是把链表指针反转过来，然后从头到尾的输出。但是通常打印是一个只读操作并不希望修改内容，最好问清楚面试官。

从尾到头打印链表，$O(n)$复杂度是肯定的，但是我们遍历链表的顺序只能从头到尾，而打印要求是从尾到头。这不就是典型的“先进后出”吗？那么我们就可以使用栈来解决，而想到栈，我们还可以想到系统栈，即递归来解决。至于选择哪种，可以看链表长度决定，若长度不长则递归实现，反之栈实现。

实现代码：

#include<bits/stdc++.h>
using namespace std;
//只会C的小白强烈建议学一下C++
//特别是STL，算法比赛帮助很大
struct node{int val;node* next;//构造器（后继节点默认空指针） node(int v,node* n=nullptr){val=v;next=n;} 
};
void method1(node* head){  //栈方法 stack<node*>st;node* p =head;while(p!=nullptr){  //从头到尾入栈 st.push(p);p=p->next;}while(!st.empty()){  //出栈并打印 p=st.top();  //栈顶 st.pop();  //出栈 printf("%d ",p->val); } 
}
void method2(node* head){  //递归方法 if(head!=nullptr){method2(head->next);printf("%d ",head->val);}
}
int main(){node* head=new node(1);node* tail=head;for(int i=2;i<=5;i++){//创建长度为5的链表 node* p=new node(i);tail->next=p;tail=p; }method1(head);method2(head);return 0;
}
//运行结果：5 4 3 2 1 5 4 3 2 1

反转链表

题目：反转链表并输出反转后链表的头节点

其实这题不难，就像交换两杯水一样，需要第三个空杯子来做周转。那么反转链表时，需要三个指针分别指向当前遍历节点、前驱节点、后继节点即可完成指针顺序的交换。
示意图：

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node(int v,node* n=nullptr){val=v;next=n;} 
};
node* reverse(node* head){node* reHead=nullptr;//反转后头指针node* cur=head;//记录当前遍历节点 node* pre=nullptr;//记录前驱节点while(cur!=nullptr){node* nex=cur->next;//记录后继结点 if(nex==nullptr) reHead=cur;//反转结束cur->next=pre;pre=cur;cur=nex; }return reHead;
}
int main(){node* head=new node(1);node* tail=head;for(int i=2;i<=5;i++){node *p=new node(i);tail->next=p;tail=p;}node* reHead=reverse(head);while(reHead!=nullptr){printf("%d ",reHead->val);reHead=reHead->next;}return 0;
}
//运行结果：5 4 3 2 1

O(1)删除链表节点

题目：在$O(1)$时间内删除链表节点。
给定单向链表的头指针和一个节点指针，定义一个函数在$O(1)$内删除该节点。

第一反应无疑是从头节点开始顺序遍历查找要删除的节点（并记录前一个节点），然后将它前一个节点的next指向被删节点的下一个节点，最后删除被删节点。如下图：

可是这种思路需要顺序查找，复杂度是$O(n)$肯定不行，哪有这么容易。

之所以要从头开始顺序查找，是因为要找到它的前一个节点，不然链表会断开。再思考一下，我们其实可以很方便的得到被删节点的下一个节点，考虑如何转换？

答案是把下一个节点内容覆盖到被删节点，然后把下一个节点删除，这不就相对于删除了被删节点吗？！而且复杂度是$O(1)$，如下图：

但是还存在BUG（你以为这就有Offer了？），如果被删节点是尾节点，那么它就不存在下一个节点，如果直接删除，那它的前一个节点的next指针就是野指针，存在漏洞，此时该方法就不适用了，只能笨方法乖乖顺序查找它的前一个节点。平均复杂度是$[(n-1)\ast O(1)+O(n)]/n=O(1)$。

你以为这就完了？（天真），如果链表中只有一个节点，即被删节点是头节点也是尾节点，那么我们在删除被删节点后，还要把头节点置为nullptr，小心野指针。最后注意判断下空指针。

其实还有一种可能，被删节点不在链表中。但又受到$O(1)$复杂度的限制，这样只能把检查责任推给调用者了（又要马儿跑又要马儿不吃草），可以与面试官探讨，体现考虑问题周全。

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node(int v,node* n=nullptr){val=v;next=n;} 
};
void solve(node* head,node* del){if(head==nullptr||del==nullptr)return;//判断空指针if(del->next==nullptr){//删尾节点情况 node* pre = head; //顺序查找前驱节点 while(pre->next!=del)pre=pre->next;pre->next=nullptr;delete del;del=nullptr; }else if(head==del){ //只有一个节点 delete del;del=nullptr;head=nullptr;}else{ //覆盖并删后继节点 node* nex=del->next;del->val=nex->val;del->next=nex->next;delete nex;nex=nullptr; }
}
int main(){node* head=new node(1);node* tail=head;node* del = nullptr;//被删节点 for(int i=2;i<=5;i++){node* p=new node(i);tail->next=p;tail=p;if(i==3)del=p;//设删3号节点 }solve(head,del);while(head != nullptr){ //可以打印康康 printf("%d ",head->val);head=head->next;}return 0;
}
//运行结果：1 2 4 5

链表中倒数第k个节点

题目：输出单向链表中的倒数第k个节点

很自然的想到先走到链表尾端，再从尾端回溯k步，但单向链表明显是行不通的。或者遍历两次，第一次统计链表长度，第二次遍历n-k次。这种思路固然能实现，但是其实还有更优的解法，只需遍历一次。

答案是利用双指针。第一个指针从头指针开始遍历向前走k-1步，此时第二个指针不动；从第k步开始，第二个指针也开始从头指针遍历向前走。这样两个指针的距离就保持在了k-1，当地一个指针走到尾部时，第二个指针则正好是倒数第k个。
上动图：

但是还是要注意防坑，需要处理空指针、链表长度小于k、k<1等情况。

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node(int v,node* n=nullptr){val=v;next=n;} 
};
node* findK(node *head,int k){if(head==nullptr||k<1)return nullptr;node* p1=head;node* p2=head;for(int i=0;i<k-1;i++){  //p1先走k-1步 if(p1->next!=nullptr)p1=p1->next; else return nullptr;}while(p1->next!=nullptr){  //然后同时走 p1=p1->next;p2=p2->next;}return p2;
}
int main(){node* head=new node(1);node* tail=head;for(int i=2;i<=5;i++){node* p=new node(i);tail->next=p;tail=p;}node* k=findK(head,3);//设找倒数第三个printf("%d",k==nullptr?-1:k->val);return 0;
}
//运行结果：3

（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

链表中环的入口节点

题目：如果一个链表包含环，如何找出环的入口节点？

第一反应不会？
解决问题第一步是如何确定链表中包含环？受上一题启发，尝试用双指针解决问题。让一个指针一次走一步，另一个指针一次走两步，当走得快得指针追上了走得慢得指针时，那么就说明链表有环。反之如果走得快的指针走到了链表末尾都没有追上，则链表无环。

确定有环后，又该如何找到环的入口呢？还是使用双指针来解决，设链表中的环有n个节点，则第一个指针先走n步，然后两个指针以相同的速度前进，当第二个指针指向环的入口时，第一个指针已经绕着环走了一圈也到了入口处，两指针相遇。

那现在的问题是如何求得环中节点数目n？我们刚刚在判断有无环时用了一快一慢两指针，若两指针相遇则说明有环。我们可以从这个节点出发，一边向前移动一边计数，当再次回到这个节点时，就可以得到环的数目了（妙啊）。

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node(int v,node* n=nullptr){val=v;next=n;} 
};
node* isLoop(node* head){//判断环并返回相遇点 if(head==nullptr||head->next==nullptr)return nullptr;//千年老坑空指针 node* pSlow=head;node* pFast=head;while(pSlow!=nullptr&&pFast!=nullptr){pSlow=pSlow->next;//慢的走一步 pFast=pFast->next;//快的走两步 if(pFast!=nullptr)pFast=pFast->next;if(pSlow==pFast)return pSlow;}return nullptr; 
}
node* enter(node* head){node* met=isLoop(head);if(met==nullptr)return nullptr;int cnt=1;//记录环中节点数node* p1=met;while(p1->next!=met){p1=p1->next;cnt++;} p1=head;//p1先走cnt步 for(int i=0;i<cnt;i++)p1=p1->next;node* p2=head;while(p1!=p2){  //然后同时走 p1=p1->next;p2=p2->next;}return p1; 
}
int main(){node* head=new node(1);node* tail=head;node* loop=nullptr; for(int i=2;i<=5;i++){node *p=new node(i);tail->next=p;tail=p;if(i==3)loop=p;}tail->next=loop;//设置环5->3node* ans=enter(head);printf("%d",ans==nullptr?-1:ans->val);return 0;
}
//运行结果：3

合并两个排序的链表

题目：输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

分析从合并两个链表的头节点开始，若链表1的头节点值小于链表2的头节点值，就把链表1的头节点作为合并后链表的头节点，然后继续比较剩余节点，仍是有序的，因此合并步骤和之前一样，我们就可以定义递归来完成。

下面解决鲁棒性问题，首先千年老坑空指针，若不加以判断直接访问空指针报错无疑，若一个链表是空指针，则直接返回另一个链表即可。另外面试官不给你Offer，可能是因为你开辟了另外的内存空间存储合并后的链表，而合并前的链表空间未释放等。直接使用递归修改指针方向即可。

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node(int v,node* n=nullptr){val=v;next=n;} 
};
node* merge(node* head1,node* head2){if(head1==nullptr)return head2;if(head2==nullptr)return head1;node* merHead=nullptr;if(head1->val<head2->val){merHead=head1;merHead->next=merge(head1->next,head2);}else{merHead=head2;merHead->next=merge(head1,head2->next);}return merHead;
}
int main(){node* head1=new node(1);node* tail1=head1;for(int i=3;i<=9;i+=2){node *p=new node(i);tail1->next=p;tail1=p;}node* head2=new node(2);node* tail2=head2;for(int i=4;i<=8;i+=2){node *p=new node(i);tail2->next=p;tail2=p;}node* merHead=merge(head1,head2);while(merHead!=nullptr){printf("%d ",merHead->val);merHead=merHead->next;}return 0;
}
//运行结果：1 2 3 4 5 6 7 8 9

复杂链表的复制

题目：实现函数赋值一个复杂链表。
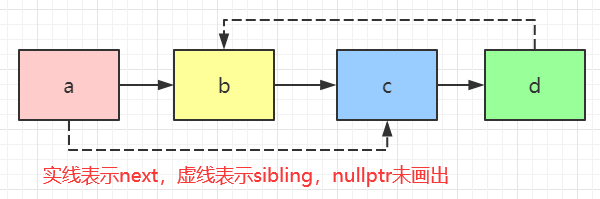
在复杂链表中，每个节点除了有一个next指针指向下一个节点外，还有一个sibling指针指向链表中任意节点或者nullptr。

第一反应可能是先复制链表上每个节点，并用next链接起来，然后设置每个节点的sibling指针。但是复制后节点N’的sibling指针所指节点S’可能在N’的前面也可能在N’的后面，所以定位S’需要从头节点开始找，因此这种方法的复杂度是$O(n^2)$，不然只能以空间换时间，用哈希表记录以便在$O(1)$内找到S’。

其实还有更好的解决方法：

1. 先根据原始链表的每个节点N创建对应的N’，再把N’链接到N的后面；
2. 设置复制出来的N’sibling指针指向原S的next（即S’）；
3. 拆分链表，奇数位置用next链接起来就是原链表，偶数位置用next链接起来就是复制所得链表。

核心是理解第2步，巧妙的用S->next=S'当作哈希表，而又通过N->sibling=S可以在$O(1)$内找到N’所指的S’，即没有额外申请空间，又在$O(n)$复杂度内完成，真是妙啊。

示意图：

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node* sibling;node(){}node(int v,node* n=nullptr,node* s=nullptr){val=v;next=n;sibling=s;} 
};
void clone(node* head){ //复制链表 node* p=head;while(p!=nullptr){node*  pclone=new node(p->val);pclone->next=p->next;p->next=pclone;p=pclone->next;}
}
void connectSib(node* head){  //链接sibLing指针 node* p=head;while(p!=nullptr){node* pclone=p->next; //指向它的下一个复制节点 if(p->sibling!=nullptr)pclone->sibling=p->sibling->next;p=pclone->next;//下一组 } 
}
node* split(node* head){  //拆分链表 node* pNode=head;node* pCloneHead=nullptr;node* pCloneNode=nullptr;if(pNode!=nullptr){ //处理头指针 pCloneHead=pCloneNode=pNode->next;//指向复制第一个 pNode->next=pCloneNode->next;pNode=pNode->next;//下一组 }while(pNode!=nullptr){pCloneNode->next=pNode->next;pCloneNode=pCloneNode->next;pNode->next=pCloneNode->next;pNode=pNode->next; }return pCloneHead;
} 
int main(){//构建复杂链表 node* head=new node(1);node* tail=head;node* t1=nullptr;node* t2=nullptr;for(int i=2;i<5;i++){node *p=new node(i);tail->next=p;tail=p;if(i==2)t1=p;else if(i==3)t2=p;}head->sibling=t2;tail->sibling=t1;//复制、链接、拆分 clone(head);connectSib(head);node* copyHead=split(head);printf("原链表：\n"); node* p=head;while(p!=nullptr){printf("val:%d，sib:%d\n",p->val,p->sibling==nullptr?-1:p->sibling->val);p=p->next;}printf("复制后链表：\n"); p=copyHead;while(p!=nullptr){printf("val:%d，sib:%d\n",p->val,p->sibling==nullptr?-1:p->sibling->val);p=p->next;}return 0;
}
/*运行结果：
原链表：
val:1，sib:3
val:2，sib:-1
val:3，sib:-1
val:4，sib:2
复制后链表：
val:1，sib:3
val:2，sib:-1
val:3，sib:-1
val:4，sib:2
*/

两个链表的第一个公共节点

题目：输入两个链表，找到他们的第一个公共节点

第一反应可能是直接暴力，在第一个链表上遍历每个节点，每遍历一个节点又在第二个链表上遍历查找，时间复杂度是$O(nm)$。想都不用想，事情不会这么简单。

首先分析有公共节点的两链表特点，由于是单向链表，因此从第一个公共节点以后的部分都是重合的，形状类似一个Y。

那如果我们从两个链表的尾部开始往前比较，那么最后一个相同的节点就是我们要找的节点。可问题是单向链表只能从头指针开始向后顺序遍历，怎样从尾到头遍历，这就是文章第一题先进后出用到的栈了（首尾呼应，不愧是我）。把两个链表分别放到两个栈里，出栈并判断是否相同即可，复杂度是$O(m+n)$。

其实我们也可以不借助栈来实现。可以先遍历两个栈分别获取两链表的长度，知道长链表比短链表多几个节点，然后多的这几个节点肯定不是第一个公共节点，可以让长链表先走这几步，然后两个链表再一起向后走，遇到的第一个相同节点就是答案了。这种方法时间复杂度也是$O(m+n)$，但是提高了空间效率。

实现代码：

#include<bits/stdc++.h>
using namespace std;
struct node{int val;node* next;node(int v,node* n=nullptr){val=v;next=n;} 
};
int getLength(node* head){int length=0;node* p=head;while(p!=nullptr){length++;p=p->next;}return length;
}
node* common(node* head1,node* head2){int l1=getLength(head1);int l2=getLength(head2);int def=abs(l1-l2);node* pLong=head1;//长链表 node* pShort=head2; //短链表 if(l1<l2)swap(pLong,pShort);for(int i=0;i<def;i++)//长链表先走def步 pLong=pLong->next;while(pLong!=nullptr&&pShort!=nullptr){ //一起走 if(pLong==pShort)break;//找到答案 pLong=pLong->next;pShort=pShort->next; } return pLong;
} 
int main(){//创建两个含公共节点的链表 node* head1=new node(1);node* tail1=head1;node* same=nullptr;for(int i=2;i<=5;i+=2){node *p=new node(i);tail1->next=p;tail1=p;if(i==4)same=p;//设公共节点为4 }node* head2=new node(11);node* tail2=head2;node *p=new node(22);tail2->next=p;tail2=p;tail2->next=same;node* con=common(head1,head2);printf("公共节点:%d",con==nullptr?-1:con->val);return 0;
}
//运行结果：
//公共节点:4

原创不易，请勿转载（本不富裕的访问量雪上加霜 ）
博主首页：https://wzlodq.blog.csdn.net/
微信公众号：吾仄lo咚锵
如果文章对你有帮助，记得一键三连❤