本文主要是介绍数据库应用-Datalog,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Relational Algebra
数据库系统中引入的relational algebra并不多,大部分可由多个基本的operation结合而来
minimal Relational algebra: Ω=π,σ,⋈,β,∪,−
安全访问(sichere Anfragen)
所谓安全访问,就是指无论在何种数据库状态(Datenbankzustand)下,都能得到有限个结果的访问//什么叫数据库状态,还没搞清楚????
举个反例:{ x,y|¬R(x,y) } ; x,y∈N
为什么要用Logik作为访问语言
1.认识一种新的关系数据模型的访问语言,并且他们在表达能力上存在差别
2.Datalog做为一种基于Logik的访问语言,他与Relational Algebra等存在显著的区别。他有更加严谨的语言格式,这在带来一些有点的同时,也限制了他的可扩展性。学习Datalog可以开阔我们的视野
//这都是什么Motivation啊
3.Datalog可以表达一些Relational Algebra无法表达的问题,比如递归问题(z.B Transitive Huelle)
Logik的三个基本概念
Belegung:(翻译成分配不知道对不对)给一个变量分配一个值
Interpretation:(解释)就是signatur到konstant的映射 I:∑→ {T,F}
Modell:表达为真得Belegung
//详细的就看形式系统吧(Formal System)
例子: val(A1)=1,val(A2)=0 是Belegung,但不是Modell
//表达逻辑 和谓词逻辑有什么区别呢????
下面是谓词逻辑:
besuchtVorlesung(x) ⇒bestehtPruefung(x)
从一个确定的值域里面取值给一个变量赋值
Datalog//我还是Google一下datalog再说吧
Datalog是Prolog的子集(Teilmenge von Prolog)
基本例子:
关系:Person(Name,Age,Sex) Parent(Father,Mother)
father(X,Y):-Person(X,_,m),Parent(X,Y)
其中Person和Parent属于basis DB(Extensional Datenbank:EDB),father属于intentional Datenbank(IDB,即推到出来的 view)
基本例子2:
访问:
?-Mutter(X,Annie)
Mather(X,Y):-Person(X,_w),Parent(X,Y)
根据IDB规则查表找出Annie的母亲
问题:一个表达逻辑的可实现性是很难判断的,因此设置范围是很必要的
基本概念:
Atom://这就不说了
Literal: ¬ Atom或Atom
Klausel:Literal的析取
Horn-Klausel:·最多含有一个正的Atom的Klausel
Datalog-Programm: 有限个Horn-Klausel的集合
Horn-Klausel的例子:
Ancestor(X,Y):-Parent(X,Y)
Ancestor(X,Y):-Parent(X,Z),Ancestor(Z,Y)
//倒数第三个有点不懂??
Recursion
Datalog可以实现Recursion,比如
Ancestor(X,Y):-Parent(X,Y)
Ancestor(X,Y):-Parent(X,Z),Ancestor(Z,Y)
IDB pradicate(如Ancestor)即可以在头部,也可以在躯干部分
用relational algebra则无解
**问题:**Recursion in Datalog和前面的transitiver Hülle有什么区别呢??//不知啊 好像前面transitiver Hülle 也木写的样子???一样??
Fixpunkt:即f(x)=x
运行算法:
IDB 初始为空
把regel应用于tupel上生成新的Tupel,然后循环
线性:
recursion分线性与非线性
如上述的regel即为线性的,他相应的非线性的regel为:
Ancestor(X,Y):-Parent(X,Y)
Ancestor(X,Y):-Ancestor(X,Z),Ancestor(Z,Y)
//没看出是怎么区分的???
有些系统不支持非线性的recursion
运行结束:
上述运行算法的在什么时候终结可以很明显的看出来,因为对于原始有限的n个tupel,那么他可以计算出他最多就能生成n(n+1)/2个Ancestor,因为有上限所有可以很好得识别出算法的结束
与Prolog的区别
Datalog的Regel的顺序无关紧要
Datalog不包含有非
Prolog例子:来自WikiPedia
gamble(X):-gotmeoney(X)
gamble(X):-gotcredit(X),NOT gotmeney(X)
cut-Operator:停止寻找替换,也就是说当找到一个匹配的规则后就不继续尝试其他规则
green cut:即当去掉第一个规则后,规则还是正确的
red cut:与green cut相反
prolog效率比较高,但是相对的也比较容易出现错误(fehleranfaelliger)
另外Datalog的Predicate的参数不能是复杂的计算如P(f(1),2)是不允许的
Datalog Programm的语义(Semantik)
//这节还在问人中 至今都木回复,主要不知道Modelltheoretisch和Beweistheoretisch是怎么区分的???
Monotone属性
Monotone属性即增大一个访问或Operator的input,不会导致输出的缩减。比如Diff Operator就是Monotone的,而与之相反selection就不是Monotone的
Datalog访问都有Monotone属性
Datalog的表达能力
去掉Rekursion的Datalog ≡ 去掉diff Operator的Relational Algebra
例如: σA=C(R)⇔R1(A,B,C):−R(C,B,C)
带有非操作的recursion
在recursion 中加入非Operator可以提高表达能力,但同时也带来了一些麻烦,比如他可能导致访问的振动 比如下面的例子//好具体啊???
P(X):−R(X),¬Q(X)
Q(X):−R(X),¬P(X)
假设初始R有一个Tupel{0}, P,Q为空,那么第一轮之后P,Q都含有一个Tupel {0},但是第二轮,根据规则P,Q中得Tupel {0}则都会被删去,如此反复。
因此在regel的躯干中使用非Operator时应该经过仔细的考虑。
//Wird negatives Liberal der Form ¬P in Regel benutzt, muss P bis dahin vollständig berechnet sein.??? S49
分层规则(Stratifiziertes Programm):
把规则根据其可表达性进行分层://再次好具体啊???
例如:
第一层:
T(X,Y):-R(X,Y)
T(X,Y):-R(X,Z),T(Z,Y)
第二层:
C(X,Y):−T(X,Y),¬S(X,Y)
//是把有非操作的和没非操作的分开吗??显然没这么简单啊??
//分层有什么作用也还没搞清楚
结构图:
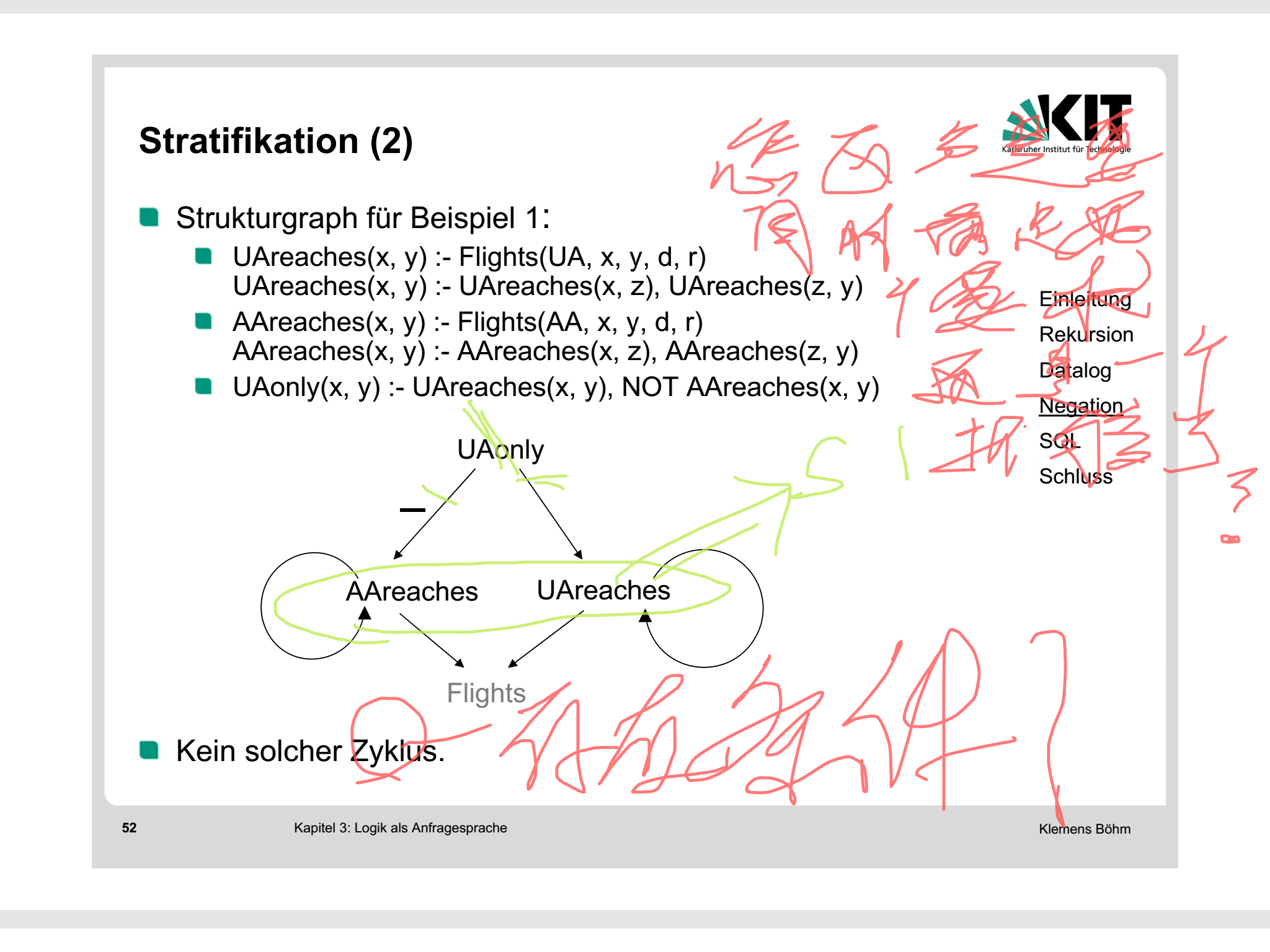
//这个还没经过老师的同意就上传了,算不算犯法啊
中间那个是上面规则的结构图,箭头表达了一种依赖关系,线上的“-”表示非Operator。
其中AAreaches和UAreaches为第一层规则,UAonly为第二层规则
一个正确的带有非Operator的Regel,他的结构图应该是不包含有循环的
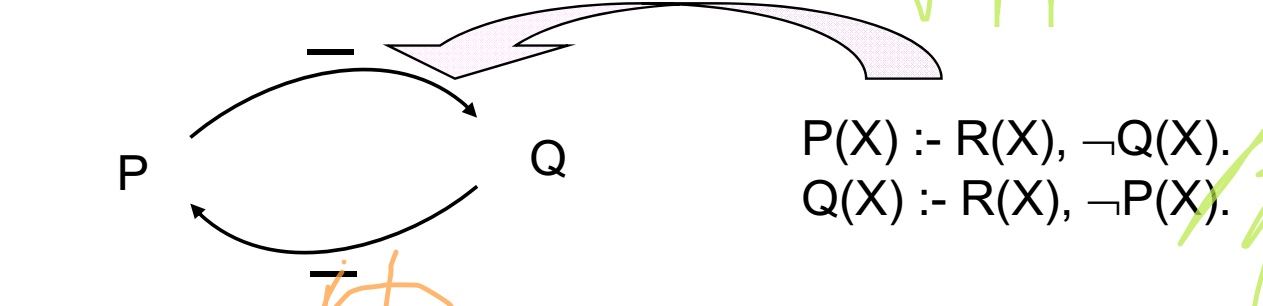
//这是反例!!!
检测结构图是否有循环的算法思想://不是一目了然吗??
删去第二层节点,和依赖于第二层节点的节点。//还剩下有第一层的几点就说明不含有循环吧??呵呵???
SQL中得recursion
SQL-99起允许在SQL访问中使用recursion
Datalog Programm:
Reaches(x,y):-Flights(a,x,y,d,r)
Reaches(x,y):-Reaches(x,z),Reaches(z,y)
SQL-99:
WITH RECURSIVE Reaches(from,to)AS
(SELECT arm,to FROM Flights)
UNION
(SELECT R1.arm,R2.to
FROM Reaches R1, Reaches R2
WHERE R1.to=R2.frm)
SELECT * FROM Reaches;
//其实这些语法不大懂,还得补习??
//另外还有Mutual Recursion也是不懂??S57
这篇关于数据库应用-Datalog的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







