LOOCV - Leave-One-Out-Cross-Validation 留一交叉验证

本文主要是介绍LOOCV - Leave-One-Out-Cross-Validation 留一交叉验证，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

什么是留一交叉验证

正常训练都会划分训练集和验证集，训练集用来训练模型，而验证集用来评估模型的泛化能力。留一交叉验证是一个极端的例子，如果数据集D的大小为N,那么用N-1条数据进行训练，用剩下的一条数据作为验证，用一条数据作为验证的坏处就是可能 $E_{val}$ 和 $E_{out}$ 相差很大，所以在留一交叉验证里，每次从D中取一组作为验证集，直到所有样本都作过验证集，共计算N次，最后对验证误差求平均，得到Eloocv(H,A)，这种方法称之为留一法交叉验证。
$\frac{1}{N}\sum_{n=1}^{N} e_{n} = \frac{1}{N}\sum_{n=1}^{N} err(g_{n}^{-}(x_{n}),y_{n})$

为什么使用LOOCV

至于为什么，其原因和为什么使用交叉验证是一样的，主要是为了防止过拟合，评估模型的泛化能力

什么时候使用LOOCV

当数据集D的数量较少时使用留一交叉验证，其原因主要如下

数据集少，如果像正常一样划分训练集和验证集进行训练，那么可以用于训练的数据本来就少，还被划分出去一部分，这样可以用来训练的数据就更少了。loocv可以充分的利用数据。
因为loocv需要划分N次，产生N批数据，所以在一轮训练中，要训练出N个模型，这样训练时间就大大增加。所以loocv比较适合训练集较少的场景

LOOCV理论证明

为什么可以使用LOOCV来近似估计泛化误差,即 $E_{loocv}\approx E_{out}$
证明如下
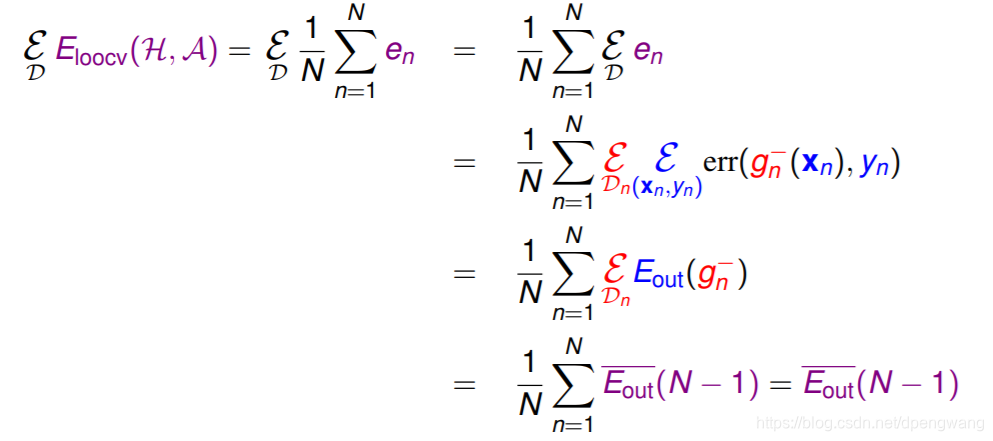
在这里插入图片描述

解释如下：

$\varepsilon_{D}$ 表示在不同数据集上的期望， $\varepsilon$ 是表示期望的符号，这里不同的数据D,我的理解是对原始数据的N次划分得到的不同数据集
$\varepsilon_{D}e_{n}$ => $\varepsilon_{D_{n}}\varepsilon_{{(x_{n},y_{n})}}e_{n}$ 是因为 $D_{n}$ 和 $x_{n},y_{n})$ 服从iid分布
$\varepsilon_{{(x_{n},y_{n})}}err(g_{n}^{-}(x_{n}),y_{n})$ 转化为 $E_{out}(g_{n}^{-})$ 是期望的定义和 $E_{out}$ 的定义，虽然是对剩下的一个求误差，但是求的是对剩下单个数据的期望，单个数据的的期望相当于对所有未知数据上求概率平均（因为训练数据和位置数据是iid,所以对训练数据求期望相当终于对未知数据求期望），也就是 $g_{n}^{-}$ 在未知数据上的E即 $E_{out}$

LOOCV的优点

充分利用数据
因为采样是确定的，所以最终误差也是确定的，不需要重复LOOCV

LOOCV的缺点

训练起来耗时
由于每次只采一个样本作为验证，导致无法分层抽样，影响验证集上的误差。举个例子，数据集中有数量相等的两个类，对于一条随机数据，他的预测结果是被预测为多数的结果，如果每次划出一条数据作为验证，则其对应的训练集中则会少一条，导致训练集中该条数据占少数从而被预测为相反的类，这样原来的误差率为50%，在LOOCV中为100%

LOOCV模型选择问题

之前有个疑问就是，在留一交叉验证过后，到底选择哪一个模型作为最终的模型呢？比如一百条数据在LOOCV中训练了一百个模型，选择其中最好的一个吗，其实不是这样的。
考虑一般的划分训练，train_data七三划分为训练集和验证集，然后每一轮训练都会得到一个 $E_{val}$ ，训练到 $E_{val}$ 最低为止，此时的模型就是最终的模型。
LOOCV也是这样的，只不过原来每一轮的训练对应于LOOCV中划分N次训练N个模型，原来的 $E_{val}$ 对应于LOOCV每一轮N个误差的平均，这样一轮轮下来直到验证集上的误差最小，此时的模型就是最终需要的模型（这个模型内部有N个小模型）