跳蚱蜢（蓝桥杯）

2024-03-25 13:28

文章标签 蓝桥蚱蜢

本文主要是介绍跳蚱蜢（蓝桥杯），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

跳蚱蜢
- 题目描述
- 答案：20
- bfs

跳蚱蜢

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

如下图所示：有 9 只盘子，排成 1 个圆圈。其中 8 只盘子内装着 8 只蚱蜢，有一个是空盘。我们把这些蚱蜢顺时针编号为 1 ~ 8。

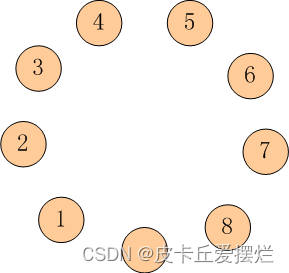
在这里插入图片描述

每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。

请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，并且保持空盘的位置不变（也就是 1-8 换位，2-7换位,…），至少要经过多少次跳跃？

答案：20

bfs

这段C++代码是用来解决一个特定的问题：计算把一系列编号为1至8的蚱蜢，从顺时针排列改为逆时针排列（在一个圆圈中，含有一个空盘），至少需要多少次跳跃。下面是对代码各部分的详细注释：

// 包含C++标准库，例如输入输出流、数据结构等
#include<bits/stdc++.h>
using namespace std;// 定义初始状态字符串和目标状态字符串
string st="123456780",ed="876543210";
// 使用哈希表来记录每个状态的最小跳跃次数
unordered_map<string,int> d;
// 使用队列来进行宽度优先搜索(BFS)
queue<string> q;
// 定义4种跳跃方式：向右跳1格、向左跳1格、向右跳2格越过一个蚱蜢、向左跳2格越过一个蚱蜢
int dx[4]={1,-1,2,-2};
// 定义总的盘子数量
int n=9;// 定义宽度优先搜索函数，用于找到从初始状态到目标状态的最少跳跃次数
int bfs()
{// 将初始状态入队，并将其跳跃次数设为0q.push(st);d[st]=0;// 当队列不为空时进行循环while(q.size()){// 从队列中取出一个状态auto t=q.front();q.pop();// 查找空盘的位置int k=t.find('0');// 试验四种跳跃方式for(int i=0;i<4;i++){// 创建一个新状态，作为当前状态的副本string str=t;// 尝试执行一次跳跃，注意取模操作是为了处理环形排列的情况swap(str[k],str[(k+dx[i]+9)%9]);// 如果新状态已经被访问过，则忽略if(d.count(str)) continue;// 否则，记录新状态的跳跃次数（当前状态的跳跃次数+1），并将新状态入队d[str]=d[t]+1;q.push(str);}}// 返回到达目标状态的最少跳跃次数return d[ed];
}int main()
{// 输出最少跳跃次数cout<<bfs()<<endl;return 0;
}