二叉树的遍历及线索二叉树试题解析

本文主要是介绍二叉树的遍历及线索二叉树试题解析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、单项选择题
01.在下列关于二叉树遍历的说法中，正确的是( C ).
A.若有一个结点是二叉树中某个子树的中序遍历结果序列的最后一个结点，则它一定是该子树的前序遍历结果序列的最后一个结点
B.若有一个结点是二叉树中某个子树的前序遍历结果序列的最后一个结点，则它一定是该子树的中序遍历结果序列的最后一个结点
C.若有一个叶结点是二叉树中某个子树的中序遍历结果序列的最后一个结点，则它一定是该子树的前序遍历结果序列的最后一个结点
D.若有一个叶结点是二叉树中某个子树的前序遍历结果序列的最后一个结点，则它一定是该子树的中序遍历结果序列的最后一个结点
解析：二叉树中序遍历的最后一个结点一定是从根开始沿右子女指针缝走到底的结点

02．在任何一棵二叉树中，若结点a有左孩子b、右孩子c，则在结点的先序序列、中序序列、后序序列中，(C ).
A.结点b一定在结点a的前面 B.结点a一定在结点c的前面
C.结点b一定在结点c的前面 D.结点a一定在结点b的前面
解析：三种遍历方式中，都先遍历左子树再遍历右子树

03.设n,m为一棵二叉树上的两个结点，在中序遍历时，n在m前的条件是（C )
A. n在m右方 B. n是m祖先 C. n在m左方 D. n是m子孙
解析:中序遍历时，先访问左子树再访问根结点，再访问右结点，m为根结点，n为左子树符合题意，n为左结点，m为右结点也符合题意，可知n都在m左方

04．设n,m为一棵二叉树上的两个结点，在后序遍历时，n在m前的充分条件是(D )
A. n在m右方 B. n是m祖先 C. n在m左方 D. n是m子孙
解析：后序遍历的顺序是左右根，只有m为根节点的情况下才能让n在前

05．在二叉树中有两个结点m和n，若m是n的祖先，则使用(C )可以找到从m到n的路径。
A.先序遍历 B.中序遍历 C.后序遍历 D.层次遍历
解析：在后序遍历退回时访问根结点，就可以从下向上把从n到m的路径上的结点输出，若采用非递归的算法，则当后序遍历访问到n时，栈中把从根到n的父指针的路径上的结点都记忆下来，也可以找到从m到n的路径。

06．某非空二叉树采用顺序存储结构，树中的结点信息按完全二叉树的层次序列依次存放在
如下所示的一维数组中，则该二叉树的后序遍历序列为( C ).

A. ghbefhca B. gbdehcfa C. gdbhefca D. bgdehcfa
解析：其图形如下所示：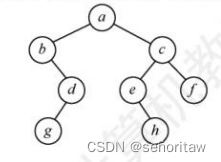

07．在二叉树的前序序列、中序序列和后序序列中，所有叶结点的先后顺序（B )
A.都不相同 B.完全相同 C．前序和中序相同，而与后序不同
D.中序和后序相同，而与前序不同
解析：三种遍历方式访问左右子树的先后顺序都是不变的，只是访问根节点的顺序不同

08．对二叉树的结点从1开始进行连续编号，要求每个结点的编号大于其左、右孩子的编号，
同一结点的左、右孩子中，其左孩子的编号小于其右孩子的编号，可采用（ C ）次序的遍历实现编号。
A.先序遍历 B.中序遍历 C.后序遍历 D.层次遍历
解析：从1开始编号，编号越大说明遍历顺序越靠后，左孩子编号小于右孩子编号，结点大于左右编号，所以遍历顺序为左右根，后序遍历

09.按某种顺序对二叉树的结点进行编号，编号为1,2,…,n，规定:树中任一结点v，其编
号等于v的左子树上的最小编号减1，而v的右子树中的最小编号等于v的左子树上的最大编号加1，则说明该二叉树是按（ B )次序编号的。
A．中序遍历 B.先序遍历 C．后序遍历 D．层次遍历
解析：结点v的编号比左子树的最小编号还小，而v的右子树中的最小编号又大于v的左子树中的最大编号，因此v的编号小于左右所有子树的编号，显然是从根节点按先序遍历

10.前序序列为A,B,C，后序序列为C, B,A 的二叉树共有（D )。
A.1棵 B.2棵 C.3棵 D.4棵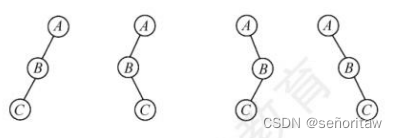

11.一棵完全二叉树的后序遍历序列为CDBFGEA，则其先序遍历序列是(C ).
A.CBDAFEG B. ABECDFG C. ABCDEFG D.无法确定
解析：画出七个结点的三层满二叉树再根据后序序列把值填入结点

12．设结点X和Y是二叉树中任意的两个结点。在该二叉树的先序遍历序列中X在Y之前，
而在其后序遍历序列中X在Y之后，则X和Y的关系是( C )。
A.X是Y的左兄弟 B.X是Y的右兄弟 C.X是Y的祖先 D.X是Y的后裔
解析：二叉树的先序遍历是根左右，后序遍历是左右根，则只有X为根，Y为左右子树满足题设

13．若二叉树中结点的先序序列是…a…b….，中序序列是….b…a…，则( C )。.
A.结点a和结点b分别在某结点的左子树和右子树中
B.结点b在结点a的右子树中
C.结点b在结点a的左子树中
D.结点a和结点b分别在某结点的两棵非空子树中
解析:根左右，左根右，只有一个为根一个为左子树才可能顺序相反，而先序a在前所以C对

14.一棵二叉树的先序遍历序列为1234567，它的中序遍历序列可能是（B)。.
A. 3124567 B.1234567 C.4135627 D.1463572
解析：排除法

15．下列序列中，不能唯一地确定一棵二叉树的是( D)。
A．层次序列和中序序列 B.先序序列和中序序列
C．后序序列和中序序列 D.先序序列和后序序列

16.若一棵二叉树的中序序列和后序序列相同，则( B )。
A.二叉树为空树或二叉树任一结点没有左子树
B.二叉树为空树或二叉树任一结点没有右子树
C.二叉树为空树或二叉树中每个结点的度为1
D.二叉树为空树或二叉树为满二叉树
解析:中序遍历是“左根右”,后序遍历是“左右根”，当任一结点没有右子树时，两种遍历都是“左根”，当二叉树为空或只有根节点时，中序序列和后序序列也相同

17.已知一棵二叉树的后序序列为DABEC，中序序列为DEBAC，则先序序列为(D )
A. ACBED B. DECAB C.DEABC D.CEDBA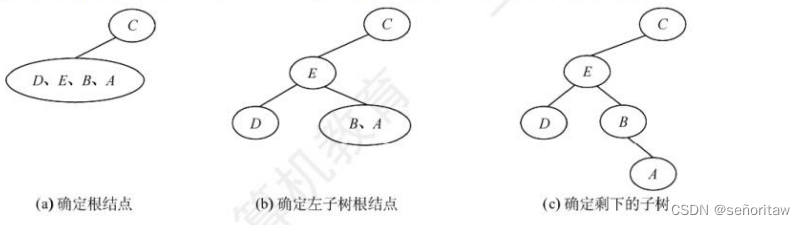

18.已知一棵二叉树的先序遍历结果为ABCDEF，中序遍历结果为CBAEDF，则后序遍历的
结果为（ A )。
A. CBEFDA B. FEDCBA C. CBEDFA D．不确定

19.已知一棵二叉树的层次序列为ABCDEF，中序序列为BADCFE，则先序序列为( B )。
A.ACBEDF B. ABCDEF C.BDFECA D.FCEDBA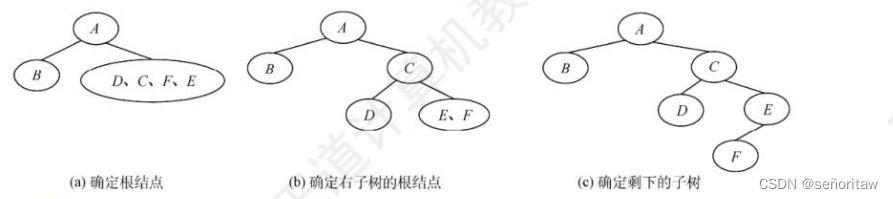

20.某二叉树中的结点x,它在先序、中序、后序遍历序列中的编号分别为pre(x) ,in (z)、post(x)（假设都是从1开始依次编号),a和b是树中任意两个结点，下列选项中错误的是( B )
A. a是b的后代且pre (a)<pre(b) B. a是b的祖先且post (a) >post (b)
C. a是b的后代且in (a)<in(b) D. a在b的左边且in (a)<in(b)
解析:若a是b的祖先，则后序遍历时一定先遍历b后遍历a

21.某二叉树采用二叉链表存储结构，若要删除该二叉链表中的所有结点，并释放它们占用
的存储空间，则采用( C )遍历方法最合适。
A.中序 B.层次 C.后序 D.先序
解析:删除一个结点时，需要先递归的删除它的左右孩子，并释放他们所占的内存空间，然后删除该结点，并删除它所占的存储空间，这正好与后续遍历的访问顺序相同

22.引入线索二叉树的目的是( A ).
A.加快查找结点的前驱或后继的速度 B.为了能在二叉树中方便插入和删除
C.为了能方便找到双亲 D.使二叉树的遍历结果唯一
解析：线索是前驱结点和后继结点的指针，引入线索的目的是加快对二叉树的遍历

23.线索二叉树是一种（ C )结构。
A.逻辑 B.逻辑和存储 C.物理 D.线性
解析：二叉树是一种逻辑结构，但线索二叉树是加上线索后的链表结构，即它是二叉树在计算机内部的一种存储结构，所以是一种物理结构

24. n个结点的线索二叉树上含有的线索数为( C )。
A. 2n B. n-l C. n+1 D. n
解析：n个结点共有链域指针2n个，其中除根结点外每个结点都被一个指针指向，剩余的链域建立线索，共有2n-(n-1)=n+1个线索

25．判断线索二叉树中*p结点有右孩子结点的条件是( C).
A. p !=NULL B.p->rchild !=NULL C. p->rtag==0 D. p->rtag==1
解析：线索二叉树中用ltag/rtag标识结点的左/右指针域是否为线索，其值为1时，对应指针域为线索，其值为0时，对应指针域为左右孩子

26.一棵左子树为空的二叉树在先序线索化后，其中空的链域的个数是( D ).
A．不确定 B.0个 C. 1个 D.2个
解析：对左子树为空的二叉树进行先序线索化，根结点的左子树为空并且没有前驱结点(先遍历根结点)，先序遍历的最后一个元素做为叶结点，左、右子树均为空且有前驱无后继结点，所以线索化后，树中空链域有两个

27．在线索二叉树中，下列说法不正确的是( D)。
A.在中序线索树中，若某结点有右孩子，则其后继结点是它的右子树的最左下结点
B.在中序线索树中，若某结点有左孩子，则其前驱结点是它的左子树的最右下结点
C.线索二叉树是利用二叉树的n+1个空指针来存放结点的前驱和后继信息的
D.每个结点通过线索都可以直接找到它的前驱和后继
解析：不是每个结点通过线索都可以直接找到它的前驱和后继。在先序线索二叉树中查找一个结点的先序后继很简单，而查找先序前驱必须知道该结点的双亲结点。同样，在后序线索二叉树中查找一个结点的后序前驱也很简单，而查找后序后继也必须知道该结点的双亲结点，二叉链表中没有存放双亲的指针。

28.二叉树在线索化后，仍不能有效求解的问题是( D ) 。
A.先序线索二叉树中求先序后继
B.中序线索二叉树中求中序后继
C.中序线索二叉树中求中序前驱
D.后序线索二叉树中求后序后继
解析：后序线索二叉树不能有效解决求后序后继的问题。如下图所示，结点E的右指针指向右孩子，而在后序序列中E的后继结点为B，在查找E的后继时仍然只能按常规方法来查找。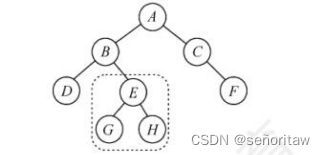

29.若X是二叉中序线索树中一个有左孩子的结点，且X不为根，则X的前驱为( C )。
A.X的双亲 B.X的右子树中最左的结点
C.X的左子树中最右的结点 D.X的左子树中最右的叶结点
解析：在二叉树中序线索树种，某结点若有左孩子，按照中序“左根右”的顺序，该结点的前驱结点为左子树中最右的一个结点

30.若X是后序线索二叉树中的叶结点，且X存在左兄弟Y，则X的右线索指向的是(A )。
A.X的双亲 B.以Y为根的子树的最左下结点
C.X的左兄弟Y D.以y为根的子树的最右下结点

31.(C)的遍历仍需要栈的支持。
A.前序线索树 B.中序线索树 C．后序线索树 D.所有线索树
解析：后序线索树遍历时，最后访问根结点，若从右孩子x返回访问父结点，则由于结点x的右孩子不一定为空（右指针无法指向其后继)，因此通过指针可能无法遍历整棵树。如下图所示，结点中的数字表示遍历的顺序，图(c)中结点6的右指针指向其右孩子5，而不指向其后序后继结点7，因此后序遍历还需要栈的支持，而图(a)和图(b)均可遍历。

32.某二叉树的先序序列和后序序列正好相反，则该二叉树一定是( B )。
A.空或只有一个结点 B.高度等于其结点数
C.任意一个结点无左孩子 D.任意一个结点无右孩子
解析：非空二叉树的先序序列和后序序列相反，即“根左右”与“左右根”顺序相反，因此树只有根结点，或根结点只有左子树或右子树，其子树也有同样的性质，任意结点只有一个孩子，才能满足先序序列和后序序列正好相反。此时树形应为一个长链，树中仅有一个叶结点。

33.【2009统考真题】给定二叉树如下图所示。设N代表二叉树的根，L代表根结点的左子
树，R代表根结点的右子树。若遍历后的结点序列是3175624，则其遍历方式是( D )。

A.LRN B.NRL C.RLN D.RNL
解析:分析遍历后的结点序列,可以看出根结点是在中间被访问的,而且右子树结点在左子树之前，则遍历的方法是RNL。

34.【2010统考真题】下列线索二叉树中(用虚线表示线索)，符合后序线索树定义的是( D )。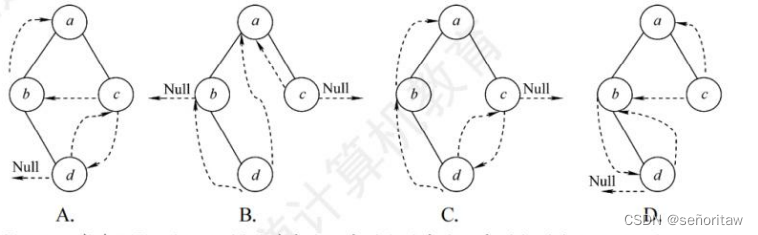

解析：暂未分析

35.【2011统考真题】一棵二叉树的前序遍历序列和后序遍历序列分别为1,2,3,4和4,3,2,1，
该二叉树的中序遍历序列不会是( C ).
A. 1,2,3,4 B. 2,3,4,1 C. 3,2,4,1 D.4,3,2,1
解析：ABD的图像都满足题设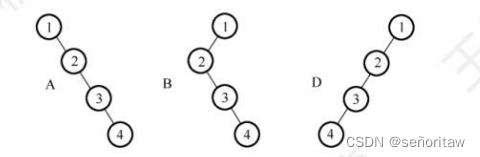

36.【2012统考真题】若一棵二叉树的前序遍历序列为a, e, b,d, c，后序遍历序列为b, c, d, e,
a，则根结点的孩子结点( A ).
A.只有e B.有e、b C.有e、c D.无法确定
解析：前序遍历和后序遍历不能唯一确定一颗二叉树，但是可以确定二叉树的祖先关系由前序后序可知a是根结点，e为a的孩子结点，此外由a的孩子结点组成的前序序列为ebd、后序序列为bcde,可知e是bcd的祖先，所以根结点的孩子结点只有e

37.【2013统考真题】若X是后序线索二叉树中的叶结点，且X存在左兄弟结点Y，则X的
右线索指向的是( A ).
A.X的父结点 B.以Y为根的子树的最左下结点
C.X的左兄弟结点Y D.以Y为根的子树的最右下结点
解析：X是叶结点且存在左兄弟结点Y,则X是根节点的右结点，后序遍历方式左右根，可知X结点的后序后继是其父结点，即右线索指向的是父结点

38.【2014统考真题】若对下图所示的二叉树进行中序线索化，则结点X的左、右线索指向
的结点分别是（ D )。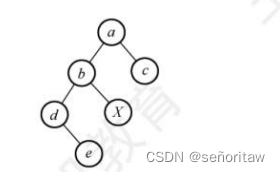

A. e, c B.e, a C. d, c D. b, a
解析：线索二叉树的线索实际指向的是相应遍历序列特点结点的前驱结点和后继结点，图中中序遍历序列为debxac ,x左边和右边的字符分别对应左右线索

39.【2015统考真题】先序序列为a, b, c, d的不同二叉树的个数是( B).
A.13 B.14 C. 15 D.16
解析：

40.【2017统考真题】某二叉树的树形如下图所示，其后序序列为e,a, c, b, d,g,f，树中与结
点a同层的结点是( B )。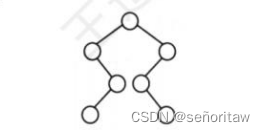

A. c B. d C. f D.g
解析：后序序列访问顺序为左右根，递归进行，根节点的左子树e最先被访问，由于没有右子树接下来访问的是父结点a,然后是a的父结点c,接着访问右子树，由于右子树有根结点所以先访问根结点b,再访问根结点的父结点d,然后是d的结点g,最后是根节点f,最后如下图所示，与a同层的结点为d

41.【2017统考真题】要使一棵非空二叉树的先序序列与中序序列相同，其所有非叶结点须
满足的条件是( B).
A.只有左子树 B.只有右子树 C.结点的度均为1 D.结点的度均为2
解析：先序序列访问顺序为根左右、中序序列访问为左根右，若非叶结点只有右子树，则先序序列和中序序列都先访问父结点，后访问右子树

42.【2022统考真题】若结点p与q在二叉树T的中序遍历序列中相邻，且p在q之前，则下列p与q的关系中，不可能的是( B )。
Ⅰ.q是p的双亲
Ⅱ.q是p的右孩子
Ⅲ.q是p的右兄弟
IV.q是p的双亲的双亲
A.仅I B.仅Ⅲ C.仅Ⅱ、Ⅲ D.仅Ⅱ、IV
解析：中序遍历的访问顺序是左根右，Ⅲ，q是p的右兄弟，但中序遍历先遍历左结点再遍历根结点，不可能跟右结点相邻

43.【2023统考真题】已知一棵二叉树的树形如下图所示，若其后序遍历序列为fdbeca，则其
先(前)序遍历序列是( A )。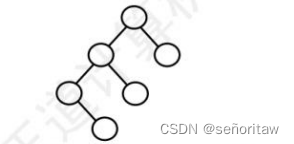

A. aedfbc B. acebdf C. cabefad D. dfebac