202305 CSP认证

本文主要是介绍202305 CSP认证，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

202305-1 重复局面
第一题直接干

#include<bits/stdc++.h>
using namespace std;
unordered_map<string, int> chess;
int main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);string line, str = ""; int n;cin >> n;while(n --){str = "";for(int i = 0;i < 8;i ++){cin >> line;str += line;}if(!chess.count(str)) chess[str] = 0;chess[str] ++;cout << chess[str] << endl;}return 0;
}

202305-2 矩阵运算
这道题算是我近几年来唯一一道还没有做的第二题，当时没做是觉得肯定会超时

其实考察的就是一个简单的算法知识，如何处理矩阵乘法。
假设矩阵A(m * n) 和 B(n * m)相乘，则其时间复杂度O(n) = m * n * m
也就是如果本题按照它所给的矩阵乘法顺序计算的话，时间复杂度是n * d * n会超时，所以这里改变矩阵运算的顺序即可。不要被点乘迷晕了以为不能替换，它给的式子是个变体，原型是：
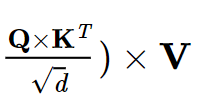
在这里插入图片描述

这个式子就很明显上面三个矩阵运算的顺序其实是把括号打在左二和右二都是可以的，引入W点乘其实就是除以一个常数的作用而已，不用纠结

最后提交的满分结果如下：

在这里插入图片描述

满分代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e4 + 10;
const int D = 25;
int Q[N][D], KT[D][N], V[N][D], W[N];
int main()
{ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);int n, d; cin >> n >> d;for(int i = 0;i < n;i ++)for(int j = 0;j < d;j ++)cin >> Q[i][j];for(int j = 0;j < n;j ++)for(int i = 0;i < d;i ++)   //这里容易出错 KT的大小是d x n, 始终用(i,j)表示数组中的元素cin >> KT[i][j]; for(int i = 0;i < n;i ++)for(int j = 0;j < d;j ++)cin >> V[i][j];for(int i = 0;i < n;i ++)cin >> W[i];//矩阵乘法 KT(dn) x V(nd)  O(n) = nddll temp1[D][D];for(int i = 0;i < d;i ++){for(int j = 0;j < d;j ++){//(i,j) 是KT的第i行乘V的第j列的和ll sum = 0;for(int u = 0;u < n; u ++){sum += (KT[i][u] * V[u][j]);}temp1[i][j] = sum;}}//矩阵乘法Q(nd) x temp1(dd) O(n) = nddll temp2[N][D];for(int i = 0;i < n;i ++){for(int j = 0;j < d;j ++){ll ans = 0;for(int u = 0;u < d;u ++){ans += (Q[i][u] * temp1[u][j]);}temp2[i][j] = ans;}}//计算点乘for(int i = 0;i < n;i ++){for(int j = 0;j < d;j ++){temp2[i][j] *= W[i];}}for(int i = 0;i < n;i ++){for(int j = 0;j < d;j ++){cout << temp2[i][j] << " ";}cout << endl;}return 0;
}

OK顺利步入第三题
这道题目我记得我第一遍看的时候就因为审题没有看明白就完全放弃了。

题目看起来很复杂！但无论如何在考场上都要静下心去读题！
本题考察的就是位运算。对于输入的一些字节流（每两个字符视作一个字节），按照题目所给的条件进行运算。

先解释一下题目吧。我觉得在这里要明确一点，题目明确说了给的输入一定是合法的！！！所以不用去纠结判断的事情，这样会让思路更加混乱。基于这一点，引导区的内容可以直接忽略，因为我们只需要解码数据区即可，而且只要保证解码过程中的代码逻辑准确，就不会有差错

本题看似有非常多的字符，但是在合法的前提下，我们其实只需要对首字节做判断。
判断的第一个就是针对于低两位，我们可以直接用位运算实现，也就是num & 3

如果首字节的低两位是00：此时代表字面量。很简单不要害怕！！针对高六位再次判断，在某个数值范围内直接得到l；在另外一个数值范围内需要额外读到下面的一个字节，计数就好啦！！
如果首字节的低两位是01：回溯。按照题目所给操作进行即可
如果首字节的低两位是10：回溯。按照题目所给操作进行即可
不可能有11的低两位！保证输入合法

其实操作的实现全都依赖于位运算

>> & <<：这个很常用。比方说在本题中，首字节的低两位只涉及到类型，在和3在按位与之后低两位是没用的，此时我直接移位，num >>= 2，只保留高六位即可；还有高三位和下一个输入的字节的八位组合成一个数字的时候，也采用了移位操作
&：按位与操作可以保留对应数位，因为1 & 1 = 1,0 & 1 = 0.也就是说和1做与运算是可以保留当前位的

本题难度其实真的不大，重点在看懂题目以及明白C++中的位运算
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;int s;           //输入的字节数
char bit4[2];   //两个字符构成一个字节,这里用一个字符数组来存储一个字节
int k = 0;     //用来计数换行的
string str = "";    //用来存储已经输出的字符，用于回溯//将一个字符转化为十进制数
int trans_10(char ch)
{if(ch >= '0' && ch <= '9') return ch - '0';if(ch >= 'a' && ch <= 'f') return ch - 'a' + 10;
}
//打印字面量
void Print(int l)
{while(l --){cin >> bit4[0] >> bit4[1]; s --;str += bit4[0], str += bit4[1];cout << bit4[0] << bit4[1];k ++;if(k == 8) { cout << endl; k = 0; }}
}
void trace(int o, int l)
{cout <<"\no："<<o<<"l:"<<l<<endl;int sz = str.size();int pos = sz - 2 * o;   //定位一个开始点while(l > 0){   //必须输出L个字节for(int i = pos; i < sz && l > 0; i += 2, l --){cout << str[i] << str[i + 1];k ++;if(k == 8) { cout << endl; k = 0; }str += str[i], str += str[i + 1];   //这个容易漏}}
}
int main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cin >> s;while(s){cin >> bit4[0] >> bit4[1]; s --;if(!(trans_10(bit4[0]) & 8)) break;   //如果最高位为0,引导区结束}while(s){cin >> bit4[0] >> bit4[1]; s --; //首字节cout << "\n当前的首字节是"<<bit4[0]<<bit4[1]<<endl;int a = trans_10(bit4[0]), b = trans_10(bit4[1]);int num = (a << 4) + b;   //将字节转化为10进制数字int type = num & 3;   //取出后两位num >>= 2;       //只保留高六位if(type == 0){   //为字面量int l = 0;if(num <= 59) l = num + 1;else{int cnt = num - 59;   //需要向后读取cnt个字节for(int i = 0;i < cnt;i ++){cin >> bit4[0] >> bit4[1]; s --;a = trans_10(bit4[0]), b = trans_10(bit4[1]);l += ( ((a << 4) + b) << (8 * i) );//得到当前字节表示的数后，由于是小端序，需要进行相应的移位(以8位，也就是一个字节为单位)}l ++;}Print(l);}else if(type == 1){int l = num & 7;  //取后三位l += 4;num >>= 3;int o = (num << 8);cin >> bit4[0] >> bit4[1]; s --;a = trans_10(bit4[0]), b = trans_10(bit4[1]);o += ((a << 4) + b);trace(o, l);}else{int l = num + 1;int o = 0;for(int i = 0;i < 2;i ++){cin >> bit4[0] >> bit4[1]; s --;a = trans_10(bit4[0]), b = trans_10(bit4[1]);o += ( ((a << 4) + b) << (8 * i) );}trace(o, l);}}return 0;
}