matlab vdp函数,MATLAB第29讲

利用泛函命令进行数值分析

在MATLAB中，所有以函数为输入变量的命令，都称为泛函命令。

常见语法：

[输出变量列表]=函数名(h_fun,输入变量列表)

[输出变量列表]=函数名('funname',输入变量列表)

说明：h_fun是要被执行的M函数文件的句柄，或者是内联函数和字符串；'funname'是M函数文件名。

1．fminbnd函数

fminbnd函数用来计算单变量非线性函数的极小值。

[x,y]=fminbnd(h_fun,x1,x2,options)

[x,y]=fminbnd('funname',x1,x2,options)

说明：h_fun是函数句柄，'funname'是函数名，必须是单值非线性函数；options是用来控制算法的参数向量，默认值为0，可省略；x是fun函数在区间x1

【例5.22】  用fminbnd求解humps函数的极小值。

>>[x,y]=fminbnd(@humps,0.5,0.8)

%求在0.5～0.8之间的极小值

程序分析：humps函数是MATLAB提供的M文件，保存为humps.m文件；@humps表示humps函数的句柄，humps的函数最小值曲线如图所示，最小值为图中的圆点(0.6370，11.2528)，误差小于10-4。

2．fminsearch函数

fminsearch函数用于求多变量无束缚非线性最小值，采用Nelder-Mead单纯形算法求解多变量函数的最小值。

x=fminsearch(h_fun,x0)

x=fminsearch('funname',x0)

说明：x0是最小值点的初始猜测值。

【例5.23】  求著名的Banana测试函数f(x,y)=100(y-x2)2+(1-x)2的最小值，它的理论最小值是x=1，y=1。该测试函数有一片浅谷，很多算法都难以逾越。

>>fn=inline('100*(x(2) -x(1)^2)^2+(1-x(1))^2','x')

%用inline产生内联函数，x和y用二元数组表示

Inline function:

fn(x)=100*(x(2) -x(1)^2)^2+(1-x(1))^2

>>y=fminsearch(fn,[0.5, -1])

%从(0.5,-1)为初始值开始搜索求最小值

1.0000  1.0000

fzero函数可以寻找一维函数的零点，即求f(x)=0的根。

x=fzero(h_fun,x0,tol,trace)

x=fzero('funname',x0,tol,trace)

说明：h_fun是待求零点的函数句柄；x0有2个作用：预定待搜索零点的大致位置和搜索起始点；tol用来控制结果的相对精度，默认值为eps；trace指定迭代信息是否在运算中显示，默认为0，表示不显示迭代信息。tol和trace都可以省略。

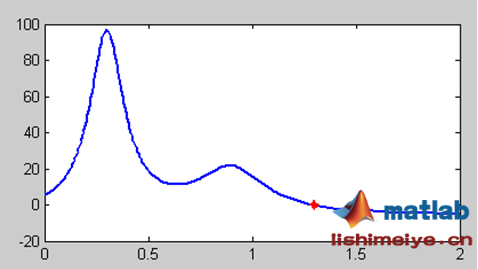
【例5.24】求解humps函数的过零点，humps函数的过零点用圆点表示，如图所示。

>>xzero=fzero(@humps,1)

%求在1附近的零点

>>xzero=fzero(@humps,[0.5,1.5])

%求在0.5～1.5范围内的零点

>>xzero=fzero(@humps,[0.5,1])

%求在0.5～1范围内的零点

???Errorusing==>fzero

The

function valuesat the

interval end points must differinsign.

函数quad和quad8基于数学上的正方形概念计算函数的面积。这2个函数在所需的区间计算被积函数都应用递归调用的方法，quad8比quad更精确，速度更快。与trapz梯形比较这2个函数能够进行更高阶的近似。

s=quad(h_fun,x1,x2,tol,trace,p1,p2,…)

s=quad('funname',x1,x2,tol,trace,p1,p2,…)

s=quad8(h_fun,x1,x2,tol,trace,p1,p2,…)

s=quad8('funname',x1,x2,tol,trace,p1,p2,…)

【例5.25】  计算y=humps(x)曲线下面的面积。

>>x=0:0.01:1;

>>y=humps(x);

>>area=trapz(x,y)  %用梯形计算积分

>>area1=quad(@humps,0,1)  %用quad计算积分

>>area2=quad8(@humps,0,1)  %用quad8计算积分

MATLAB提供了ode23、ode45和ode113等多个函数求解微分方程的数值解。以下介绍低维方法、高维方法和变维方法解一阶常微方程组。

[t,y]=ode45(h_fun,tspan,y0,options,p1,p2…)

[t,y]=ode45('funname',tspan,y0,options,p1,p2…)

说明：h_fun是函数句柄，函数以dx为输出，以t，y为输入量；tspan=[起始值 终止值]，表示积分的起始值和终止值；y0是初始状态列向量；options可以定义函数运行时的参数，可省略；p1，p2…是函数的输入参数，可省略。

一般来说，ode45求解算法最常用。ode23和ode45都运用了基本的龙格－库塔(Runge-Kutta)数值积分法的变形，ode23运用组合2/3阶龙格－库塔法，而ode45运用组合的4/5阶龙格－库塔法，ode45可取较多的时间步。

函数M文件vdpol.m：

%范德波尔方程

Function

y prime=vdpol(t,y)

yprime=[y(2);2*(1-y(1)^2)*y(2)-y(1)]

(3)给定当前时间及y1和y2的初始值，解微分方程。

>>tspan=[0,30];  %起始值0和终止值30

>>y0=[1;0];  %初始值

>>[t,y]=ode45(@vdpol,tspan,y0);

%解微分方程

>>y1=y(:,1);

>>y2=y(:,2);

>>figure(1)

>>plot(t,y1,':b',t,y2,'-r')

%画微分方程解

>>figure(2)

>>plot(y1,y2)  %画相平面图