Codeforces Round #292 (Div. 2 Div. 1)

本文主要是介绍Codeforces Round #292 (Div. 2 Div. 1)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

比赛链接：http://codeforces.com/contest/515 http://codeforces.com/contest/516

Someday, Drazil wanted to go on date with Varda. Drazil and Varda live on Cartesian plane. Drazil's home is located in point(0, 0) and Varda's home is located in point(a, b). In each step, he can move in a unit distance in horizontal or vertical direction. In other words, from position(x, y) he can go to positions(x + 1, y),(x - 1, y),(x, y + 1) or(x, y - 1).

Unfortunately, Drazil doesn't have sense of direction. So he randomly chooses the direction he will go to in each step. He may accidentally return back to his house during his travel. Drazil may even not notice that he has arrived to (a, b) and continue travelling.

Luckily, Drazil arrived to the position (a, b) successfully. Drazil said to Varda: "It took me exactlys steps to travel from my house to yours". But Varda is confused about his words, she is not sure that it is possible to get from(0, 0) to (a, b) in exactlys steps. Can you find out if it is possible for Varda?

Input

You are given three integers a, b, and s ( - 10⁹ ≤ a, b ≤ 10⁹,1 ≤ s ≤ 2·10⁹) in a single line.

Output

If you think Drazil made a mistake and it is impossible to take exactlys steps and get from his home to Varda's home, print "No" (without quotes).

Otherwise, print "Yes".

Sample test(s)

Input

5 5 11

Output

No

Input

10 15 25

Output

Yes

Input

0 5 1

Output

No

Input

0 0 2

Output

Yes

Note

In fourth sample case one possible route is: 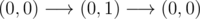$\text{[math]}$ .

题目大意：判断从原点(0,0)走整整s步有没有可能到点(a,b)

题目分析：坐标可能是负的，先把曼哈顿距离算出来，a + b > s不可能， a + b - s是2的倍数可能，否则不可能

#include <cstdio>int main()
{int a, b, s;scanf("%d %d %d", &a, &b, &s);if(a < 0)a = -a;if(b < 0)b = -b;if(a + b > s){printf("No\n");return 0;}if(a + b <= s && (a + b - s) % 2 == 0)printf("Yes\n");else printf("No\n");
}

Drazil has many friends. Some of them are happy and some of them are unhappy. Drazil wants to make all his friends become happy. So he invented the following plan.

There are n boys andm girls among his friends. Let's number them from0 ton - 1 and0 tom - 1 separately. Ini-th day, Drazil invites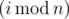 $\text{[math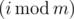]}$ -th boy and $\text{[math]}$ -th girl to have dinner together (as Drazil is programmer,i starts from0). If one of those two people is happy, the other one will also become happy. Otherwise, those two people remain in their states. Once a person becomes happy (or if he/she was happy originally), he stays happy forever.

Drazil wants to know whether he can use this plan to make all his friends become happy at some moment.

Input

The first line contains two integer n and m (1 ≤ n, m ≤ 100).

The second line contains integer b (0 ≤ b ≤ n), denoting the number of happy boys among friends of Drazil, and then followb distinct integersx₁, x₂, ..., x_b (0 ≤ x_i < n), denoting the list of indices of happy boys.

The third line conatins integer g (0 ≤ g ≤ m), denoting the number of happy girls among friends of Drazil, and then followg distinct integersy₁, y₂, ... , y_g (0 ≤ y_j < m), denoting the list of indices of happy girls.

It is guaranteed that there is at least one person that is unhappy among his friends.

Output

If Drazil can make all his friends become happy by this plan, print "Yes". Otherwise, print "No".

Sample test(s)

Input

2 3
0
1 0

Output

Yes

Input

2 4
1 0
1 2

Output

No

Input

2 3
1 0
1 1

Output

Yes

Note

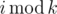By $\text{[math]}$ we define the remainder of integer division ofi byk.

In first sample case:

On the 0-th day, Drazil invites 0-th boy and 0-th girl. Because 0-th girl is happy at the beginning, 0-th boy become happy at this day.
On the 1-st day, Drazil invites 1-st boy and 1-st girl. They are both unhappy, so nothing changes at this day.
On the 2-nd day, Drazil invites 0-th boy and 2-nd girl. Because 0-th boy is already happy he makes 2-nd girl become happy at this day.
On the 3-rd day, Drazil invites 1-st boy and 0-th girl. 0-th girl is happy, so she makes 1-st boy happy.
On the 4-th day, Drazil invites 0-th boy and 1-st girl. 0-th boy is happy, so he makes the 1-st girl happy. So, all friends become happy at this moment.

题目大意：n个男生，m个女生，有b个男生x1 x2...xb一开始就是快乐的，其他是不快乐的，有g个女生y1 y2...yb一开始就是快乐的，其他是不快乐的，主人第i天邀请第i mod n个男生和第i mod m个女生参加聚会，两个人只要一个是快乐的另一个也会变快乐，问主人可不可能让所有人都快乐

题目分析：数据量不大，暴力模拟一下即可

#include <cstdio>
#include <cstring>
int const MAX = 105;
bool g[MAX], b[MAX];
int main()
{int n, m;scanf("%d %d", &n, &m);memset(g, false, sizeof(g));memset(b, false, sizeof(b));int hb, boy;scanf("%d", &hb);for(int i = 0; i < hb; i++){scanf("%d", &boy);b[boy] = true;}int hg, girl;scanf("%d", &hg);for(int i = 0; i < hg; i++){scanf("%d", &girl);g[girl] = true;}for(int i = 0; i < 100000; i++)if(b[i % n] || g[i % m])b[i % n] = g[i % m] = true;bool flag = true;for(int i = 0; i < n; i++){if(!b[i]){flag = false;break;}}for(int i = 0; i < m; i++){if(!g[i]){flag = false;break;}}printf("%s\n", flag ? "Yes" : "No");
}

Drazil is playing a math game with Varda.

Let's define 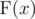$\text{[math]}$ for positive integerx as a product of factorials of its digits. For example, $\text{[math]}$ .

First, they choose a decimal number a consisting ofn digits that contains at least one digit larger than1. This number may possibly start with leading zeroes. Then they should find maximum positive numberx satisfying following two conditions:

1. x doesn't contain neither digit 0 nor digit 1.

2. $\text{[math]}$ = $\text{[math]}$ .

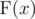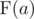Help friends find such number.

Input

The first line contains an integer n (1 ≤ n ≤ 15) — the number of digits ina.

The second line contains n digits of a. There is at least one digit in a that is larger than1. Numbera may possibly contain leading zeroes.

Output

Output a maximum possible integer satisfying the conditions above. There should be no zeroes and ones in this number decimal representation.

Sample test(s)

Input

4
1234

Output

Input

3
555

Output

Note

In the first case, $\text{[math]}$

题目大意：定义F1(x1x2x3...xn) = (x1)! * (x2)! * ... * (xn)!，现要求另一组F2(y1y2...ym)在满足F2==F1且 F2中没有0和1条件下，序列y1y2...ym的最大值

题目分析：推算出以下关系后，整理排序即可

0,1 delete
2！＝ 2！
3！＝ 3！
4！＝ 3！* 2！* 2！
5！＝ 5！
6！＝ 5！* 3！
7！＝ 7！
8！＝ 7！* 2！* 2！* 2！
9！＝ 7！* 3！* 3！* 2！

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
char s[20], ans[100000];bool cmp(char a, char b)
{return a > b;
}int main()
{int n;scanf("%d %s", &n, s);for(int i = 0; i < n; i++){if(s[i] == '2' || s[i] == '3' || s[i] == '5' || s[i] == '7'){int tmp = strlen(ans);ans[tmp++] = s[i];}else if(s[i] == '4')strcat(ans, "322");else if(s[i] == '6')strcat(ans, "53");else if(s[i] == '8')strcat(ans, "7222");else if(s[i] == '9')strcat(ans, "7332");}sort(ans, ans + strlen(ans), cmp);printf("%s\n", ans);
}

Drazil created a following problem about putting 1 × 2 tiles into an n × m grid:

"There is a grid with some cells that are empty and some cells that are occupied. You should use1 × 2 tiles to cover all empty cells and no two tiles should cover each other. And you should print a solution about how to do it."

But Drazil doesn't like to write special checking program for this task. His friend, Varda advised him: "how about asking contestant only to print the solutionwhen it exists and it is unique? Otherwise contestant may print 'Not unique' ".

Drazil found that the constraints for this task may be much larger than for the original task!

Can you solve this new problem?

Note that you should print 'Not unique' either when there exists no solution or when there exists several different solutions for the original task.

Input

The first line contains two integers n and m (1 ≤ n, m ≤ 2000).

The following n lines describe the grid rows. Character '.' denotes an empty cell, and the character '*' denotes a cell that is occupied.

Output

If there is no solution or the solution is not unique, you should print the string "Not unique".

Otherwise you should print how to cover all empty cells with1 × 2 tiles. Use characters "<>" to denote horizontal tiles and characters "^v" to denote vertical tiles. Refer to the sample test for the output format example.

Sample test(s)

Input

3 3
...
.*.
...

Output

Not unique

Input

4 4
..**
*...
*.**
....

Output

<>**
*^<>
*v**
<><>

Input

2 4
*..*
....

Output

*<>*
<><>

Input

1 1
.

Output

Not unique

Input

1 1
*

Output

Note

In the first case, there are indeed two solutions:

<>^
^*v
v<>

and

^<>
v*^
<>v

so the answer is "Not unique".

题目大意：n*m的矩阵，' . '表示位置空，' * '表示障碍物，问能不能用尖括号填满空的点，使矩阵中所有的尖括号都两两配对，水平配对：<> 竖直配对：^v，若不存在或答案不唯一输出Not unique

题目分析：有趣的题，DFS搜索，策略：先把*的点的数量记下来，每次向四周扩展时先找只有一个方向可扩展的点扩展，因为它的灵活度最小，也就是说在它这的策略是唯一的，每个点都搜一次，最后如果n * m = cnt表示每个点都填满了（包括障碍物）则说明有且只有一解

#include <cstdio>
#include <cstring>
int const MAX = 2005;
char s[MAX][MAX];
int n, m, cnt;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};void dfs(int x, int y)
{if(x < 1 || x > n || y < 1 || y > m || s[x][y] != '.')return;int dir = -1, sum = 0;for(int i = 0; i < 4; i++){int xx = x + dx[i];int yy = y + dy[i];if(s[xx][yy] == '.'){sum ++;dir = i;}}if(sum == 1)  //保证解的唯一性{if(dir == 0){s[x][y] = '<';s[x][y + 1] = '>';}else if(dir == 1){s[x][y] = '>';s[x][y - 1] = '<';}else if(dir == 2){s[x][y] = '^';s[x + 1][y] = 'v';}else if(dir == 3){s[x][y] = 'v';s[x - 1][y] = '^';}cnt += 2;for(int i = 0; i < 4; i++)dfs(x + dx[dir] + dx[i], y + dy[dir] + dy[i]);}
}int main()
{cnt = 0;scanf("%d %d", &n, &m);for(int i = 1; i <= n; i++)scanf("%s", s[i] + 1);for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)if(s[i][j] == '*')cnt ++;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)dfs(i, j);if(cnt == n * m)for(int i = 1; i <= n; i++)printf("%s\n", s[i] + 1);elseprintf("Not unique\n");
}

这篇关于Codeforces Round #292 (Div. 2 Div. 1)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！