本文主要是介绍Codeforces Round #320 (Div. 2) [Bayan Thanks-Round] (ABCDE题解)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
比赛链接：http://codeforces.com/contest/579
You are a lover of bacteria. You want to raise some bacteria in a box.
Initially, the box is empty. Each morning, you can put any number of bacteria into the box. And each night, every bacterium in the box will split into two bacteria. You hope to see exactly x bacteria in the box at some moment.
What is the minimum number of bacteria you need to put into the box across those days?
The only line containing one integer x (1 ≤ x ≤ 109).
The only line containing one integer: the answer.
5
2
8
1
For the first sample, we can add one bacterium in the box in the first day morning and at the third morning there will be 4 bacteria in the box. Now we put one more resulting 5 in the box. We added 2 bacteria in the process so the answer is 2.
For the second sample, we can put one in the first morning and in the 4-th morning there will be 8 in the box. So the answer is 1.
题目大意：求x的二进制表示里有几个1
题目分析：位运算
#include <cstdio>int main()
{int x, cnt = 0;scanf("%d", &x);while(x){if(x & 1)cnt ++;x >>= 1;}printf("%d\n", cnt);
}
There is a programing contest named SnakeUp, 2n people want to compete for it. In order to attend this contest, people need to form teams of exactly two people. You are given the strength of each possible combination of two people. All the values of the strengths are distinct.
Every contestant hopes that he can find a teammate so that their team’s strength is as high as possible. That is, a contestant will form a team with highest strength possible by choosing a teammate from ones who are willing to be a teammate with him/her. More formally, two people A and B may form a team if each of them is the best possible teammate (among the contestants that remain unpaired) for the other one.
Can you determine who will be each person’s teammate?
There are 2n lines in the input.
The first line contains an integer n (1 ≤ n ≤ 400) — the number of teams to be formed.
The i-th line (i > 1) contains i - 1 numbers ai1, ai2, ... , ai(i - 1). Here aij (1 ≤ aij ≤ 106, all aij are distinct) denotes the strength of a team consisting of person i and person j (people are numbered starting from 1.)
Output a line containing 2n numbers. The i-th number should represent the number of teammate of i-th person.
2
6
1 2
3 4 5
2 1 4 3
3
487060
3831 161856
845957 794650 976977
83847 50566 691206 498447
698377 156232 59015 382455 626960
6 5 4 3 2 1
In the first sample, contestant 1 and 2 will be teammates and so do contestant 3 and 4, so the teammate of contestant 1, 2, 3, 4 will be 2, 1, 4, 3 respectively.
题目大意：给一个下三角矩阵，要求选2n组人，每组两人，aij表示i和j在一起的分数，每次选的结果都是当前可能的最大值，一个人只能在一组里
题目分析：考虑aij只有1e6，果断暴力搞，用vector存坐标，然后从最大值往1枚举判断即可，已经成组的标记一下
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int const MAX = 1e6 + 5;
int ans[MAX];
vector <int> vt[MAX];int main()
{int n, tmp, ma = 0;scanf("%d", &n);n <<= 1;for(int i = 2; i <= n; i++){for(int j = 1; j < i; j++){scanf("%d", &tmp);vt[tmp].push_back(i);vt[tmp].push_back(j);ma = max(ma, tmp);}}for(int i = ma; i >= 1; i--){int sz = vt[i].size();if(sz > 0){int x = vt[i][0], y = vt[i][1];if(ans[x] == 0 && ans[y] == 0){ans[x] = y;ans[y] = x;}}}for(int i = 1; i < n; i++)printf("%d ", ans[i]);printf("%d\n", ans[n]);
}
There is a polyline going through points (0, 0) – (x, x) – (2x, 0) – (3x, x) – (4x, 0) – ... - (2kx, 0) – (2kx + x, x) – ....
We know that the polyline passes through the point (a, b). Find minimum positive value x such that it is true or determine that there is no such x.
Only one line containing two positive integers a and b (1 ≤ a, b ≤ 109).
Output the only line containing the answer. Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 9. If there is no such x then output - 1 as the answer.
3 1
1.000000000000
1 3
-1
4 1
1.250000000000
You can see following graphs for sample 1 and sample 3.
题目大意：求最小的x使得，点(a,b)在这个锯齿图形上
题目分析：首先由于斜率为正负1，可以得到点(a,b)两边在x轴上的点坐标为(a-b,0)和(a+b,0)，一个周期T=2b，所以，通过(a-b)/2b和(a+b)/2b可以得到以(a,b)为顶点的图形的周期范围，很难说清楚，画个图一下子就能看出来，显然以(a+b)/2b的更优，因为将它的x提高，它的边界线可以更快的经过(a,b)点，这里必须画图，说不清楚，所以答案就是(a+b)/2T了，注意a<b显然不可能
#include <cstdio>int main()
{int a, b;scanf("%d %d", &a, &b);if(a < b){printf("-1\n");return 0;}int T = (a + b) / 2 / b;double ans = (double) (a + b) / (double) T / 2.0;printf("%.10f\n", ans);
}
You are given n numbers a1, a2, ..., an. You can perform at most k operations. For each operation you can multiply one of the numbers by x. We want to make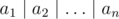 
as large as possible, where 
denotes the bitwise OR.
Find the maximum possible value of 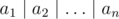after performing at most k operations optimally.
The first line contains three integers n, k and x (1 ≤ n ≤ 200 000, 1 ≤ k ≤ 10, 2 ≤ x ≤ 8).
The second line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 109).
Output the maximum value of a bitwise OR of sequence elements after performing operations.
3 1 2 1 1 1
3
4 2 3 1 2 4 8
79
For the first sample, any possible choice of doing one operation will result the same three numbers 1, 1, 2 so the result is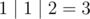 
.
For the second sample if we multiply 8 by 3 two times we'll get 72. In this case the numbers will become 1, 2, 4, 72 so the OR value will be 79 and is the largest possible result.
题目大意：n个数字，可以对任意一个数字乘x，最多乘k次，现在求乘完后的序列的或和最大是多少
题目分析：首先确定k次必须全都乘到一个数字上，因为每乘1次二进制最高位至少左移一位，这样或出来的结果肯定是最大的，但是注意不是乘当前最大的那个数，比如1010和1001，分别成2得10100和10010，假设我要或的数是10100那显然后面的更大，因此要枚举每个数，还要预处理前缀／后缀或和，然后O(n)枚举乘的那个数字取最大即可
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
int const MAX = 2e5 + 5;
ll l[MAX], r[MAX], a[MAX];int main()
{int n, k, x;scanf("%d %d %d", &n, &k, &x);for(int i = 1; i <= n; i++)scanf("%I64d", &a[i]);for(int i = 1; i <= n; i++)l[i] = l[i - 1] | a[i];for(int i = n; i >= 1; i--)r[i] = r[i + 1] | a[i];ll tmp = 1;for(int i = 0; i < k; i++)tmp *= x;ll ans = 0;for(int i = 1; i <= n; i++)ans = max(ans, l[i - 1] | (a[i] * tmp) | r[i + 1]);printf("%I64d\n", ans);
}
You are given a sequence of n integers a1, a2, ..., an.
Determine a real number x such that the weakness of the sequence a1 - x, a2 - x, ..., an - x is as small as possible.
The weakness of a sequence is defined as the maximum value of the poorness over all segments (contiguous subsequences) of a sequence.
The poorness of a segment is defined as the absolute value of sum of the elements of segment.
The first line contains one integer n (1 ≤ n ≤ 200 000), the length of a sequence.
The second line contains n integers a1, a2, ..., an (|ai| ≤ 10 000).
Output a real number denoting the minimum possible weakness of a1 - x, a2 - x, ..., an - x. Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 6.
3 1 2 3
1.000000000000000
4 1 2 3 4
2.000000000000000
10 1 10 2 9 3 8 4 7 5 6
4.500000000000000
For the first case, the optimal value of x is 2 so the sequence becomes - 1, 0, 1 and the max poorness occurs at the segment "-1" or segment "1". The poorness value (answer) equals to 1 in this case.
For the second sample the optimal value of x is 2.5 so the sequence becomes - 1.5, - 0.5, 0.5, 1.5 and the max poorness occurs on segment "-1.5 -0.5" or "0.5 1.5". The poorness value (answer) equals to 2 in this case.
题目大意：n个数字，每个数字可以加上一个实数x，现在要使得操作完后的数列的连续和的最大值最小，求x
题目分析：最大最小显然二分，可是二分什么？可以发现对于原数列的连续和最大要么是正连续和最大，要么是连续负数的绝对值最大，显然如果是最大正连续和大于最大负连续和的绝对值，说明x偏小，可以增大x的值，使得正值变小，负值的绝对值变大，二分边界显然是－10000到10000，注意这里的精度很奇妙，1e-10 wa了，1e-15 T了， 1e-12 AC
#include <cstdio>
int const MAX = 2e5 + 5;
double const EPS = 1e-12;
int a[MAX];int main()
{int n;scanf("%d", &n);for(int i = 1; i <= n; i++)scanf("%d", &a[i]);double l = -10000, r = 10000;double cur1, ma, cur2, mi, mid;while(r - l > EPS){cur1 = cur2 = ma = mi = 0;mid = (l + r) / 2;for(int i = 1; i <= n; i++){cur1 += a[i] - mid;if(cur1 < 0)cur1 = 0;if(cur1 > ma)ma = cur1;cur2 += a[i] - mid;if(cur2 > 0)cur2 = 0;if(cur2 < mi)mi = cur2;}if(ma > -mi)l = mid;elser = mid;}printf("%.10f\n", ma);
}这篇关于Codeforces Round #320 (Div. 2) [Bayan Thanks-Round] (ABCDE题解)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
