[Offer收割]编程练习赛1 hihocoder 1268 九宫 (DFS)

描述

小Hi最近在教邻居家的小朋友小学奥数，而最近正好讲述到了三阶幻方这个部分，三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中，使得每一行、每一列和每一条对角线的和都是相同的。

三阶幻方又被称作九宫格，在小学奥数里有一句非常有名的口诀：“二四为肩，六八为足，左三右七，戴九履一，五居其中”，通过这样的一句口诀就能够非常完美的构造出一个九宫格来。

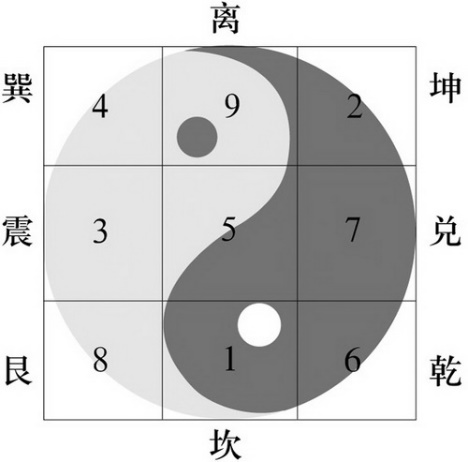
有意思的是，所有的三阶幻方，都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小Hi准备将一个三阶幻方（不一定是上图中的那个）中的一些数组抹掉，交给邻居家的小朋友来进行还原，并且希望她能够判断出究竟是不是只有一组解。

而你呢，也被小Hi交付了同样的任务，但是不同的是，你需要写一个程序~

输入

输入仅包含单组测试数据。

每组测试数据为一个3*3的矩阵，其中为0的部分表示被小Hi抹去的部分。

对于100%的数据，满足给出的矩阵至少能还原出一组可行的三阶幻方。

输出

如果仅能还原出一组可行的三阶幻方，则将其输出，否则输出“Too Many”（不包含引号）。

样例输入

0 7 2
0 5 0
0 3 0

样例输出

6 7 2
1 5 9
8 3 4

题目链接：http://hihocoder.com/problemset/problem/1268

题目分析：裸DFS

#include <cstdio>
#include <cstring>
int x[5][5], ans[5][5];
bool has[10];
int cnt, tmp;
bool flag;bool ok()
{int sum = x[1][1] + x[1][2] + x[1][3];if(x[2][1] + x[2][2] + x[2][3] != sum)return false;if(x[3][1] + x[3][2] + x[3][3] != sum)return false;if(x[1][1] + x[2][1] + x[3][1] != sum)return false;if(x[1][2] + x[2][2] + x[3][2] != sum)return false;if(x[1][3] + x[2][3] + x[3][3] != sum)return false;if(x[1][1] + x[2][2] + x[3][3] != sum)return false;if(x[1][3] + x[2][2] + x[3][1] != sum)return false;return true;
}void DFS(int i, int j)
{if(i == 4 && ok()){cnt ++;if(cnt == 1)memcpy(ans, x, sizeof(x));return;}if(x[i][j]){if(j == 3)DFS(i + 1, 1);elseDFS(i, j + 1);}else{for(int num = 1; num <= 9; num++){if(!has[num]){has[num] = true;x[i][j] = num;if(j == 3)DFS(i + 1, 1);elseDFS(i, j + 1);has[num] = false;x[i][j] = 0;}}}
}int main()
{cnt = 0;flag = false;for(int i = 1; i <= 3; i++){for(int j = 1; j <= 3; j++){scanf("%d", &x[i][j]);has[x[i][j]] = true;}}DFS(1, 1);if(cnt == 1)for(int i = 1; i <= 3; i++)for(int j = 1; j <= 3; j++)printf("%d%c", ans[i][j], j == 3 ? '\n' : ' ');elseprintf("Too Many\n");
}