本文主要是介绍GAMES101 学习3,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Lecture 13 ~ 16
Shadow mapping
- 一种图像空间算法
- 生成阴影时不需要知道场景中的几何信息
- 会产生走样现象
最重要的思想:如果有的点不在阴影里你又能看到这个点,那么说明摄像机可以看到这个点,光源也可以看到这个点
经典的Shadow mapping 只能处理电光源
步骤:
- 从光源看像场景,记录看到的任何点的深度
- Project visible points in eye view back to light source 眼睛看向场景,将看到的场景投影回光源,查看记录的深度是否一致。如果只被光线看到,不被相机看到,就不会被渲染;如果被相机看到,没被光线看到,就是阴影。
问题:画面会脏,数值精度问题(浮点数的相等不好判断,可以改判大小,或加个bias,但效果不好);受限于shadow mapping的分辨率;只能产生硬阴影。
应用:所有的3d游戏和早期动画

光栅化的问题
光栅化的渲染是将场景的渲染任务按层次拆解:物体——三角面——像素。这种拆解会导致全局信息的丢失,因此光栅化实现不了软阴影、间接光照等。
shadow mapping
光栅化没法考虑全局光照(GI),只能计算直接光照,没法考虑光源与物体间的遮挡,无法计算阴影。那怎么产生阴影的效果?用shadow mapping!但是只能处理点/方向光源,只能产生硬阴影(要么在阴影里,要么不在)。光栅化是快速的,近似的效果


Ray Casting 光线投射(by Author Appel)
光线追踪 --> 实时,很慢,经常用来进行离线的制作,比如用来制作电影
Light Rays (假设)
- 光线沿着直线传播 (本身是错误的)
- 光线不会互相碰撞 (也是错误的)
- 光线是从光源发射出来然后经过反射最终到达人眼 (利用了光线的可逆性)
假设:
- 人的眼睛是针孔摄像机,光源是点光源
- 光线打到场景物体上会发生完美的反射/折射
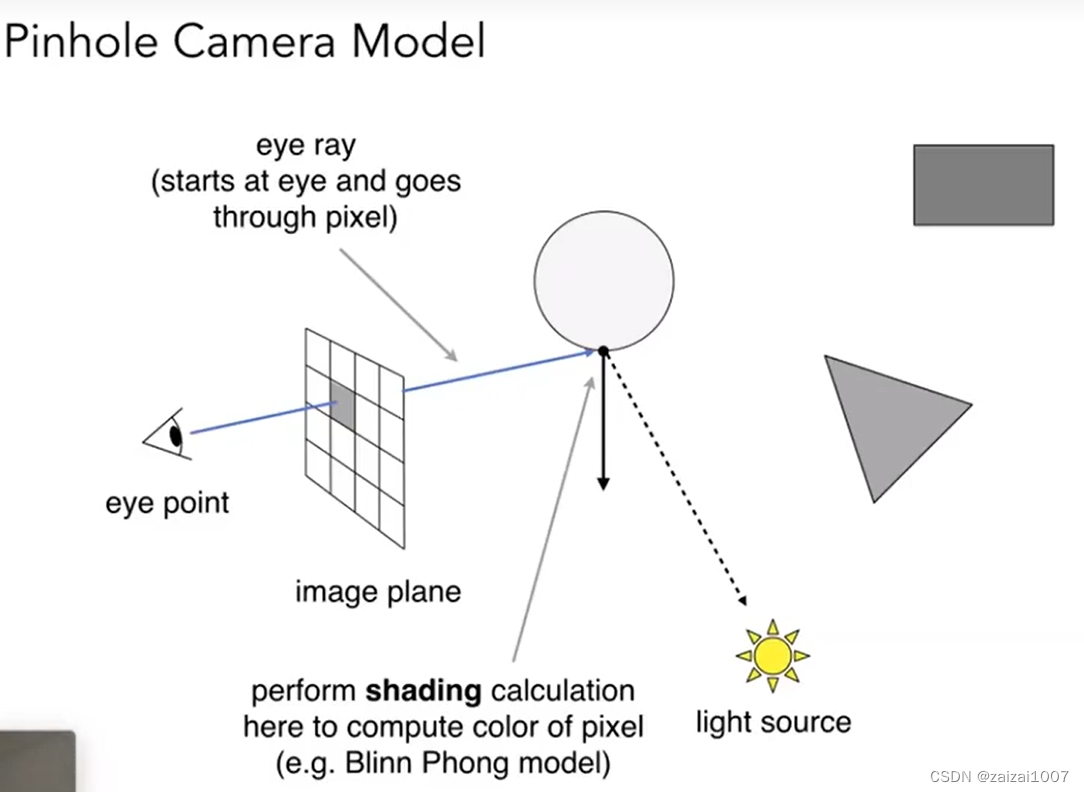
Eye Ray :从眼睛开始,往成像屏幕的任何一个像素投射,打到场景中某个位置(最近的交点,因为人眼肯定是看到最近的东西,从而也解决了深度测试的问题)
Shadow Ray :再从这个交点往光源连一条线,如果这条线上没有任何东西阻挡,那我们就认为该点被光线照亮,如果有,就认为该点在阴影中
从相机出发,对于每个像素点向场景投射光线,直到光线与场景中第一个物体相交,在交点处,根据物体本身性质、光源属性和光照模型等来计算像素点的颜色;
光线投射只考虑投射光线,光线与物体相交后不会继续跟踪,不考虑后续的折射、反射等。
whitted-style 光线追踪 递归

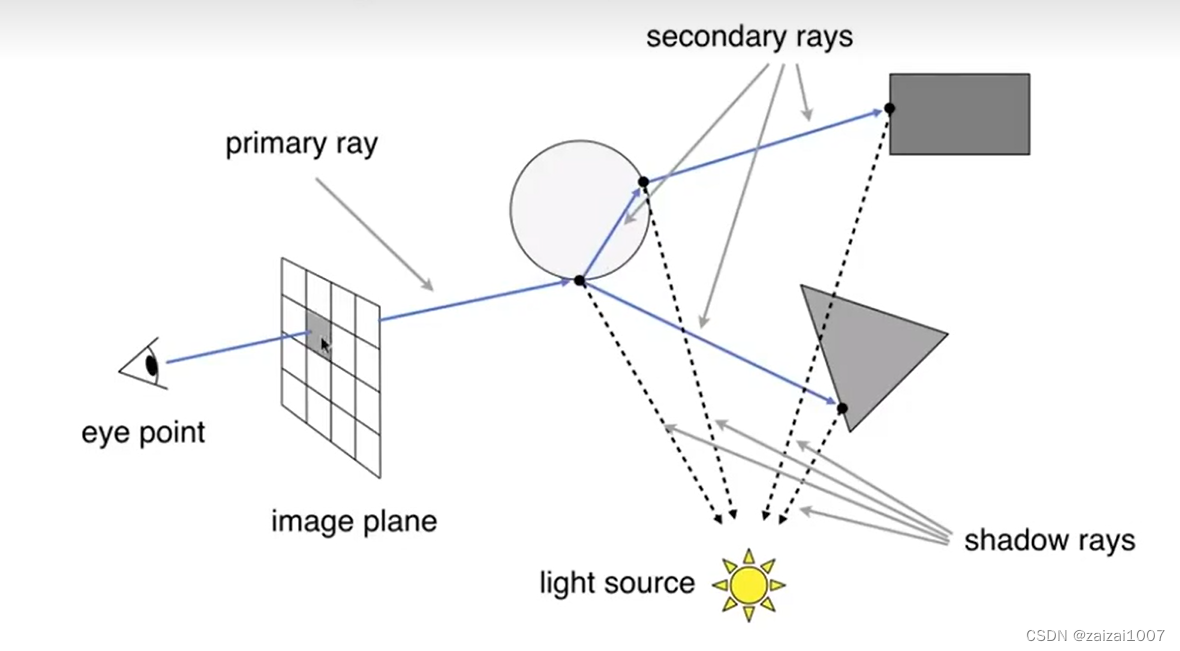
Whitted 主要说在任何一个点,光线可以继续传播
- 计算折射,反射
- 每一个和场景相交的点都与光源做连线,进行着色
技术问题
Ray - Surface Intersection 求光线与表面的交点
数学上的光线有一个起点,有方向,就是一条射线

光线与物体求交
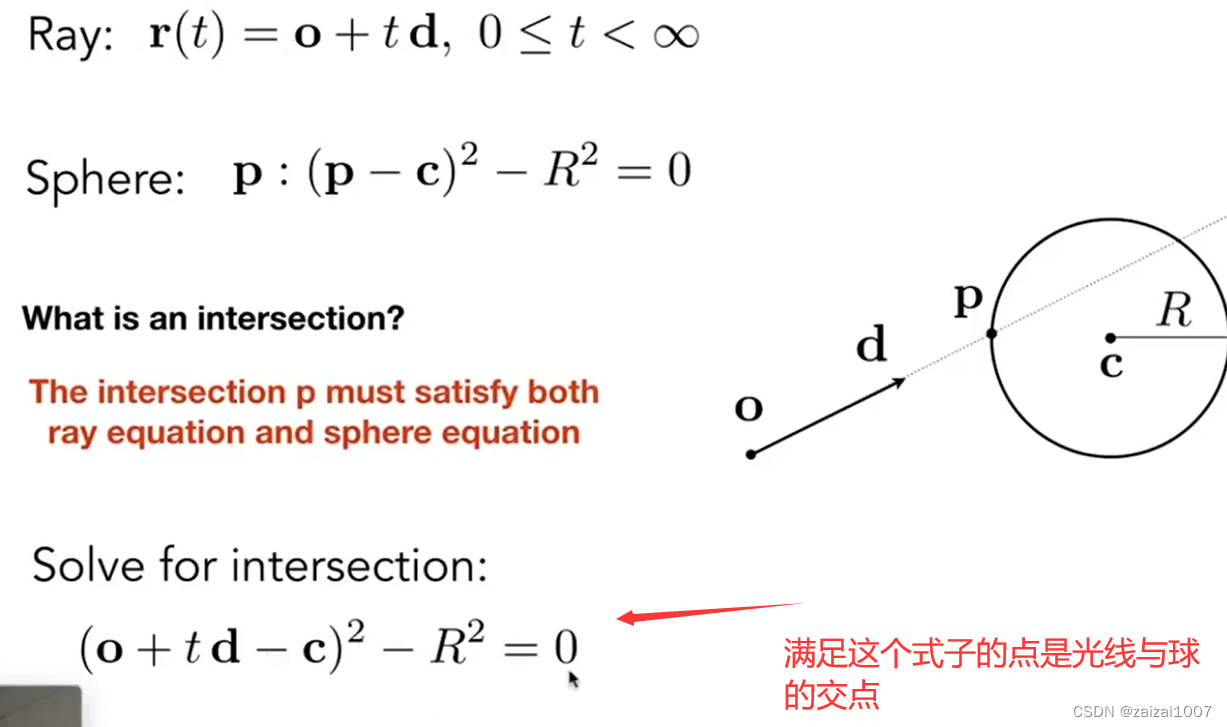

推广到隐式表面

得到的根必须具有实际意义
- 必须是正的
- 必须是实数,不能是虚数
那么对于显式的表面呢?
可以判断是否在物体内:一个点在封闭的图形内,往任意方向打一束光线储出去
- 奇数个交点 -- 物体内
- 偶数个交点 -- 物体外
光线和三角形求交 -- 太慢了 做法分解:
- 求光线与平面的交点
- 判断交点是否在三角形内部
定义一个平面:一条法线,一个点
法线与平面上任意一条线段垂直
定义点 p 的要求:任何一个在平面上的点 p 与给定 p`的连线都与 N 法线垂直


重心坐标求解

左边式子:光线方程 右边式子:用中心坐标表示的三角形内的任意一点
求解:t ,b1,b2 三个未知量,三个式子 -- 克莱姆法则
要求:t 是正数,1 - b1 - b2 非负, b1 ,b2 非负
光线与表面求交的加速算法
不可能光线与每个三角形求一次交,加速的重要概念 -- 包围盒 (Bounding Volumes )
参考文章:GAMES101 梳理 / 个人向图形学笔记-CSDN博客
13_Ray Tracing_Whitted Style Ray Tracing (yuque.com)
这篇关于GAMES101 学习3的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








