本文主要是介绍Codeforces Round 933(Div.3) A~F,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A.Rudolf and the Ticket(暴力)
题意:
鲁道夫要去拜访伯纳德,他决定乘坐地铁去找他。车票可以在接受两个硬币的机器上购买,这两个硬币的总和不超过 k k k。
鲁道夫有两个装硬币的口袋。左边口袋里有 n n n枚面值为 b 1 , b 2 , … , b n b_1,b_2,\dots,b_n b1,b2,…,bn 的硬币。右边口袋里有 m m m枚面值为 c 1 , c 2 , … , c m c_1,c_2,\dots,c_m c1,c2,…,cm 的硬币。他想从左边口袋和右边口袋各取出一枚硬币(共两枚)。
请帮助鲁道夫判断有多少种方法可以选择序号 f f f和 s s s,从而使 b f + c s ≤ k b_f+c_s\le k bf+cs≤k。
分析:
数据量较小,暴力枚举所有方案然后判断是否合法即可。
代码:
#include<bits/stdc++.h>using namespace std;int main() {int t;cin >> t;while (t--) {int n, m, k;cin >> n >> m >> k;vector<int> b(n), c(m);for (int i = 0; i < n; ++i)cin >> b[i];for (int i = 0; i < m; ++i)cin >> c[i];int ans = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (b[i] + c[j] <= k)ans++;}}cout << ans << endl;}return 0;
}
B.Rudolf and 121(贪心)
题意:
Rudolf有一个由 n n n个整数组成的数组 a a a,元素的编号从 1 1 1到 n n n。
在一次操作中,他可以选择序号 i i i( 2 ≤ i ≤ n − 1 2\le i\le n-1 2≤i≤n−1)并赋值:
- a i − 1 = a i − 1 − 1 a_{i-1}=a_{i-1}-1 ai−1=ai−1−1
- a i = a i − 2 a_i=a_i-2 ai=ai−2
- a i + 1 = a i + 1 − 1 a_{i+1}=a_{i+1}-1 ai+1=ai+1−1
鲁道夫可以任意多次使用这个运算。任何索引 i i i都可以使用 0 0 0次或更多次。
他能用这个运算使数组中的所有元素都等于零吗?
分析:
从前往后操作使 a i − 1 = 0 a_{i-1}=0 ai−1=0,若 a i a_i ai小于 0 0 0则不行。
代码:
#include<bits/stdc++.h>using namespace std;void solve() {int n;cin >> n;int a[n + 1];for (int i = 1; i <= n; i++) {cin >> a[i];}for (int i = 2; i < n; i++) {int t = a[i - 1];if (t < 0) {cout << "NO" << endl;return;}a[i] -= 2 * t;a[i + 1] -= t;}if (a[n - 1] == 0 && a[n] == 0) {cout << "YES" << endl;} else {cout << "NO" << endl;}
}int main() {int t;cin >> t;while (t--) {solve();}return 0;
}
C.Rudolf and the Ugly String(贪心)
题意:
鲁道夫有一个长度为 n n n的字符串 s s s。如果字符串 s s s包含子串 † ^\dagger †"pie"或子串"map",鲁道夫就会认为这个字符串 s s s很丑,否则字符串 s s s将被视为优美字符串。
例如,“ppiee”、“mmap”、“dfpiefghmap"是丑字符串,而"mathp”、"ppiiee"是优美字符串。
鲁道夫希望通过删除一些字符来缩短字符串 s s s使其美观。
主角不喜欢吃力,所以他要求你删除最少的字符,使字符串变得漂亮。他可以删除字符串中任何位置的字符(不仅仅是字符串的开头或结尾)。
† ^\dagger † 如果字符串 b b b中存在等于 a a a的连续字符段,则字符串 a a a是 b b b的子串。
分析:
发现"pie"和"map"都含有"p",因此可以遇到两者就删除"p"。
代码:
#include<bits/stdc++.h>using namespace std;int main() {int t;cin >> t;while (t--) {int n;cin >> n;string s;cin >> s;int ans = 0;vector<int> mp(n + 1, 0);string t1 = "map";string t2 = "pie";for (int i = 0; i < n - 2; i++) {if (mp[i] == 1) {continue;}if (s.substr(i, 3) == t1) {ans++;mp[i + 2] = 1;} else if (s.substr(i, 3) == t2) {ans++;mp[i] = 1;}}cout << ans << endl;}return 0;
}
D.Rudolf and the Ball Game(模拟)
题意:
鲁道夫和伯纳德决定和朋友们玩一个游戏。 n n n人站成一圈,开始互相扔球。他们按顺时针顺序从 1 1 1到 n n n依次编号。
我们把球从一个人向他的邻居移动称为一次过渡。移动可以顺时针或逆时针进行。
我们把从玩家 y 1 y_1 y1到玩家 y 2 y_2 y2的顺时针(逆时针)距离称为从玩家 y 1 y_1 y1到玩家 y 2 y_2 y2所需的顺时针(逆时针)转换次数。例如,如果 n = 7 n=7 n=7,那么从 2 2 2到 5 5 5的顺时针距离是 3 3 3,而从 2 2 2到 5 5 5的逆时针距离是 4 4 4。
最初,球在编号为 x x x的玩家的手中(玩家按顺时针方向编号)。在第 i i i次移动中,持球者将其投掷到 r i r_i ri距离处( 1 ≤ r i ≤ n − 1 1≤r_i≤n−1 1≤ri≤n−1),方向可以是顺时针或逆时针。例如,如果有 7 7 7名玩家,并且第 2 2 2名玩家接到球后将其投出 5 5 5个距离,则球将被第 7 7 7名玩家(顺时针投掷),或者第 4 4 4名玩家抓住(逆时针投掷)。下面显示了此示例的插图。
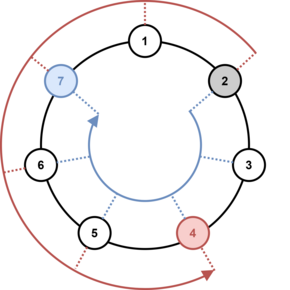
由于下雨,比赛在 m m m次投掷后中断。雨停后,大家又聚在一起继续比赛。但是,没有人记得球在谁手里。但是,伯纳德记住了每次投掷的距离和一些投掷的方向(顺时针或逆时针)。
鲁道夫请您帮助他,根据伯纳德提供的信息,计算出 m m m次抛球后可能拿到球的队员人数。
分析:
用 s e t set set维护下当前可能在的地方,模拟即可。
代码:
#include<bits/stdc++.h>using namespace std;void solve() {int n, m, x;cin >> n >> m >> x;set<int> se;se.insert(x);set<int> t;for (int i = 0; i < m; ++i) {int d;char c;cin >> d >> c;for (auto v: se) {if (c == '0') {int y = (v + d) % n;if (y == 0)y = n;t.insert(y);} else if (c == '1') {int y = (v - d + n) % n;if (y == 0)y = n;t.insert(y);} else {int y = (v + d) % n;if (y == 0)y = n;t.insert(y);y = (v - d + n) % n;if (y == 0)y = n;t.insert(y);}}se = t;t.clear();}cout << se.size() << endl;for (auto v: se)cout << v << " ";cout << endl;
}int main() {int t;cin >> t;while (t--) {solve();}return 0;
}
E.Rudolf and k Bridges(动态规划)
题意:
伯纳德喜欢拜访鲁道夫,但他总是迟到。问题是伯纳德必须乘渡船过河。鲁道夫决定帮助他的朋友解决这个问题。
这条河是由 n n n行和 m m m列组成的网格。第 i i i行和第 j j j列的交点数字 a i , j a_{i,j} ai,j表示相应单元格的深度。第一列和最后一列的所有单元格都对应河岸,因此它们的深度为 0 0 0。

河流可能是这样的。
鲁道夫可以选择 ( i , 1 ) , ( i , 2 ) , … , ( i , m ) (i,1),(i,2),\ldots,(i,m) (i,1),(i,2),…,(i,m)行,并在其上架桥。在该行的每个单元格中,他都可以为桥安装一个桥墩。在第 ( i , j ) (i,j) (i,j)格安装桥墩的成本为 a i , j + 1 a_{i,j}+1 ai,j+1。安装桥墩必须满足以下条件:
- 必须在单元格 ( i , 1 ) (i,1) (i,1)中安装一个桥墩;
- 单元格 ( i , m ) (i,m) (i,m)中必须安装一个桥墩;
- 任何一对相邻桥墩之间的距离不得大于 d d d。桥墩 ( i , j 1 ) (i,j_1) (i,j1)和 ( i , j 2 ) (i,j_2) (i,j2)之间的距离为 ∣ j 1 − j 2 ∣ − 1 |j_1-j_2|-1 ∣j1−j2∣−1。
只建一座桥是很无聊的。因此,鲁道夫决定在河道的连续几行上建造 k k k座桥,即选择一些 i i i( 1 ≤ i ≤ n − k + 1 1\le i\le n-k+1 1≤i≤n−k+1),独立建造 k k k座桥。( 1 ≤ i ≤ n − k + 1 1\le i\le n-k+1 1≤i≤n−k+1),并在每一行 i , i + 1 , … , i + k − 1 i,i+1,\ldots,i+k-1 i,i+1,…,i+k−1上独立建造一座桥。请帮助鲁道夫尽量减少安装桥墩的总成本。
分析:
计算在第 i i i行造桥的最小代价,考虑 d p dp dp,状态转移方程为 d p j = d p k + a i , j + 1 dp_j=dp_{k}+a_{i,j}+1 dpj=dpk+ai,j+1, k k k为 [ j − k − 1 , j − 1 ] [j-k-1,j-1] [j−k−1,j−1],枚举 k k k的话会超时,需要维护单调队列来直接得到 k k k的值,通过 d p dp dp求出每行的最小代价。最后选择连续的 k k k行桥,使用前缀和维护然后枚举。
代码:
#include<bits/stdc++.h>typedef long long LL;
using namespace std;void solve() {int n, m, k, d;cin >> n >> m >> k >> d;LL a[n + 1][m + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> a[i][j];}}vector<LL> ans;for (int i = 1; i <= n; i++) {vector<LL> dp(m + 1, 0);deque<int> Q;while (!Q.empty()) {Q.pop_back();}dp[1] = a[i][1] + 1;Q.push_back(1);for (int j = 2; j <= m; j++) {if (!Q.empty() && j - Q.front() > d + 1)Q.pop_front();dp[j] = dp[Q.front()] + a[i][j] + 1;while (!Q.empty() && dp[Q.back()] > dp[j])Q.pop_back();Q.push_back(j);}ans.push_back(dp[m]);}LL pre[n + 1];pre[0] = ans[0];for (int i = 1; i < n; i++) {pre[i] = pre[i - 1] + ans[i];}LL cnt = pre[k - 1];for (int i = k; i < n; i++) {cnt = min(cnt, pre[i] - pre[i - k]);}cout << cnt << endl;
}int main() {int t;cin >> t;while (t--) {solve();}return 0;
}
F.Rudolf and Imbalance(数学)
题意:
鲁道夫准备了一组复杂度为 a 1 < a 2 < a 3 < ⋯ < a n a_1\lt a_2\lt a_3\lt\dots\lt a_n a1<a2<a3<⋯<an的 n n n个问题。他对平衡并不完全满意,因此他想最多增加一个问题来解决它。
为此,鲁道夫提出了 m m m个问题模型和 k k k个函数。第 i i i个模型的复杂度是 d i d_i di,第 j j j个函数的复杂度是 f j f_j fj。要创建一个问题,他需要选择值 i i i和 j j j( 1 ≤ i ≤ m 1\le i\le m 1≤i≤m, 1 ≤ j ≤ k 1\le j\le k 1≤j≤k, i i i)。( 1 ≤ i ≤ m 1\le i\le m 1≤i≤m, 1 ≤ j ≤ k 1\le j\le k 1≤j≤k),并将第 i i i个模型与第 j j j个函数相结合,得到一个复杂度为 d i + f j d_i+f_j di+fj的新问题(在数组 a a a中插入了一个新元素)。
为了确定集合的不平衡性,鲁道夫将问题的复杂度按升序排序,并找出 a i − a i − 1 a_i-a_{i-1} ai−ai−1的最大值( i > 1 i\gt 1 i>1)。
鲁道夫根据所描述的规则最多添加一个问题所能达到的最小不平衡值是多少?
分析:
由于最多插入一个,若 a a a存在多个最大差值,答案即为最大差值。
若只存在一个最大差值 r − l r-l r−l,即在 ( l , r ) (l,r) (l,r)之间插入,插入后的差值与原第二大差值比较即可。
考虑插入的数应该趋近于中间,为 m i d = l + r > > 1 mid=l+r>>1 mid=l+r>>1
而后枚举 d d d, f f f应该趋近于 m i d − d mid-d mid−d,二分出趋近于 m i d − d mid-d mid−d的 f f f,将求出的数与 l l l和 r r r取差值,维护最小差值即可。
代码:
#include<bits/stdc++.h>typedef long long LL;
using namespace std;void solve() {int n, m, k;cin >> n >> m >> k;vector<LL> a(n + 1), d(m + 1), f(k + 1);for (int i = 1; i <= n; i++) {cin >> a[i];}for (int i = 1; i <= m; i++) {cin >> d[i];}for (int i = 1; i <= k; i++) {cin >> f[i];}sort(a.begin() + 1, a.end());sort(d.begin() + 1, d.end());sort(f.begin() + 1, f.end());LL dist = -1;LL sd = -1;int cnt = 0;LL l = 0;LL r = 0;for (int i = 2; i <= n; i++) {LL t = a[i] - a[i - 1];if (t > dist) {if (dist != -1) {sd = dist;}dist = t;cnt = 1;l = a[i - 1];r = a[i];} else if (t == dist) {cnt++;sd = dist;} else if (sd < t) {sd = t;}}if (cnt > 1) {cout << dist << endl;return;}LL ans = dist;LL mid = (l + r + 1) / 2;for (int i = 1; i <= m; i++) {LL x = mid - d[i];auto it = lower_bound(f.begin() + 1, f.end(), x);if (it != f.end()) {x = *it;LL t = d[i] + x;if (t >= l && t <= r) {ans = min(ans, max(r - t, t - l));if (sd != -1) {ans = max(ans, sd);}}}if (it != f.begin() + 1) {it--;x = *it;LL t = d[i] + x;if (t >= l && t <= r) {ans = min(ans, max(r - t, t - l));if (sd != -1) {ans = max(ans, sd);}}}}cout << ans << endl;
}int main() {int t;cin >> t;while (t--) {solve();}return 0;
}
赛后交流
在比赛结束后,会在交流群中给出比赛题解,同学们可以在赛后查看题解进行补题。
群号: 704572101,赛后大家可以一起交流做题思路,分享做题技巧,欢迎大家的加入。
这篇关于Codeforces Round 933(Div.3) A~F的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



