本文主要是介绍遗传算法(Genetic Algorithm, GA)详解及其Python代码实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
前言:
一、遗传算法(Genetic Algorithm, GA)简介
二、遗传算法基本概念
二(1)目标函数——环境
二(2)一组解,最优解——种群,最适宜种群
二(3)解,编码——个体,基因型
二(4)解码——表现型 (难点)
二(5)交叉,变异——繁衍:染色体的交叉换组,基因突变
二(6)适应度——个体能力(难点)
二(7)选择——优胜劣汰
三、遗传算法过程
四、代码实现
四(1)所用库
四(2)初始变量定义
四(3)适应度函数、编码、解码、交叉、变异
四(4)建模,杂项,主函数
五、结果
前言:
本文是初学者(就是我!)在学习遗传算法当天做出的总结,希望以个人对于遗传算法学习过程,即从概念理解到代码实现、以二元函数为例,对其他初学者有一定的帮助。同时,也欢迎和期待各位大佬的批评和指正。
一、遗传算法(Genetic Algorithm, GA)简介
达尔文在他的著作《物种起源》中阐明了两个主要观点:1.物种是可变的,生物是进化的。2.自然选择是生物进化的动力。这些观点在遗传算法中依然适用,换言之,我们可通过对生物学“物竞天择,适者生存”的了解去理解消化遗传算法(高中生物还记得的话,遗传算法理解起来十分容易)。 言归正传,所谓遗传算法即是通过不断迭代来寻求最优解的一种过程,将次解淘汰,优解保留并重新进行迭代,在一次次计算中,不断地趋近(不是等于)最优解的算法。
二、遗传算法基本概念
想要理解遗传算法中的变量以及函数意义,我们不妨从生物学角度入手。即在给定区域内,带来一批各种性状可繁殖的同一物种,在多年的繁衍后优胜劣汰保留适应性状的一组个体。
二(1)目标函数——环境
在一定区域内(目标函数x,y值的取值范围)的环境水平,如地势高低(F(x,y)值的大小)

二(2)一组解,最优解——种群,最适宜种群
在给定区域内,存在于环境中不同位置的个体数目适中、可繁衍的一个种群(一组不断迭代寻求最优的解)在不断繁衍优胜劣汰后保留下来的的种群(在迭代结束后的一组解,其每个解应十分靠近最优解)注意:如图所示,初始组为随机分布在F(x,y)上的,另外,这组解不应太大(计算复杂)也不应太小(陷入局部最优解,如下图稍小的峰值)
一组解
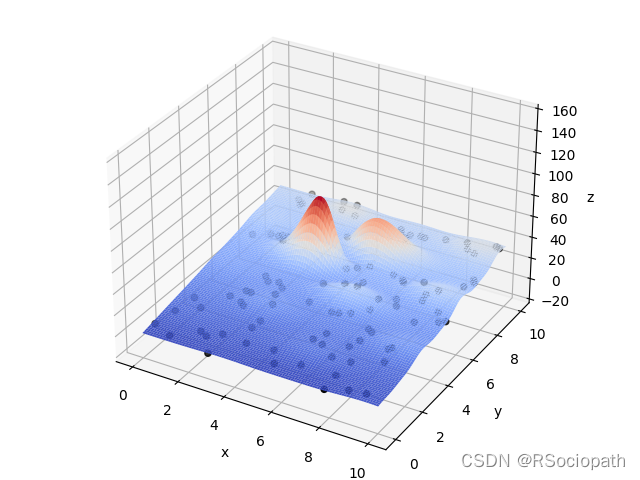
最优解

局部最优解
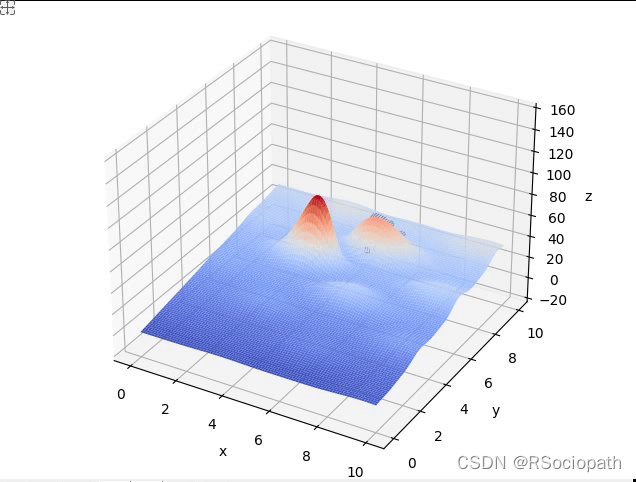
二(3)解,编码——个体,基因型
种群中的个体(一个解,即上图中的一个黑点)及其基因型(在遗传算法中通常以一个二进制编码储存)
二(4)解码——表现型 (难点)
根据基因型导致的表现型(将解的二进制数组转化为相应的x,y值)
在具体讲述解码过程之前我们需要引入四个概念:
二进制编码长度l
精度:将一条线段化为无数小线段,每条小线段的距离(之所以采用精度是因为我们无法取到线段上每一个点,只可以退而求次改为线段上的2^l个点。其所分割出的2^l-1个小线段的长度称为精度)
取值下界:x或y的最小值(二元函数为例)
取值上界:x或y的最大值
-
:给定的x或y的范围的长度
:将一个解二进制编码转换为十进制
x:解的x或y值
精度: 解码:
二(5)交叉,变异——繁衍:染色体的交叉换组,基因突变
在产生后代时,父辈染色体交叉,繁衍中可能出现基因突变,导致子辈基因型出现变化(根据已有解创造下一组解的一部分)注意:并非全部解都需要进行交叉或变异。在遗传算法中,并不是将解的二进制编码折半交叉,而是随机取一段不定长部分进行交换
交叉是为了确保大方向朝着最优解方向,变异是为了不产生局部最优解
蓝色部分进行交换,绿色部分出现变异
| A | ....... | 1 | 1 | 1 | 0 | 1 | 0 | 0 | ....... |
| B | ....... | 0 | 1 | 0 | 0 | 1 | 1 | 0 | ....... |
| A' | ....... | 1 | 1 | 0 | 0 | 1 | 0 | 1 | ....... |
| B' | ....... | 0 | 1 | 1 | 0 | 1 | 1 | 0 | ....... |
上图所示的为两点交叉以及位点变异,其余在本文中不加以赘述,可自行查找资料
二(6)适应度——个体能力(难点)
你没能力能活多久?(解的适应度函数值与一组解适应度函数值之和的比值表示在迭代中解被保留下来的概率)
在这里我们引入
适应度函数,其中
为一个解,注意:适应度函数值非负。
:这一组解中最小值
:这一组解中最大值
最大值问题:
最小值问题:
上述两个分段函数均表示概率所以非负,并且解的适应度函数值都是越大越容易保留(不一定保留)
二(7)选择——优胜劣汰
在产生新一代种群时,注定有父辈和子辈被淘汰(根据适应度有偏向的选出下一组同样大小的一组解)
三、遗传算法过程
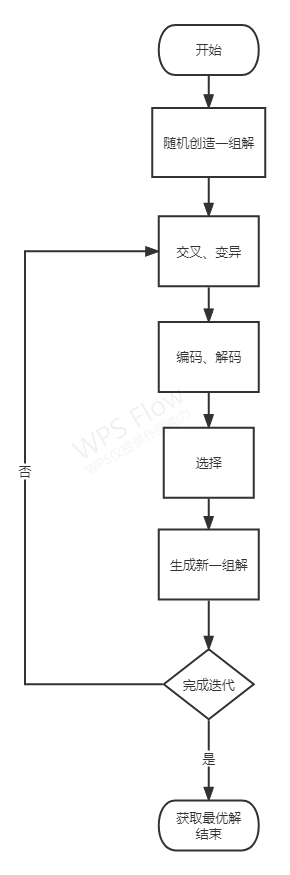
四、代码实现
四(1)所用库
安装库请看:库的安装
import numpy as np
from numpy.ma import cos
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D # 建模,不必需
import datetime # 统计时间,不必需四(2)初始变量定义
DNA_SIZE = 24 # 编码长度
POP_SIZE = 100 # 种群大小
CROSS_RATE = 0.5 # 交叉率
MUTA_RATE = 0.15 # 变异率
Iterations = 50 # 迭代次数
X_BOUND = [0, 10] # X区间
Y_BOUND = [0, 10] # Y区间def F(x, y): # 函数return (6.452*(x+0.125*y)*(cos(x)-cos(2*y))**2)/(0.8+(x-4.2)**2+2*(y-7)**2)+3.226*y其中函数为:
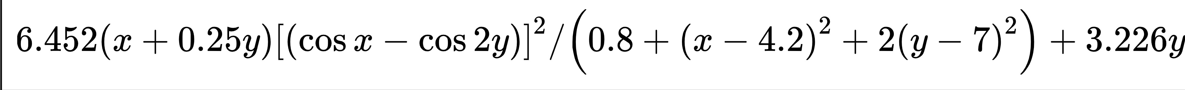
四(3)适应度函数、编码、解码、交叉、变异
def F(x, y): # 函数return (6.452*(x+0.125*y)*(cos(x)-cos(2*y))**2)/(0.8+(x-4.2)**2+2*(y-7)**2)+3.226*ydef getfitness(pop): # 适应度函数x, y = decodeDNA(pop)temp = F(x, y)return (temp-np.min(temp))+0.0001def decodeDNA(pop): # 二进制转坐标,解码x_pop = pop[:, 1::2]y_pop = pop[:, ::2]# .dot()用于矩阵相乘x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]return x, ydef select(pop, fitness): # 选择temp = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True, p=fitness/(fitness.sum()))return pop[temp]# mutation函数以及crossmuta函数均为编码过程def mutation(temp, MUTA_RATE): # 变异if np.random.rand() < MUTA_RATE:mutate_point = np.random.randint(0, DNA_SIZE)temp[mutate_point] = temp[mutate_point] ^ 1 # ^为异或运算def crossmuta(pop, CROSS_RATE): # 交叉new_pop = []for i in pop:temp = iif np.random.rand()<CROSS_RATE:j = pop[np.random.randint(POP_SIZE)]cpoints1 = np.random.randint(0, DNA_SIZE*2-1)cpoints2 = np.random.randint(cpoints1, DNA_SIZE*2)temp[cpoints1:cpoints2] = j[cpoints1:cpoints2]mutation(temp, MUTA_RATE)new_pop.append(temp)return new_pop其中有一些比较少见的函数如:
numpy. arange 详见Python – numpy.arange()
numpy.random.choice 详见numpy.random.choice()
以上函数需要大连篇幅讲解,请自行查阅详细资料。
四(4)建模,杂项,主函数
##更新于2023.10.8
目前出现了在社区版能跑通在企业版不能跑通的问题,以及社区版更新matplotlib包为版本3.4以上时报错的问题。具体修改代码如下注释。
def print_info(pop): # 输出最优解等fitness = getfitness(pop)maxfitness = np.argmax(fitness)print("max_fitness", fitness[maxfitness])x, y = decodeDNA(pop)print("最优的基因型:", pop[maxfitness])print("(x,y):", (x[maxfitness], y[maxfitness]))print("F(x,y)_max=", F(x[maxfitness], y[maxfitness]))def plot_3d(ax): # 建模X = np.linspace(*X_BOUND, 100)Y = np.linspace(*Y_BOUND, 100)X, Y = np.meshgrid(X, Y)Z = F(X, Y)ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)ax.set_zlim(-20,160)ax.set_xlabel('x')ax.set_ylabel('y')ax.set_zlabel('z')plt.pause(0.5)plt.show()if __name__=="__main__": # 主函数fig = plt.figure()ax = Axes3D(fig)#ax = Axes3D(fig, auto_add_to_figure=False)# fig.add_axes(ax)
#如果出现程序跑通但不显示图片问题请使用这两行代码,注释掉ax=Axes3D(fig)plt.ion()plot_3d(ax)pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2))start_t = datetime.datetime.now()for i in range(Iterations):print("i:", i)x, y = decodeDNA(pop)if 'sca' in locals():sca.remove()sca = ax.scatter(x, y, F(x, y), c="black", marker='o')plt.show()plt.pause(0.1)pop = np.array(crossmuta(pop, CROSS_RATE))fitness = getfitness(pop)pop = select(pop, fitness)end_t = datetime.datetime.now()print((end_t-start_t).seconds)print_info(pop)plt.ioff()plot_3d(ax)五、结果
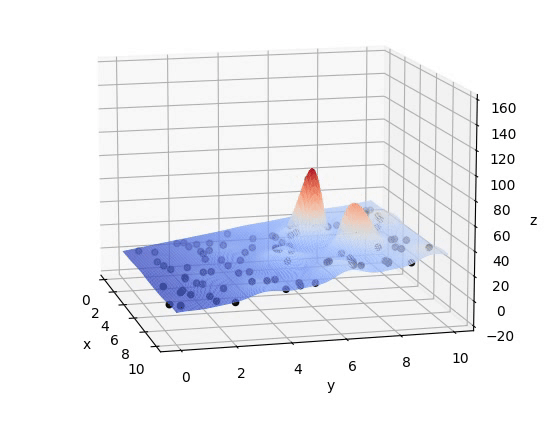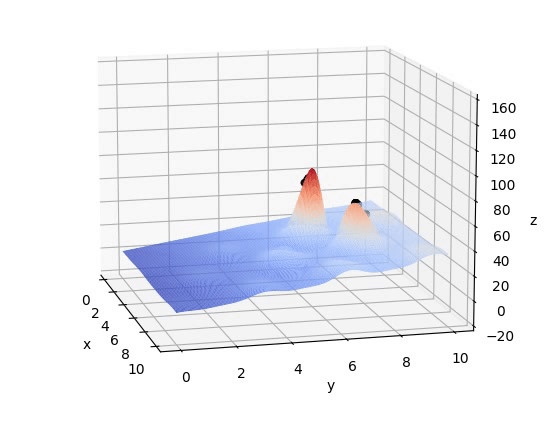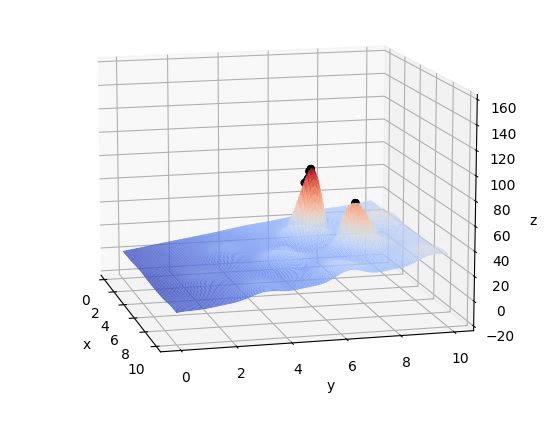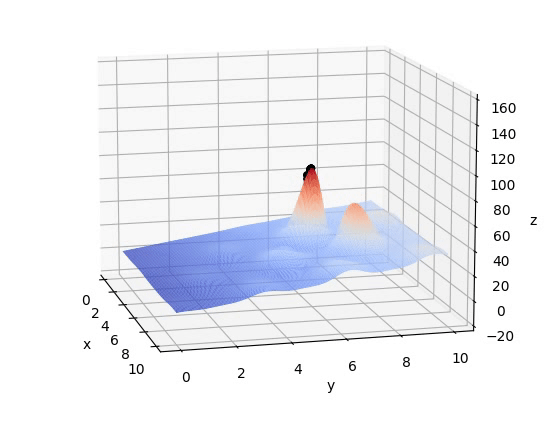
这篇关于遗传算法(Genetic Algorithm, GA)详解及其Python代码实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






