GNG论文+实验

GNG论文思路：

• GNG-A
• OGNG
• GNG-T
• GNG-Ada中的loss
• GNG降维可视化
• GWR

前言

更新：2024/01/11
上世纪 90 年代，人工神经网络研究人员得出了一个结论：有必要为那些缺少网络层固定拓扑特征的运算机制，开发一个新的类。也就是说，人工神经在特征空间内的数量和布置并不会事先指定，而是在学习此类模型的过程中、根据输入数据的特性来计算，独立调节也与其适应。我们注意到，CNN/RNN这种在训练开始前就预先设置好了网络的神经元拓朴结构而训练的过程只是在调整这些神经元的参数，对于无监督学习的场景来说，大多数情况下，我们是无法预先知道输入数据空间的拓朴分布的。

理解上就是GNG是一种动态增长型神经网络，举个例子，对于神经网络中有的任务需要选择小的网络结构，有的需要使用大的网络结构，GNG相当于是按需增长型以完成对输入的拓扑结构学习。

实际场景中，就是因为出现了大量输入参数的压缩和向量量化受阻的实际问题，比如语音与图像识别、抽象范式的分类与识别等。当输入不一致的，如果要进入深度神经网络DNN/CNN训练，是必须要进行裁剪压缩等处理，这可能会丢失一部分的输入数据的拓朴结构。

这里可以理解为PCA降维过程中，保留主要信息，但是破坏了原有特征间的联系，无法保持拓扑结构的问题。

自组织映射与赫布型学习已为人所知(尤其是生成网络拓扑即在神经元之间创建一系列连接，构成一个"框架"层的算法)，而且 “软” 竞争学习的方法亦已算出(在此类流程中，权重不仅适应"赢家"神经元，还适用其"近邻"神经元，本次竞争失败的神经元也要调整一下自己的参数，争取下次成功)，合理的步骤是将上述方法结合起来，而这已由德国科学家 Bernd Fritzke 于 1995 年完成，从而创建了如今的流行算法 “生长型神经气”(GNG)

GNG原文地址：
链接: https://proceedings.neurips.cc/paper/1994/hash/d56b9fc4b0f1be8871f5e1c40c0067e7-Abstract.html
此方法被证实非常成功，所以出现了一系列由其衍生的修改版本；其中之一就是监督式学习的改编适应版本 (Supervised-GNG)。勿庸置疑，GNG 要优于 “K-means” 聚类。

原始GNG

1. 创建两个节点，并初始化它们之间的连接边，将它们添加到图中。
2. 对于每个输入数据，找到离输入节点最近的两个节点。
3. 更新最近邻节点的位置和错误，以及连接最近邻节点和最近邻节点的邻居节点的边的年龄。
4. 如果最近邻的节点和次近邻的节点之间没有边连接，那么则在两个节点之间加一条边，然后将age置0，如果有连接也置零。
5. 如果当前的步数是lamda的倍数，且节点数没有达到最大值，则新建一个节点，将其加入到图中。
6. 对于所有节点的错误率进行衰减。
7. 如果需要，删除孤立节点和重要性参数较小的点。
8. 重复上述步骤，直到所有数据都被训练完毕。

一、GNG-A

链接: An adaptive algorithm for anomaly and novelty detection in evolving data streams

1.移除不相关神经元的机制

1. 定义局部变量 $C_n$： 对于每个神经元 $n$，引入了一个局部变量 $C_n$，用于估算移除该神经元的代价。$C_n$ 的值表示了如果移除神经元 $n$，那么与 $n$ 关联的数据点会被重新分配给其附近的神经元，从而导致附近神经元的总误差增加。因此，$C_n$ 的计算基于与神经元 $n$ 关联的数据点到其第二近的神经元的距离。

2. 计算 $C_n$： 公式中的 $C_n$ 表示为：
   $$C_n=\sum _{i=0}^{t}1(n=n_{x_i})\times |x_i-n_{x_i}^{\ast }|$$
   这里，$t$ 是当前时间步，$1(Cond)$ 是一个条件为真时为 1，否则为 0 的指示函数。这个公式的含义是，对于每个步数，当一个数据点与神经元 $n$ 关联时，$C_n$ 会增加该数据点到其第二近的神经元的距离。

3. 在线计算 $C_n$： 针对每个新接收的数据点 $x$，找到与其最近的神经元 $n_x^{\ast }$（即获胜神经元），然后将该神经元的 $C_{n_x^{\ast }}$ 值增加 $|x-n_x^{\ast }|$，表示了该数据点到其第二近的神经元的距离。

4. 指数衰减 $C_n$： 在每个迭代中，对所有现有的神经元，$C_n$ 会以指数方式减小：
   $$\forall n\in G,C_n\leftarrow 0.9\times C_n$$
   $C_n$ 随时间以指数速度衰减、

5. 决定移除神经元： 根据 $C_n$ 的值，可以判断神经元的相关性。当 $C_n$ 足够小时，可以触发遗忘机制，移除该神经元。但是，由于 $C_n$ 的值会快速接近 0，很难直接设置一个阈值。因此，提出了一个更方便的策略，即当 $-\log C_{\hat{n}}$ 足够高时触发移除操作，其中 $\hat{n}$ 是具有最小 $C_n$ 值的神经元，$\tau$ 是一个上限生存阈值。较小的 $\tau$ 会导致更快的遗忘，较大的 $\tau$ 会保留更长时间的记忆，具体阈值的选择取决于数据分布和其变化速度。

6. 自适应阈值 $\tau$： 为了确定 $\tau$ 的合适值，用自适应的方法

• 如果应该被移除$-\log C_{\hat{n}}>\tau$，则将 $\tau$ 以$$\tau \leftarrow \tau +ϵ\times \left[\left(-\log C_{r_{\dot{x}}^{\ast }}\right)-\tau \right],$$增加阈值；
• 如果不应该被移除$-\log C_{\hat{n}}>\tau$，则将 $\tau$ 以$$\tau \leftarrow \tau -ϵ\times \left[\left(-\log C_{r_{\dot{x}}^{\ast }}\right)-\tau \right],$$减小阈值；
  $ϵ$是一个0到1的很小的学习率，这个学习率也是随着步数逐渐减少达到收敛的：
  $$ϵ=\frac{1}{1+N_{\tau }}$$

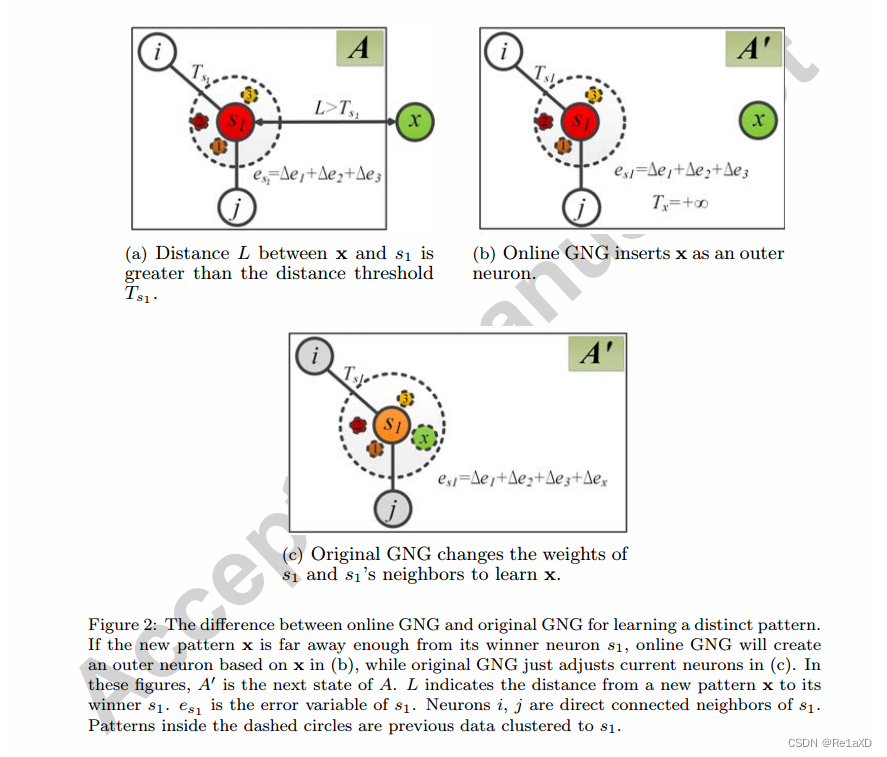
二、OGNG

链接: Online growing neural gas for anomaly detection in changing surveillance scenes

1.插入外部神经元

1. 在原始的GNG插入的基础上，增加外部插入的阈值，阈值计算为当前节点离所有邻居最远的距离
   

2.基于“密度”来删除神经元

• 先计算获胜节点离所有邻居的平均距离
• 然后计算分数（越稀疏分数越低） ${\text{ score }}_i=e^{-\overline{{\text{ dist }}_i}}$
• 计算总得分（每次都不停的累加），除以次数为平均得分$$a{s}_i=\sum _{k=1}^K\sum _{j=1}^{\lambda }{\text{ score }}_i(k,j)$$
• 最后删除分低的，基于阈值
• 阈值计算方法为，计算所有节点的分数，然后除以节点数量得到平均值当作阈值

三、GNG-T

链接: Following non-stationary distributions by controlling the vector quantization accuracy of a growing neural gas network

$$\begin{array}{rlr}\bar{E}i& =\int V_{i}d\left(\xi ,w_i\right)p\left(\xi /\xi \in V_i\right)\mathrm{d}\xi & =\left({\int }_{V_i}d\left(\xi ,w_i\right)p(\xi )\mathrm{d}\xi \right)/\left({\int }_{V_i}p(\xi )\mathrm{d}\xi \right).\end{array}$$

1. 原理：总误差$E$等于各部分误差项$E_i$的总和，当$E_i$的值趋于一个相同的值相等$T$时，总误差就达到最小。GNG-T的目标是通过控制这个$T$值，调整网络收敛到目标值。

2. 误差累积：当$w_i$作为获胜节点，输入样本为$\xi$时，它将样本$\xi$与自己的距离$d(w_i,\xi )$累积到一个累加器$e_i={\sum }_{1\le j\le n_i}d({\xi }_j^i,w_i)$中。这个累加误差$e_i$估计了$E_i$，即${\bar{E}}_i$的值。

3. 估算$E_i$：在一个包含N个样本的时期内，可以使用累加误差$e_i$来估算$E_i$。这可以表示为$E_i\approx \frac{e_i}{N}$。这个过程可以在每个原型上独立进行，但需要知道时期大小$N$。

4. 目标值$T$：GNG-T的核心思想是，当所有的$E_i$在平衡状态下都达到相同的值$T^{\prime }$时，将$T^{\prime }$与期望目标$T$进行比较。如果$T$小于$T^{\prime }$，则需要更多的神经元以提高量化的准确性。相反，如果$T$大于$T^{\prime }$，则当前的量化太精确，需要移除一些神经元。

5. $1/N$因子的去除：在原文中，$1/N$因子用于对计算进行规范化，使其与实际时期大小$N$无关。然而，为了处理非稳态分布，建议删除这个因子，以便更好地反映分布概率的变化。

6. 实现：GNG-T算法的实现是通过处理连续的时期来完成的。每个时期都开始于具有v个节点的图，这个图是前一次计算的结果。算法的主要步骤包括初始化、累积误差、更新权重、调整网络大小以使$e_i$接近$T$等。

GNG-T算法是一种用于自适应数据量化和聚类的算法，通过控制每个神经元的累积误差来实现对网络结构的自动调整，以适应不同的分布情况。这个算法的设计思想和步骤使得它适用于处理非稳态分布，并且提供了一个易于解释的目标值$T$来控制量化的准确性。

实验：动态阈值

$scor{e}_i=\frac{voting\_node\_scor{e}_i}{max\_voting\_node\_score}\times e^{-d_i}$

变量含义：

• $scor{e}_i$：第 $i$ 个投票节点的最终得分
• $voting\_node\_scor{e}_i$：第 $i$ 个投票节点的分数
• $max\_voting\_node\_score$：参与投票节点中最高的分数
• $d_i$：第 $i$ 个投票节点到当前数据点的欧氏距离

四、GNG-Ada中的loss

loss1计算公式：

$$loss1=\frac{1}{N}\sum _{i=1}^N{e}^{-\sqrt{winDis{t}_i}}$$

其中，$N$表示验证数据的数量，$winDis{t}_i$表示第$i$个验证数据的最近邻神经元的距离。

loss2计算公式：

$$loss2=\frac{1}{N}\sum _{i=1}^N\sqrt{winDis{t}_i}$$

其中，$N$表示验证数据的数量，$winDis{t}_i$表示第$i$个验证数据的最近邻神经元的距离。

$$diffLoss=loss1-loss2$$

• loss1中，测试集中数据应到最近邻神经元的欧式距离小，模型越好，欧式距离越小，负指数距离越大，平均负指数距离也越大，所以loss1越大越好；
• loss2中，同理，测试集中数据应到最近邻神经元的欧氏距离越小，模型越好，欧式距离越小，平均欧式距离也越小，所以loss2越小越好；
• 由于$diffLoss=loss1-loss2$，所以$diffloss$越大越好

五、bagging+集成学习+投票

1.权重的分配

当输入增量样本集 $D_i$ 时, 我们使用 ${\lambda }_m$ 来更新每个 RVM 的权重:
$$\begin{array}{rl}& P_m=\sum _{i=1}^{T}I\left(f_m\left(x_i^{\ast }\right)=t_i^{\ast }\right)/T\\ & {\lambda }_m=P_m/\sum _{m=1}^M{P}_m\end{array}$$

• $P_m$ 表示第 $m$ 个 RVM 的准确率，也就是在样本集 $D_i$ 上的正确率
• $I(\cdot )$ 是指示函数，当 $f_m(x_i^{\ast })=t_i^{\ast }$ 时取值为 $1$，否则取值为 $0$，只是函数的意思是预测准了就是1，不准就是0
• $T$ 表示样本集 $D_i$ 的大小
• ${\lambda }_m$ 表示第 $m$ 个 RVM 的权重，它是第 $m$ 个 RVM 准确率 $P_m$ 与所有 RVM 准确率之和的比值
  思路：先每个基学习器算一遍$P_m$，然后每个基学习器再算一遍${\lambda }_m$，通过投票法(或者说综合所有学习器性能来判断)来确定每个 RVM 的权重，使得准确率高的 RVM 在集成模型中占据更大的权重，从而提高集成模型的准确率。

2.动态重构的过程

为了对新的输入样本集 $D_i$ 获得更好的分类性能, 结合 RVM 的概率输出特性, 我们提出了评价基分类器好坏的一个性能指标总体错分概率权重值 $u_m$ 。定义为:
$$\begin{array}{rl}& u_m=\sum _{i=1}^T\left(1-p_m\left(f_m\left(x_i^{\ast }\right)=t_i^{\ast }\mid x_i^{\ast }\right)\right){\lambda }_m\\ & r=\underset{m}{\mathrm{argmax}}\left(u_m\right)\end{array}$$

这个公式是用来评价集成模型中每个基分类器的分类性能的。其中，$u_m$ 是错分概率权重和，表示每个基分类器 RVM 对于新的增量集的分类错误概率的加权和。

• $p_m(f_m(x_i^{\ast })=t_i^{\ast }|x_i^{\ast })$ 表示基分类器 RVM 对于样本 $x_i^{\ast }$ 的分类正确的概率，$t_i^{\ast }$ 是样本 $x_i^{\ast }$ 的真实标签，原来公式中用1减去$p_m$，说明公式中需要的是分类错误的概率（这个公式可能有错误，1-应该放在前面？）
• ${\lambda }_m$ 是基分类器 RVM 在集成模型中的权重（见 1.权重的分配）
• $r$ 是总体错分概率权重值最大的 RVM 的索引

思路：在动态增量更新阶段，寻找和删除性能最差的 RVM基学习器，同时在增量集上训练一个新的RVM。

3.集成决策输出

由：
$$F\left(x^{\ast }\right)=\underset{j}{\mathrm{argmax}}\left(\sum _{m=1}^M{\lambda }_{m}I\left(f_m\left(x^{\ast }\right)=j\right)\right)$$
变为：
$$F\left(x^{\ast }\right)=\underset{j}{\mathrm{argmax}}\left(\sum _{m=1}^M{\lambda }_m{p}_m\left(f_m\left(x^{\ast }\right)=j\mid x^{\ast }\right)\right)$$
思路：由用权重修正预测结果并求和取综合，变为权重加上正预测概率同时决定输出标签

问题：

1. 这个应用过程应该是一段一段的，而不是连续的，猜测：预训练之后进行应用，第一次增量正常>预测，第二次增量来的时候已经知道了第一次增量的标签结果，结合标签结果进行模型更新
2. 这个公式$p_m(f_m(x_i^{\ast })=t_i^{\ast }|x_i^{\ast })$，计算方法比较奇怪，正样本理论上来说是未知的，如果如同1中所说就没问题
3. 集成决策输出的部分也有类似的问题
4. RVM是相关向量机，用作分类训练的时候必须要有2个及2个以上的标签，我们的训练数据都是正常数据只有1个标签，RVM换成GNG也无法决定标签的种类总数$j$
5. 这个在输入时进行了降维，一般PCA将高维降维成2维度，但是新的数据流肯定是高维度，只有变为完整连续的数据集才能进行降维，侧面说明了数据是一段一段来的
6. 鲸鱼算法是优化超参的，这部分主要是提升指标凑篇幅

六、GNG降维可视化

链接: Scaling the Growing Neural Gas for Visual Cluster Analysis

• t-SNE降维+避免重叠边缘 结果

• 添加边时的策略，当a点和b点还没建立连接时需要满足：

1. a点和b点只有在它们有至少一个共同的邻居时才能连接。这样可以避免将远距离的节点连接起来，从而保留数据的局部结构。
2. a点和b点都分别与其它节点没有2条以上的边，避免了高维数据在低维空间中出现重叠的情况。
3. 如果存在两条边，则这两条边之间不能有连接。这样可以避免在低维空间中出现重叠的边缘。
4. 如果只有一条边，则连接两个节点的另一个节点最多只能与边有一个共同邻居，避免在低维空间中出现过于复杂的结构。
5. 次近邻获胜的节点必须属于一个小簇，这样可以保持数据的局部结构。

七、GWR

链接: A self-organising network that grows when required

初始化：

1. 初始化节点集合 A = { n 1 , n 2 } A=\left\{n_1, n_2\right\} A={n1​,n2​}，其中 $n_1,n_2$ 从输入分布 $p(\xi )$ 中随机初始化。
2. 初始化连接集合 $C=\varnothing$。

迭代过程（随数据流输入更新网络）：

1. 生成数据样本 $\mathbf{\xi }$ 作为网络的输入。

2. 对于网络中的每个节点 $i$，计算输入与节点权重向量的距离 $|\mathbf{\xi }-{\mathbf{w}}_i|$。

3. 选择最匹配的节点和次匹配的节点，即节点 $s,t\in A$，其中${\mathbf{w}}_n$是节点$n$的权重向量。
   $$s=\arg \underset{n\in A}{\min }\left|\mathbf{\xi }-{\mathbf{w}}_n\right|$$
   t = arg ⁡ min ⁡ n ∈ A ∖ { s } ∣ ξ − w n ∣ t=\arg \min _{n \in A \setminus \{s\}}\left|\boldsymbol{\xi}-\mathbf{w}_n\right| t=argn∈A∖{s}min​∣ξ−wn​∣

4. 如果 $s$ 和 $t$ 之间没有连接，则创建连接，否则，将连接的年龄设置为 0。
   $$C=C\cup \{(s,t)\}$$

5. 计算最匹配单元的活跃度（即e指数计算阈值）
   $$a=\exp \left(-|\mathbf{\xi }-{\mathbf{w}}_s|\right)$$

6. 如果$a<$阈值$a_{\mathrm{T}}$并且触发次数$h_{\mathrm{T}}$$<$触发阈值$h_{\mathrm{T}}$，则应在两个最匹配的节点$s$和$t$之间添加一个新节点$r$：

• 添加新节点$r$，创建新的权重向量，将权重设置为最匹配节点和输入向量的平均值：${\mathbf{w}}_r=\left({\mathbf{w}}_s+\xi \right)/2$。
• 在$r$和$s$之间以及$r$和$t$之间插入边：$C=C\cup (r,s),(r,t)$。
• 删除$s$和$t$之间的连接。

7. 如果未添加新节点，则调整获胜节点及其邻居的位置 $i$，即连接到它的节点：
   $$\begin{array}{rl}\Delta {\mathbf{w}}_s& ={ϵ}_b\times h_s\times (\xi -{\mathbf{w}}_s)\\ \Delta {\mathbf{w}}_i& ={ϵ}_n\times h_i\times (\xi -{\mathbf{w}}_i),\end{array}$$
   其中 $0<{ϵ}_n<{ϵ}_b<1$，$h_s$ 是节点 $s$ 触发次数。
8. 更新以 $s$ 为终点的边的年龄
   $$\mathrm{age}(s,i)=\mathrm{age}(s,i)+1$$
9. 根据以下公式减少获胜节点 $s$ 的 触发次数以及其邻居节点 $i$ 的 触发次数：
   $$\begin{array}{rl}{h}_s(t)& =h_0-\frac{S(t)}{{\alpha }_b}\left(1-{\mathrm{e}}^{-{\omega }_{3}t/x_b}\right)\\ h_i(t)& =h_0-\frac{S(t)}{{\alpha }_n}\left(1-{\mathrm{e}}^{-{\alpha }_n{\tau }_n}\right),\end{array}$$
   其中 $h_i(t)$ 是节点 $i$ 的触发变量的大小，$h_0$ 是初始，$S(t)$ 是强度，通常为1。${\alpha }_n,{\alpha }_b$ 和 ${\tau }_n,{\tau }_b$ 是控制曲线行为的常数。
10. 检查是否有要删除的节点或边，即是否有不再具有邻居的节点或年龄大于最大允许年龄的边，如果是，则删除它们（达到最大年龄、孤立点）。
11. 如果还有更多的输入可用，则返回到步骤（1）----数据流输入