[CF1491G]Switch and Flip

本文主要是介绍[CF1491G]Switch and Flip，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Switch and Flip

题解

我们可以先将原序列转化成一张有向图，点$i$向$\left|a_i\right|$连边。

我们的每次操作相当于交换两个点的出边所连向的点，并在两点颜色相同时将它们的颜色全部翻转。

相当于有这样的操作：

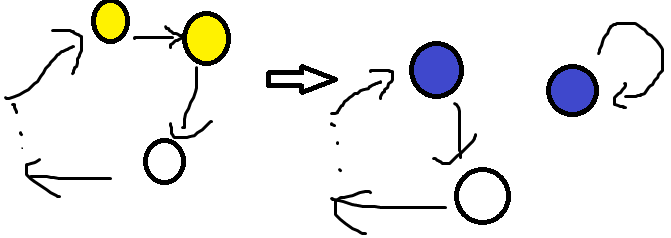
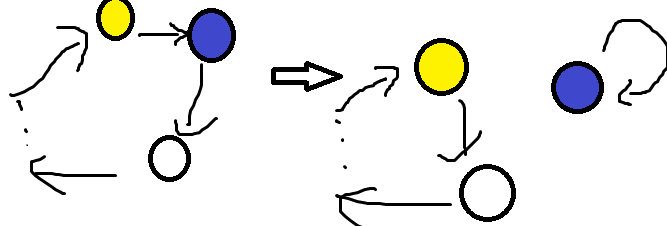
转化后的图必然有许多的环，我们的任务是将所有的环都变成自环。

如果我们有两个以上的环，我们有这样的解决方案：

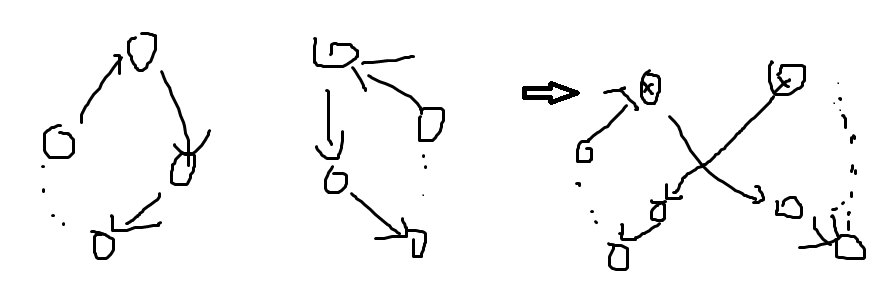
将两个环连在一起，然后通过操作不断缩小环的大小，将所有的为翻转点都变成自环，最后就只有两个反转点连成的环，用一次操作将它解决的，这样的操作数是$O\left(n\right)$的。

如果环数量最后不够，我们可以拿一个自环来代替，这样操作数是$O\left(n+1\right)$的。

但如果总共只有$1$个大小为$n$的环呢？

• 对于$n=2$的情况，直接翻一下就行了。

• 对于$n=3$的情况我们可以手玩一下，操作数是$O(4)$。

• 对于$n>3$的情况，我们可以先交换环上相邻的两个点，将其变成两个只有一个染色点的环。

  我们将其变成一个只有一个点染色的自环，一个有一个点染色一个点未染色的二元环。

  我们再交换这两个环上的点，将其转化成$n=3$的情况，照样处理即可。

  这样的操作数也是$O\left(n+1\right)$的。

总时间复杂度$O\left(n\right)$，毕竟都是处理环的翻转嘛。

源码

void dosaka(int u){vis[u]=1;vec[idx].push_back(u);if(!vis[c[u]])dosaka(c[u]);}
void Swap(int u,int v){swap(c[u],c[v]);ans.push_back(mkpr(u,v));}
signed main(){read(n);for(int i=1;i<=n;i++)read(c[i]);for(int i=1;i<=n;i++)if(!vis[i]&&c[i]!=i)idx++,dosaka(i);for(int i=2;i<=idx;i+=2){int u=vec[i][0],v=vec[i-1][0];Swap(u,v);while(c[u]!=v)Swap(u,c[u]);while(c[v]!=u)Swap(v,c[v]);Swap(u,v);}if(idx&1){if(vec[idx].size()<n){for(int i=1;i<=n;i++){if(c[i]!=i)continue;int u=vec[idx][0];Swap(i,u);while(c[i]!=u){int las=c[i];Swap(i,c[i]);}Swap(u,i);break;}}if(vec[idx].size()==n){if(n==2)Swap(vec[idx][0],vec[idx][1]);if(n==3){Swap(vec[idx][0],vec[idx][1]);Swap(vec[idx][1],vec[idx][2]);Swap(vec[idx][0],vec[idx][2]);Swap(vec[idx][0],vec[idx][1]);}if(n>3){Swap(vec[idx][0],vec[idx][1]);while(c[c[vec[idx][0]]]!=vec[idx][0])Swap(vec[idx][0],c[vec[idx][0]]);Swap(c[vec[idx][0]],vec[idx][1]);Swap(vec[idx][0],c[vec[idx][0]]);Swap(vec[idx][0],vec[idx][1]);}}}printf("%d\n",ans.size());for(int i=0;i<ans.size();i++)printf("%d %d\n",ans[i].fir,ans[i].sec);return 0;
}

谢谢！！！

这篇关于[CF1491G]Switch and Flip的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---