【C++ RB树】

2024-03-16 13:12
文章标签 c++ rb

本文主要是介绍【C++ RB树】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

    • 红黑树
      • 红黑树的概念
      • 红黑树的性质
      • 红黑树节点的定义
      • 红黑树的插入
      • 代码实现
      • 总结

红黑树

AVL树是一颗绝对平衡的二叉搜索树，要求每个节点的左右高度差的绝对值不超过1，这样保证查询时的高效时间复杂度O( l o g 2 N ) log_2 N) log2​N)，但是要维护其绝对平衡，旋转的次数比较多。因此，如果一颗树的结构经常修改，那么AVL树就不太合适，所以就有了红黑树。

红黑树的概念

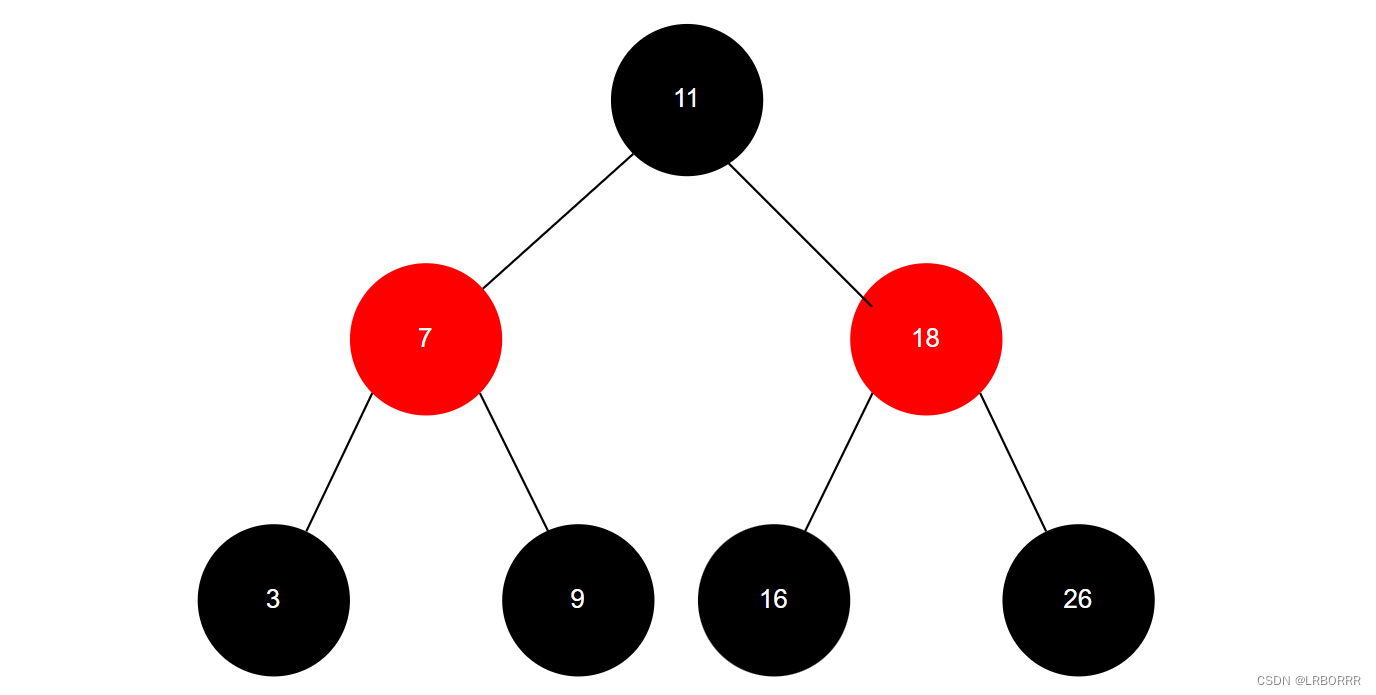
在这里插入图片描述
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。

红黑树的性质

  1. 每个节点不是红色就是黑色
  2. 根节点是黑色的
  3. 不存在连续的红色节点
  4. 任意一条从根到叶子的路径上的黑色节点的数量相同
    根据上面的性质，红黑树就可以确保没有一条路径会比其他路径长出两倍，因为每条路径上的黑色节点的数量相同，所以理论上最短边一定都是黑色节点，最长边一定是一黑一红的不断重复的路径。

红黑树节点的定义

	enum Color{RED,BLACK};template<class K, class V>struct RBTreeNode{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;pair<K, V> _kv;RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED),_kv(kv){}};

插入新节点的颜色一定是红色，因为如果新节点的颜色是黑色，那么每条路径上的黑色节点的数量就不相同了，处理起来就比较麻烦，所以宁愿出现连续的红色节点，也不能让某一条路径上多出一个黑色节点。

红黑树的插入

1.根据二叉搜索树的规则插入新节点

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* curr = _root;Node* parent = nullptr;while (curr){if (curr->_kv.first < kv.first){parent = curr;curr = curr->_right;}else if (curr->_kv.first > kv.first){parent = curr;curr = curr->_left;}else{return false;}}curr = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = curr;elseparent->_left = curr;curr->_parent = parent;
........

2.测新节点插入后，红黑树的性质是否造到破坏

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* curr = _root;Node* parent = nullptr;while (curr){if (curr->_kv.first < kv.first){parent = curr;curr = curr->_right;}else if (curr->_kv.first > kv.first){parent = curr;curr = curr->_left;}else{return false;}}curr = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = curr;elseparent->_left = curr;curr->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;curr = grandfather;parent = curr->_parent;}else{if (curr == parent->_left){//      g//   p     u//cRotatoR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g//   p     u//    cRotatoL(parent);RotatoR(grandfather);curr->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;curr = grandfather;parent = curr->_parent;}else{if (curr == parent->_right){//      g   //   u     p//           cRotatoL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g   //   u     p//        cRotatoR(parent);RotatoL(grandfather);curr->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}
void RotatoL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subR;elseppnode->_right = subR;subR->_parent = ppnode;}
}
void RotatoR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subL;elseppnode->_right = subL;subL->_parent = ppnode;}
}

代码实现

#pragma once
#include <utility>namespace lw
{enum Color{RED,BLACK};template<class K, class V>struct RBTreeNode{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;pair<K, V> _kv;RBTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED),_kv(kv){}};template<class K, class V>class RBTree{typedef RBTreeNode<K, V> Node;public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* curr = _root;Node* parent = nullptr;while (curr){if (curr->_kv.first < kv.first){parent = curr;curr = curr->_right;}else if (curr->_kv.first > kv.first){parent = curr;curr = curr->_left;}else{return false;}}curr = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = curr;elseparent->_left = curr;curr->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;curr = grandfather;parent = curr->_parent;}else{if (curr == parent->_left){//      g//   p     u//cRotatoR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g//   p     u//    cRotatoL(parent);RotatoR(grandfather);curr->_col = BLACK;grandfather->_col = RED;}break;}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;curr = grandfather;parent = curr->_parent;}else{if (curr == parent->_right){//      g   //   u     p//           cRotatoL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//      g   //   u     p//        cRotatoR(parent);RotatoL(grandfather);curr->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotatoL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subR;elseppnode->_right = subR;subR->_parent = ppnode;}}void RotatoR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent)ppnode->_left = subL;elseppnode->_right = subL;subL->_parent = ppnode;}}void InOrder(){_InOrder(_root);}bool IsBalance(){if (_root && _root->_col == RED)return false;Node* left = _root;int count = 0;while (left){if (left->_col == BLACK)count++;left = left->_left;}return check(_root, 0, count);}private:bool check(Node* root, int count, int refBlackNumber){if (root == nullptr){if (count == refBlackNumber)return true;elsereturn false;}if (root->_col == RED && root->_parent->_col == RED)return false;if (root->_col == BLACK)count++;return check(root->_left, count, refBlackNumber)&& check(root->_right, count, refBlackNumber);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " : " << root->_kv.second << endl;_InOrder(root->_right);}Node* _root = nullptr;};
}

总结

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O( l o g 2 N log_2 N log2​N)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

这篇关于【C++ RB树】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/815605。

相关文章

C++如何通过Qt反射机制实现数据类序列化

C++如何通过Qt反射机制实现数据类序列化

《C++如何通过Qt反射机制实现数据类序列化》在C++工程中经常需要使用数据类,并对数据类进行存储、打印、调试等操作,所以本文就来聊聊C++如何通过Qt反射机制实现数据类序列化吧... 目录设计预期设计思路代码实现使用方法在 C++ 工程中经常需要使用数据类，并对数据类进行存储、打印、调试等操作。由于数据类
阅读更多...
Linux下如何使用C++获取硬件信息

Linux下如何使用C++获取硬件信息

《Linux下如何使用C++获取硬件信息》这篇文章主要为大家详细介绍了如何使用C++实现获取CPU,主板,磁盘,BIOS信息等硬件信息,文中的示例代码讲解详细,感兴趣的小伙伴可以了解下... 目录方法获取CPU信息：读取"/proc/cpuinfo"文件获取磁盘信息：读取"/proc/diskstats"文
阅读更多...
C++使用printf语句实现进制转换的示例代码

C++使用printf语句实现进制转换的示例代码

《C++使用printf语句实现进制转换的示例代码》在C语言中,printf函数可以直接实现部分进制转换功能,通过格式说明符（formatspecifier）快速输出不同进制的数值,下面给大家分享C+... 目录一、printf 原生支持的进制转换1. 十进制、八进制、十六进制转换2. 显示进制前缀3. 指
阅读更多...
C++中初始化二维数组的几种常见方法

C++中初始化二维数组的几种常见方法

《C++中初始化二维数组的几种常见方法》本文详细介绍了在C++中初始化二维数组的不同方式,包括静态初始化、循环、全部为零、部分初始化、std::array和std::vector,以及std::vec... 目录1. 静态初始化2. 使用循环初始化3. 全部初始化为零4. 部分初始化5. 使用 std::a
阅读更多...
C++ vector的常见用法超详细讲解

C++ vector的常见用法超详细讲解

《C++vector的常见用法超详细讲解》：本文主要介绍C++vector的常见用法,包括C++中vector容器的定义、初始化方法、访问元素、常用函数及其时间复杂度,通过代码介绍的非常详细,... 目录1、vector的定义2、vector常用初始化方法1、使编程用花括号直接赋值2、使用圆括号赋值3、ve
阅读更多...
如何高效移除C++关联容器中的元素

如何高效移除C++关联容器中的元素

《如何高效移除C++关联容器中的元素》关联容器和顺序容器有着很大不同,关联容器中的元素是按照关键字来保存和访问的,而顺序容器中的元素是按它们在容器中的位置来顺序保存和访问的,本文介绍了如何高效移除C+... 目录一、简介二、移除给定位置的元素三、移除与特定键值等价的元素四、移除满足特android定条件的元
阅读更多...
Python获取C++中返回的char*字段的两种思路

Python获取C++中返回的char*字段的两种思路

《Python获取C++中返回的char*字段的两种思路》有时候需要获取C++函数中返回来的不定长的char*字符串,本文小编为大家找到了两种解决问题的思路,感兴趣的小伙伴可以跟随小编一起学习一下... 有时候需要获取C++函数中返回来的不定长的char*字符串，目前我找到两种解决问题的思路，具体实现如下：
阅读更多...
C++ Sort函数使用场景分析

C++ Sort函数使用场景分析

《C++Sort函数使用场景分析》sort函数是algorithm库下的一个函数,sort函数是不稳定的,即大小相同的元素在排序后相对顺序可能发生改变,如果某些场景需要保持相同元素间的相对顺序,可使... 目录C++ Sort函数详解一、sort函数调用的两种方式二、sort函数使用场景三、sort函数排序
阅读更多...
Java调用C++动态库超详细步骤讲解(附源码)

Java调用C++动态库超详细步骤讲解(附源码)

《Java调用C++动态库超详细步骤讲解(附源码)》C语言因其高效和接近硬件的特性,时常会被用在性能要求较高或者需要直接操作硬件的场合,：本文主要介绍Java调用C++动态库的相关资料,文中通过代... 目录一、直接调用C++库第一步：动态库生成（vs2017+qt5.12.10）第二步：Java调用C++
阅读更多...
C/C++错误信息处理的常见方法及函数

C/C++错误信息处理的常见方法及函数

《C/C++错误信息处理的常见方法及函数》C/C++是两种广泛使用的编程语言,特别是在系统编程、嵌入式开发以及高性能计算领域,：本文主要介绍C/C++错误信息处理的常见方法及函数,文中通过代码介绍... 目录前言1. errno 和 perror()示例：2. strerror()示例：3. perror(
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2