旋转门压缩算法(SDT)的Go实现

原理

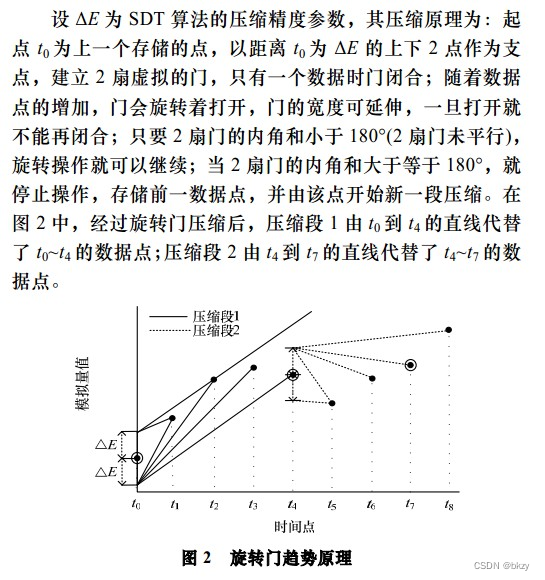
实质上，是计算门轴到新数据点之间线段的斜率，门轴既是线段的零点。由于直线段的公式为：

x = kt+b //k为斜率,b为0点,t为时间轴,x为数据大小

上下门轴点的计算方法为：

ub=x0+ΔE //上门轴，x0为存储点的数值
db=x0-ΔE //下门轴，x0为存储点的数值

上下门斜率的计算方法为：

uk=(xt-ub)/Δt //上门斜率
dk=(xt-db)/Δt //下门斜率

在t0点，门关闭，上门斜率无线小，下门斜率无限大。随着时间轴的右伸，上门斜率逐渐变大(单向，只能变大)，下门斜率逐渐变小(单向,只能变小)。当上门斜率大于等于下门斜率时，保存前一个数据点。
具体流程为：

算法的实现

package modelsimport ("time"
)//旋转门压缩结构体
type SdtDoor struct {DeltaE         float64   //门初始宽度LastHisV       float64   //上一次存储的数据值LastHisT       time.Time //上一次存储的数据时间戳LastRealV      float64   //上一次的实时数据值LastRealT      time.Time //上一次实时数据的时间戳MaxIntervalSec int64     //数据存储最大间隔秒数isinit         bool      //初始化状态closed         bool      //初始关门状态uk             float64   //上斜率dk             float64   //下斜率ub             float64   //上零点db             float64   //下零点
}//新建旋转门压缩实体
func NewSdtDoor(deltaE float64, maxsec int64) *SdtDoor {sdt := &SdtDoor{DeltaE: deltaE, MaxIntervalSec: maxsec, closed: true, isinit: true}return sdt
}//旋转门过滤器
func (sdt *SdtDoor) Filter(pointV float64, pointT time.Time) bool {if sdt.DeltaE == 0 { //门宽度为零return true //保存每一个数据}save := false   //过滤检查结果if sdt.isinit { //初始化状态sdt.isinit = falsesave = true} else {deltaT := float64(pointT.Sub(sdt.LastHisT).Milliseconds())//fmt.Printf("时间差:%fms\n", deltaT)if sdt.closed { //开门第一个点if deltaT > 0 {sdt.closed = falsesdt.uk = (pointV - sdt.ub) / deltaTsdt.dk = (pointV - sdt.db) / deltaT}} else {uk := (pointV - sdt.ub) / deltaTdk := (pointV - sdt.db) / deltaTif uk > sdt.uk { //上斜率只保存增大的sdt.uk = uk}if dk < sdt.dk { //下斜率只保存减小的sdt.dk = dk}if sdt.dk <= sdt.uk { //下斜率小于等于上斜率,触发保存save = true}if !save {if deltaT/1000.0 > float64(sdt.MaxIntervalSec) { //已经长时间没有触发保存save = true}}}}if save {sdt.LastHisV = sdt.LastRealVsdt.LastHisT = sdt.LastRealTsdt.ub = sdt.LastHisV + sdt.DeltaEsdt.db = sdt.LastHisV - sdt.DeltaEsdt.closed = true}sdt.LastRealV = pointVsdt.LastRealT = pointTreturn save
}

测试用例

func TestSdt(t *testing.T) {deltaE := 0.005 //门宽,即压缩精度datas := []struct {tstamp int64   //时间戳,UNIX秒sinv   float64 //正玄波值}{{1651800000, 0},{1651800001, 0.0998334166468282},{1651800002, 0.198669330795061},{1651800003, 0.29552020666134},{1651800004, 0.389418342308651},{1651800005, 0.479425538604203},{1651800006, 0.564642473395035},{1651800007, 0.644217687237691},{1651800008, 0.717356090899523},{1651800009, 0.783326909627483},{1651800010, 0.841470984807897},{1651800011, 0.891207360061435},{1651800012, 0.932039085967226},{1651800013, 0.963558185417193},{1651800014, 0.98544972998846},{1651800015, 0.997494986604054},{1651800016, 0.999573603041505},{1651800017, 0.991664810452469},{1651800018, 0.973847630878195},{1651800019, 0.946300087687414},{1651800020, 0.909297426825682},{1651800021, 0.863209366648874},{1651800022, 0.80849640381959},{1651800023, 0.74570521217672},{1651800024, 0.675463180551151},{1651800025, 0.598472144103956},{1651800026, 0.515501371821464},{1651800027, 0.427379880233829},{1651800028, 0.334988150155904},{1651800029, 0.239249329213982},{1651800030, 0.141120008059866},{1651800031, 0.0415806624332896},{1651800032, -0.058374143427581},{1651800033, -0.15774569414325},{1651800034, -0.255541102026833},{1651800035, -0.350783227689621},{1651800036, -0.442520443294854},{1651800037, -0.529836140908495},{1651800038, -0.61185789094272},{1651800039, -0.687766159183975},{1651800040, -0.756802495307929},{1651800041, -0.818277111064411},{1651800042, -0.871575772413589},{1651800043, -0.916165936749456},{1651800044, -0.951602073889517},{1651800045, -0.977530117665097},{1651800046, -0.993691003633465},{1651800047, -0.999923257564101},{1651800048, -0.99616460883584},{1651800049, -0.982452612624332},{1651800050, -0.958924274663138},{1651800051, -0.925814682327731},{1651800052, -0.883454655720152},{1651800053, -0.8322674422239},{1651800054, -0.772764487555985},{1651800055, -0.705540325570389},{1651800056, -0.631266637872319},{1651800057, -0.550685542597635},{1651800058, -0.464602179413754},{1651800059, -0.373876664830233},{1651800060, -0.279415498198922},{1651800061, -0.182162504272092},{1651800062, -0.0830894028174929},{1651800063, 0.0168139004843542},{1651800064, 0.116549204850497},{1651800065, 0.215119988087819},{1651800066, 0.311541363513382},{1651800067, 0.404849920616602},{1651800068, 0.494113351138612},{1651800069, 0.578439764388203},{1651800070, 0.656986598718792},{1651800071, 0.72896904012588},{1651800072, 0.793667863849156},{1651800073, 0.850436620628567},{1651800074, 0.898708095811629},{1651800075, 0.937999976774741},{1651800076, 0.967919672031488},{1651800077, 0.988168233877001},{1651800078, 0.998543345374605},{1651800079, 0.998941341839772},{1651800080, 0.989358246623381},{1651800081, 0.969889810845085},{1651800082, 0.940730556679771},{1651800083, 0.902171833756291},{1651800084, 0.854598908088278},{1651800085, 0.798487112623487},{1651800086, 0.73439709787411},{1651800087, 0.662969230082178},{1651800088, 0.584917192891757},{1651800089, 0.50102085645788},{1651800090, 0.412118485241752},{1651800091, 0.319098362349347},{1651800092, 0.222889914100242},{1651800093, 0.124454423507058},{1651800094, 0.0247754254533542},}sdt := NewSdtDoor(deltaE, 100)for i, dt := range datas {t := time.Unix(dt.tstamp, 0)save := sdt.Filter(dt.sinv, t)//fmt.Printf("%d uk=%f,dk=%f,diff=%f,save=%t\n", i, sdt.uk, sdt.dk, sdt.uk-sdt.dk, save)if save {if i == 0 {fmt.Println(dt)} else {if i != 1 { //第一个数前面已经输出过了，不再重复fmt.Println(datas[i-1])}}}}
}

测试结果

{1651800000 0}
{1651800001 0.0998334166468282}
{1651800005 0.479425538604203}
{1651800008 0.717356090899523}
{1651800011 0.891207360061435}
{1651800013 0.963558185417193}
{1651800015 0.997494986604054}
{1651800017 0.991664810452469}
{1651800019 0.946300087687414}
{1651800021 0.863209366648874}
{1651800024 0.675463180551151}
{1651800027 0.427379880233829}
{1651800032 -0.058374143427581}
{1651800036 -0.442520443294854}
{1651800039 -0.687766159183975}
{1651800042 -0.871575772413589}
{1651800044 -0.951602073889517}
{1651800046 -0.993691003633465}
{1651800048 -0.99616460883584}
{1651800050 -0.958924274663138}
{1651800052 -0.883454655720152}
{1651800055 -0.705540325570389}
{1651800058 -0.464602179413754}
{1651800062 -0.0830894028174929}
{1651800067 0.404849920616602}
{1651800070 0.656986598718792}
{1651800073 0.850436620628567}
{1651800075 0.937999976774741}
{1651800077 0.988168233877001}
{1651800079 0.998941341839772}
{1651800081 0.969889810845085}
{1651800083 0.902171833756291}
{1651800086 0.73439709787411}
{1651800089 0.50102085645788}
{1651800093 0.124454423507058}

对上述测试数据绘图

参考文献

SDT旋转门压缩算法MFC图形测试
数据压缩算法：旋转门算法（SDT）的C#实现