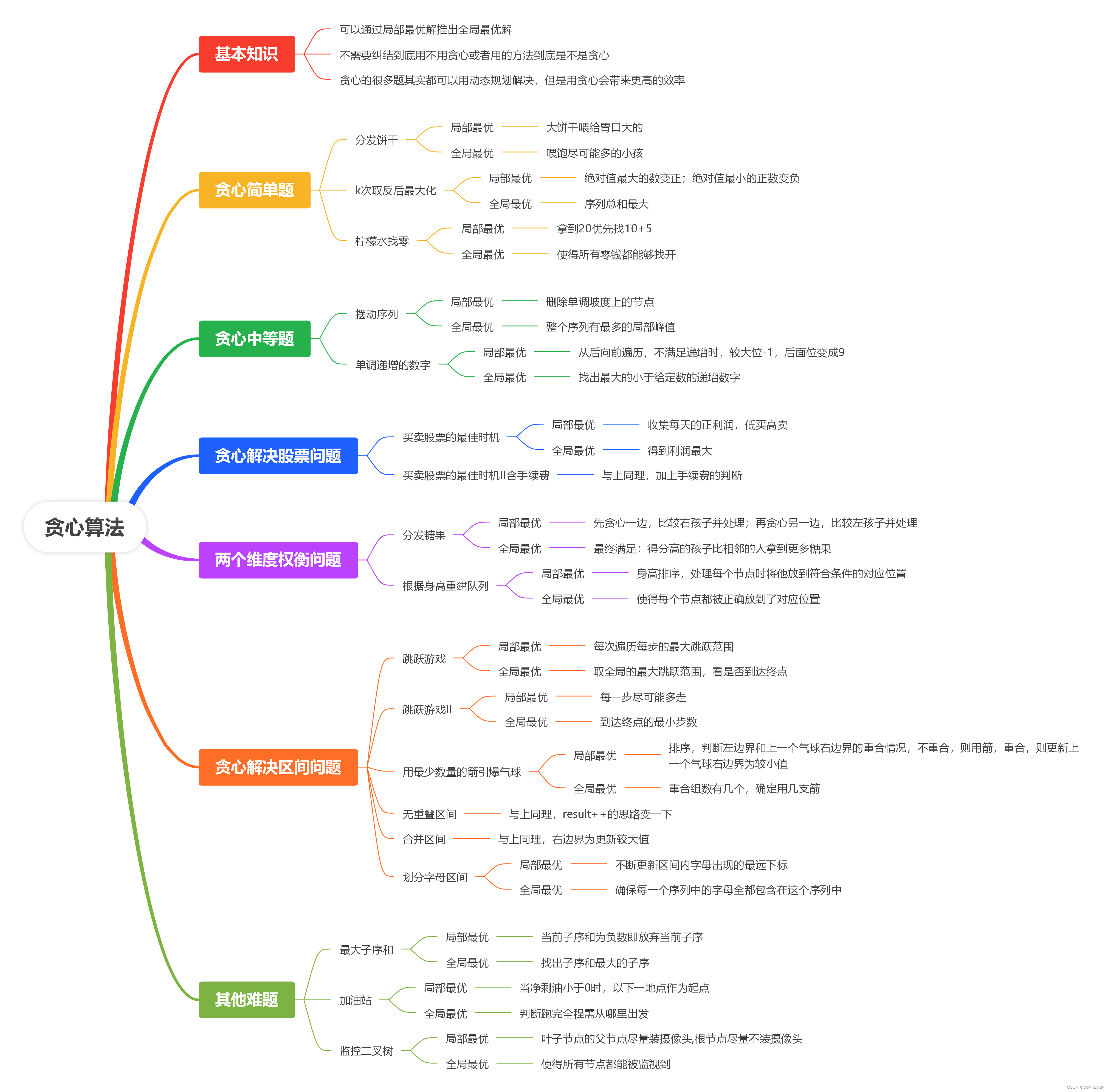
本文主要是介绍monotoneIncreasingDigits-LeetCode738,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目要求
给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。
(当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。)
示例 1:
输入: N = 10
输出: 9
示例 2:
输入: N = 1234
输出: 1234
示例 3:
输入: N = 332
输出: 299
说明: N 是在 [0, 10^9] 范围内的一个整数。
Related Topics 贪心算法
解题思路(欠着,后补)
代码
public int monotoneIncreasingDigits(int N) {//解题思路判断这个数值是否是按照递增的顺序排列的String RN=N+"";if(RN.length()==1)return N;StringBuilder sb=new StringBuilder();if(RN.charAt(0)=='1'&&RN.charAt(1)=='0'){for (int i = 1; i < RN.length(); i++) {sb.append(9);}return Integer.parseInt(sb.toString());}int k=RN.length()+1;for (int i = 1; i < RN.length(); i++) {if(RN.charAt(i)-'0'>=RN.charAt(i-1)-'0'){sb.append(RN.charAt(i-1)-'0');if(i== RN.length()-1)sb.append(RN.charAt(i)-'0');continue;}if(sb.length()>0&&RN.charAt(i-1)==RN.charAt(i-2)){int index = sb.indexOf(String.valueOf(RN.charAt(i - 1) - '0'));sb.replace(index,index, String.valueOf(RN.charAt(index)-'0'-1));sb.delete(index+1,sb.length());k=index+1;}else{sb.append(RN.charAt(i-1)-'0'-1);k=i;}break;}for (int i = k; i < RN.length(); i++) {sb.append(9);}return Integer.parseInt(sb.toString());}
效果(后续参考大神解法,插眼等后续):
info
解答成功:
执行耗时:8 ms,击败了11.20% 的Java用户
内存消耗:35.6 MB,击败了40.36% 的Java用户
这篇关于monotoneIncreasingDigits-LeetCode738的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!