曲线拟合基础知识

本文主要是介绍曲线拟合基础知识，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 介绍最小二乘法：           最小二乘法（Least Squares）简介-CSDN博客

     例如下图，找到一个方程，此方程要满足：把每个点带入计算得到的 预测结果 与 实际结果 的误差(残差)的平均值越小越好。如下红色线就是找到的方程，找这个方程的方法可以用 最小二乘法

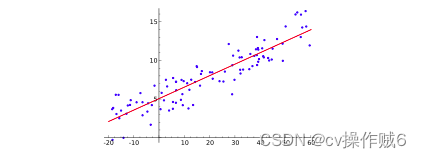
最小二乘法，为什么叫二乘法？

​二乘其实是指平方的意思，为什么用平方呢？因为平方可以消除误差正负方向上的差异，单纯的只比较长度。

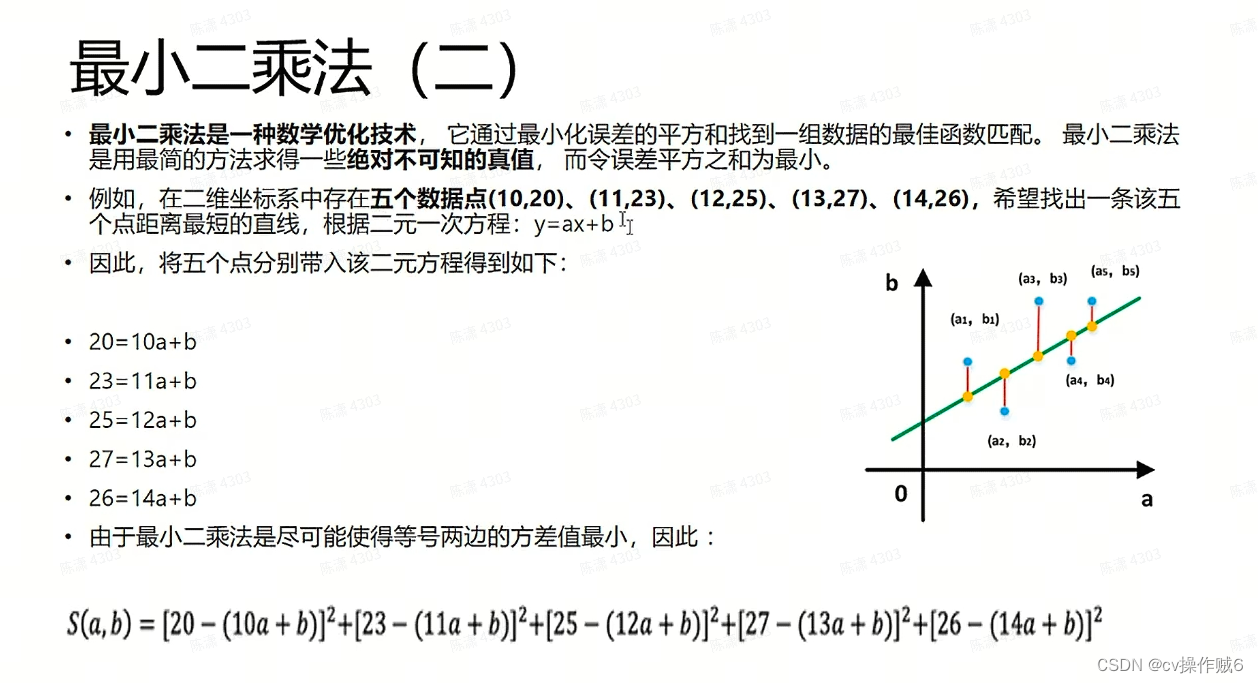
最小二乘法主要包含了两大类方法，一种是线性最小二乘法（Linear Least Squares），一种是非线性最小二乘法（Nonlinear Least Squares）。

slam第六讲 http://admin.guyuehome.com/41198

---

曲线拟合 实现 一 基于最小二乘法的多项式曲线拟合：从原理到c++实现 - 知乎

#include <iostream>                   //输入输出头文件
#include <opencv2/core/core.hpp>     //opencv核心代码头文件
#include <ceres/ceres.h>            //ceres 头文件
#include <chrono>                  //计时用using namespace std;
//假设输入的数据为 (1, 2)  (2, 3)  (3, 4)  (4, 5) //用于存储构建线性方程组的《系数矩阵》 向量 B 被用于存储构建线性方程组的《常数向量》//矩阵A例子如下//  [ 4         10         30         100        4对应常数项系数//    10        30         100        354        4900对应三次项系数//    30        100        354        1300       //    100       354        1300       4900]      //矩阵B为// B = | 14 |//     | 42 |//     | 130|//     | 500|
// 拟合结果（coeff）为：  对应的方程为 y = -28 * x^0 + 66.5 * x + (-36.5) * x^2 + 5.5 * x^3
// coeff = [[-28],
// [ 66.5],
// [-36.5],
// [ 5.5]]//代数方式求解  order多项式的阶数，即拟合曲线的最高次幂   coeff指向输出参数（拟合曲线的系数）的指针。这是一个 cv::Mat 对象，将被用于存储计算得到的系数
void PolyFit(const std::vector<cv::Point2f> &points, const int order,cv::Mat *coeff) 
{const int n = points.size();cv::Mat A = cv::Mat::zeros(order + 1, order + 1, CV_64FC1);//矩阵 A 初始化为大小为 (order + 1) x (order + 1) 的零矩阵,   CV_64FC1表示双精度cv::Mat B = cv::Mat::zeros(order + 1, 1, CV_64FC1);//初始化为大小为 (order + 1) x 1 的零向量   《结果向量 B 即常数向量》
//已知order == 3// 构建A矩阵for (int i = 0; i < order + 1; ++i) {for (int j = 0; j < order + 1; ++j) {for (int k = 0; k < n; ++k) //遍历输入点集{A.at<double>(i, j) += std::pow(points.at(k).x, i + j);// 累加所有点的 x的(i+j)次幂 }}}// 构建B矩阵for (int i = 0; i < order + 1; ++i) {for (int k = 0; k < n; ++k) {B.at<double>(i, 0) += std::pow(points.at(k).x, i) * points.at(k).y;//B = [所有x的0次方的累加和 * y ，所有x的1次方的累加和 * y，所有x的2次方的累加和 * y，所有x的3次方的累加和 * y]}}//通过求解线性方程组 A * coeff = B，得到多项式的系数 coeff(*coeff) = cv::Mat::zeros(order + 1, 1, CV_64FC1);//4x1的零矩阵// 求解 通过解线性方程组得到多项式拟合的系数，并将结果存储在 *coeff 中if (!cv::solve(A, B, *coeff, cv::DECOMP_LU)) {std::cout << "Failed to solve !" << std::endl;}
}
// 矩阵方式求解
void PolyFit(const std::vector<cv::Point2f> &points, const int order,cv::Mat *coeff) {cv::Mat A = cv::Mat::ones(n, order + 1, CV_64FC1);cv::Mat B = cv::Mat::zeros(n, 1, CV_64FC1);for (int i = 0; i < n; ++i) {const double a = points.at(i).x;const double b = points.at(i).y;B.at<double>(i, 0) = b;for (int j = 0, v = 1.0; j < order + 1; ++j, v *= a) {A.at<double>(i, j) = v;}}// 使用cv::solve求解(A^T * A) * coeff = A^T * Bcv::Mat At = A.t();cv::Mat AtA = At * A;cv::Mat AtB = At * B;cv::solve(AtA, AtB, *coeff, cv::DECOMP_NORMAL);
}
float PolyValue(const cv::Mat &coeff, const int order, const float x) {float v = 0;for (int i = 0; i < order; ++i) {v += coeff.at<double>(i, 0) * std::pow(x, i);}return v;
}int main(int argc, char **argv) {constexpr int kOrder = 3; // 多项式阶数constexpr int kWidth = 1000;constexpr int kHeight = 500;cv::Mat canvas =cv::Mat(cv::Size(kWidth, kHeight), CV_8UC3, cv::Scalar(255, 255, 255));cv::RNG rng(0xFFFFFFFF); // 随机数// 生成点集，y坐标添加一些随机噪声std::vector<cv::Point2f> raw_points;for (int i = 10; i < kWidth; i += 10) {cv::Point2f p;p.x = i;const auto noise = rng.uniform(-kHeight / 10, kHeight / 10);p.y = kHeight - p.x / kWidth * kHeight + noise;cv::circle(canvas, p, 5, cv::Scalar(0, 0, 255), -1);raw_points.emplace_back(p);}// 多项式拟合cv::Mat coeff;PolyFit(raw_points, kOrder, &coeff);// 用拟合后的系数重新生成点集std::vector<cv::Point> poly_points;for (const auto &rp : raw_points) {cv::Point p;p.x = rp.x;p.y = PolyValue(coeff, kOrder, rp.x);cv::circle(canvas, p, 5, cv::Scalar(0, 255, 0), -1);poly_points.emplace_back(p);}cv::polylines(canvas, poly_points, false, cv::Scalar(0, 255, 0), 3,cv::LINE_4);cv::imshow("PolyFit", canvas);cv::waitKey(0);cv::destroyAllWindows();return 0;
}

这篇关于曲线拟合基础知识的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---