Leedcode刷题——5 DFS+回溯

2024-03-13 16:04
文章标签 刷题 dfs 回溯 leedcode

本文主要是介绍Leedcode刷题——5 DFS+回溯，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

注：以下代码均为c++

1. 电话号码的字母组合

在这里插入图片描述
思路：
在这里插入图片描述
例如：”23“
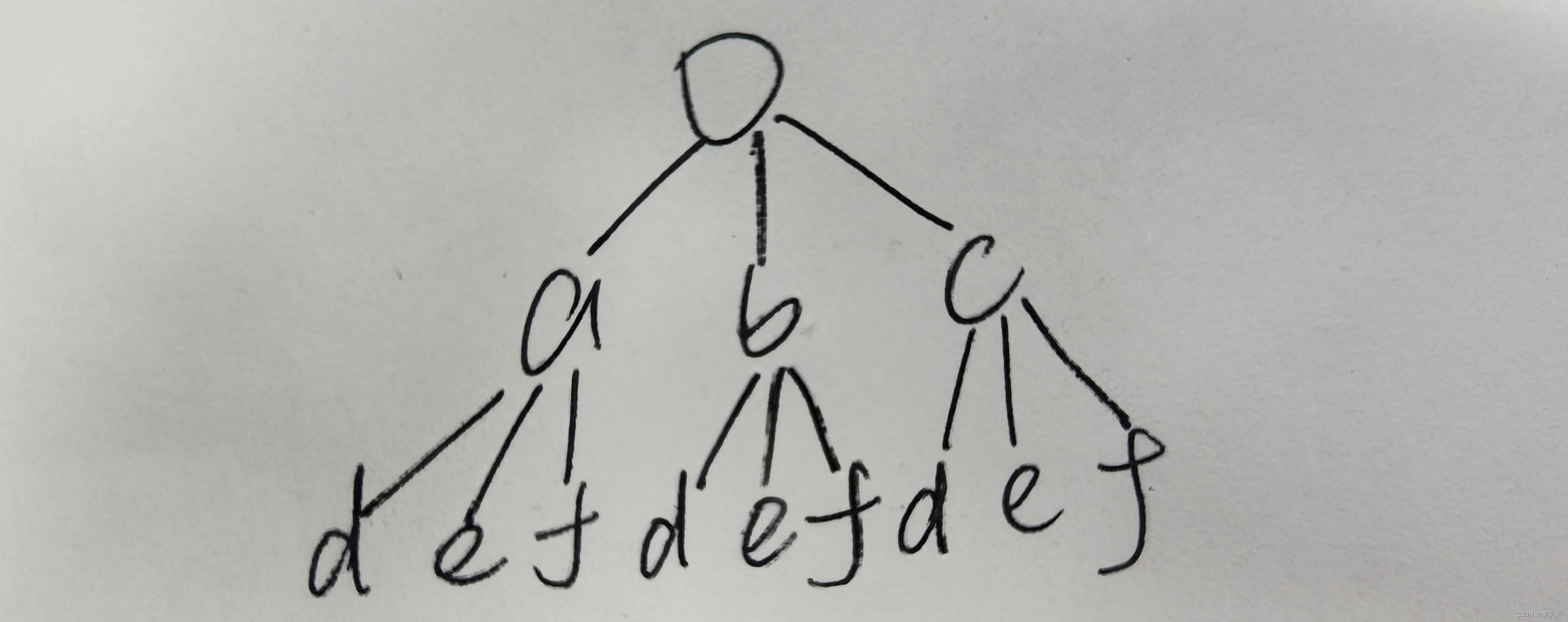
请添加图片描述

在这里插入图片描述

//1. 我自己写的
vector<string> letterCombinations(string digits) {if(digits == "")return {};vector<string> state = {""};string s;vector<string> strs = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};for(int i = 0; i < digits.size(); i++){s = strs[digits[i] - '0'];  //"abc"vector<string> state_new = {};for(int j = 0; j < s.size(); j++){for(int t = 0; t < state.size(); t++){string sta = state[t] + s[j];state_new.push_back(sta);}}state = state_new;}return state;
}//2. 答案
//把循环换种方式写
string strs[8] = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector<string> letterCombinations(string digits){if(digits == "")  return vector<string>();vector<string> state = {""};for(auto u: digits){vector<string> now;for(auto c: strs[u-'2']){for(auto s: state)now.push_back(s+c);}state = now;}return state;
}

2. 单词搜索

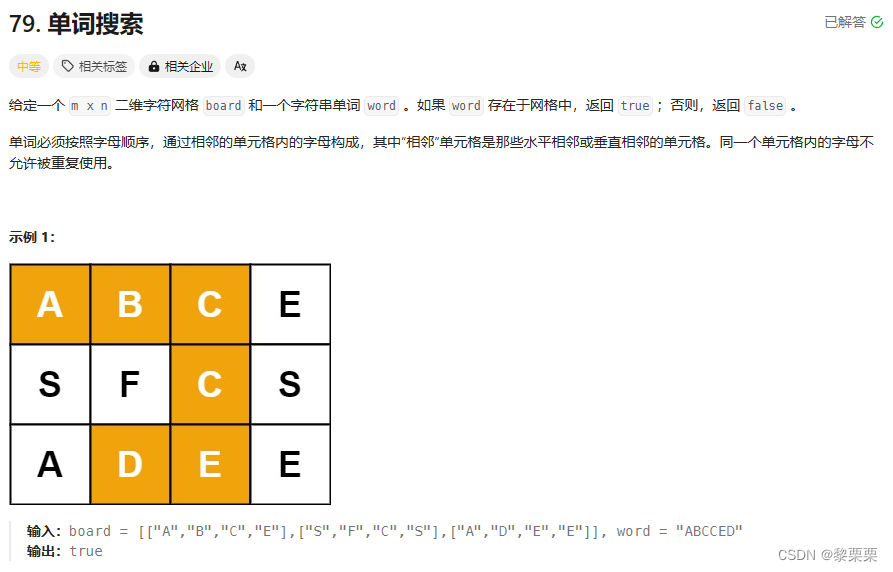
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
思路：
在这里插入图片描述

int n, m;  //行，列
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};  //dx为行加的距离，dy为列加的距离。四位分别表示为：上右下左bool dfs(vector<vector<char>> &board, int i, int j, string &word,int u) {  //注：这里的board传引用的原因是：每搜索过一个元素后，我们需要修改board的值，对其进行标记。if (board[i][j] != word[u]) return false;if (u == word.size() - 1) return true;board[i][j] = '.';  //如果搜索过了，进行标记//依次搜索下一点的位置（上下左右）for (int k = 0; k < 4; k++) {int x = i + dx[k], y = j + dy[k];if (x >= 0 && x < n && y >= 0 && y < m)if (dfs(board, x, y, word, u + 1))return true;}//当上下左右都搜索完一遍后，将标记点复原。board[i][j] = word[u];return false;
}bool exist(vector<vector<char>> &board, string word) {  //为什么传引用？因为不传引用会复制一遍整个数组，浪费时间。if (board.empty() || board[0].empty()) return false;n = board.size(), m = board[0].size();//1 枚举起点for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)if (dfs(board, i, j, word, 0))  //字符网格，枚举起点的位置，搜索单词，搜索单词位置return true;return false;
}

3. 全排列

在这里插入图片描述
思路：
在这里插入图片描述
法1：枚举每个位置放哪个数
我们定义递归函数 dfs(vector& nums, int u) 表示输入数组为 nums，下一个待填入的位置是第u个位置（下标从 0 开始）。定义vector num;表示当前排列。那么整个递归函数分为两个情况：

  1. 如果 u=n，说明我们已经填完了 n 个位置，找到了一个可行的解，我们将 num 放入答案数组中，递归结束。
  2. 如果u<n，我们要考虑第u 个位置填哪个数。根据题目要求我们肯定不能填已经填过的数，因此很容易想到的一个处理手段是我们定义一个标记数组vector st;来标记已经填过的数，那么在填第 u个数的时候我们遍历题目给定的 n 个数，如果这个数没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 dfs(nums, u+1);。搜索回溯的时候要撤销该个位置填的数以及标记，并继续尝试其他没被标记过的数。

这里用第一种方法。

vector<vector<int>> res;
vector<int> num;
vector<bool> st;  //标记已经填过的数
//我自己之前的想法是填完一个数删一个数，但是这样没办法把所有的排列都列出来，每个循环只能列一种。
//所有不能删除，应该用一个布尔数组标记已经填过的数。
int n;void dfs(vector<int>& nums, int u){  //u表示格子枚举到哪一位if(u == n){res.push_back(num);return;}for(int i = 0; i < n; i++){if(!st[i]){  //如果该数没被填过st[i] = true;num.push_back(nums[i]);dfs(nums, u+1);num.pop_back();st[i]= false;}}
}
vector<vector<int>> permute(vector<int>& nums) {n = nums.size();st = vector<bool>(n);  //注：st需要初始化，默认为falsedfs(nums, 0);return res;
}

4. 全排列2

在这里插入图片描述
思路：该题与上一道题的区别是序列中有重复数字。
要解决重复问题，我们只要设定一个规则，保证在填第 u个数的时候重复数字只会被填入一次即可。而在本题解中，我们选择对原数组排序，保证相同的数字都相邻，然后每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数字」。

vector<vector<int>> res;
vector<int> num;
vector<bool> st;  //标记已经填过的数
//我自己之前的想法是填完一个数删一个数，但是这样没办法把所有的排列都列出来，每个循环只能列一种。
//所有不能删除，应该用一个布尔数组标记已经填过的数。
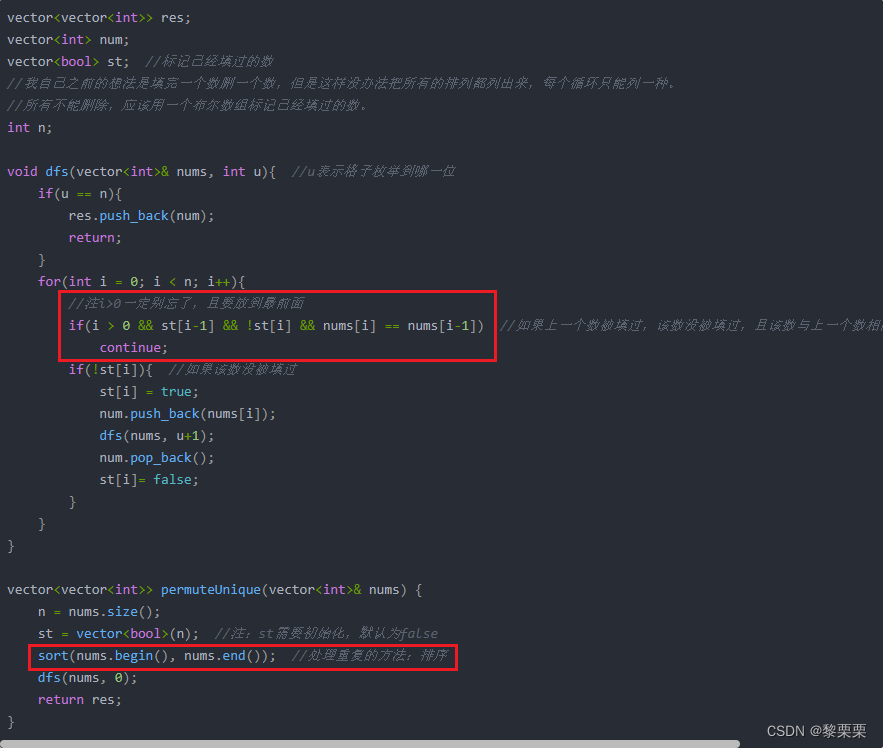
int n;void dfs(vector<int>& nums, int u){  //u表示格子枚举到哪一位if(u == n){res.push_back(num);return;}for(int i = 0; i < n; i++){//注i>0一定别忘了，且要放到最前面if(i > 0 && st[i-1] && !st[i] && nums[i] == nums[i-1])  //如果上一个数被填过，该数没被填过，且该数与上一个数相同，则跳过，不继续枚举。continue;if(!st[i]){  //如果该数没被填过st[i] = true;num.push_back(nums[i]);dfs(nums, u+1);num.pop_back();st[i]= false;}}
}vector<vector<int>> permuteUnique(vector<int>& nums) {n = nums.size();st = vector<bool>(n);  //注：st需要初始化，默认为falsesort(nums.begin(), nums.end());  //处理重复的方法：排序dfs(nums, 0);return res;
}

红框为与上一题的区别。
在这里插入图片描述

5. 子集

在这里插入图片描述
法1：回溯
输入: [1, 2, 3]
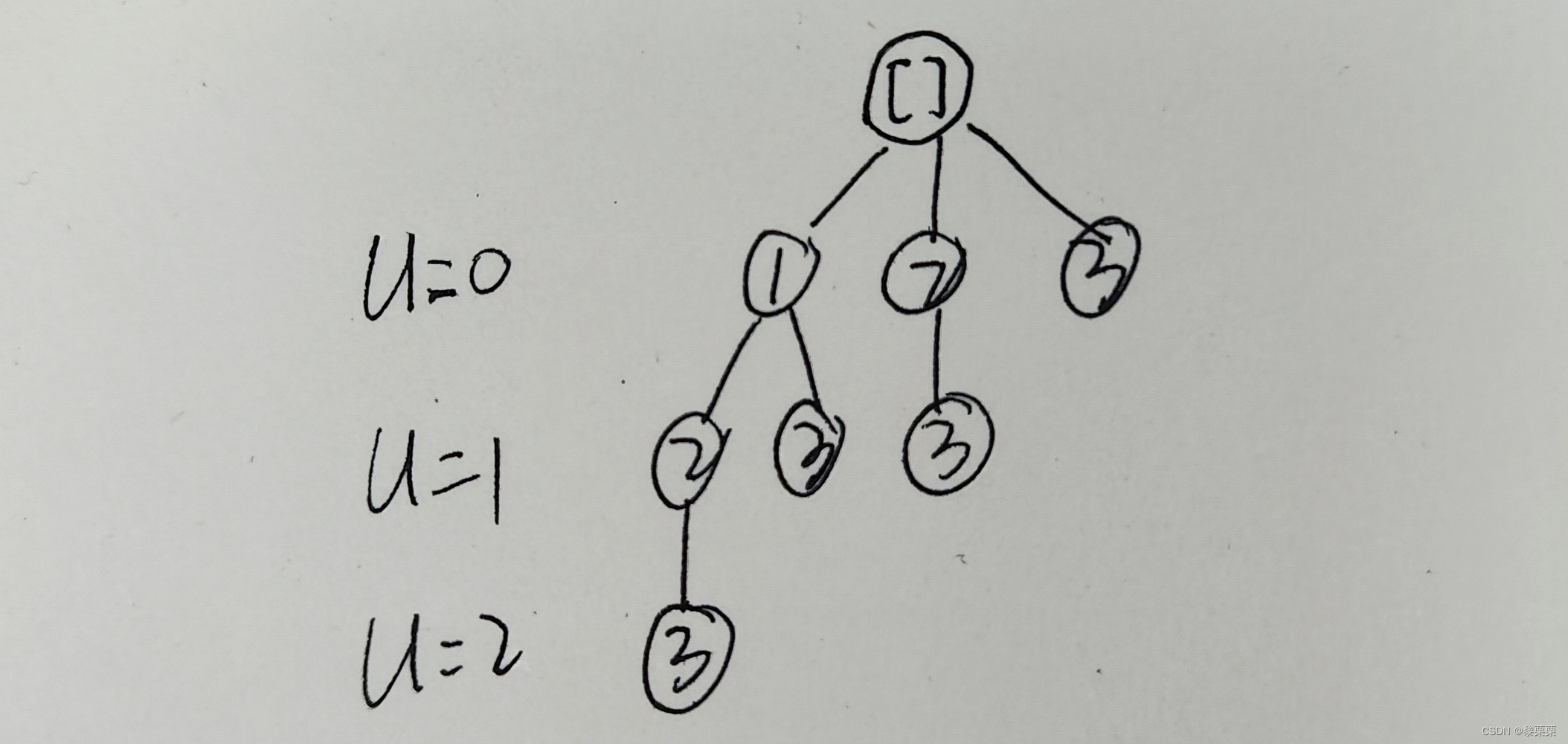
请添加图片描述

//法1：回溯
vector<vector<int>> res = {{}};
vector<int> num;
void dfs(vector<int>& nums, int u){   //u: 从哪一项开始枚举if(u == nums.size())return;for(int i = u; i < nums.size(); i++){num.push_back(nums[i]);res.push_back(num);dfs(nums, i+1);  //注：下一个枚举项是i+1不是u+1num.pop_back();}
}vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return res;
}

法2：循环：利用二进制
这里枚举的所有二进制即为所有子集。
在这里插入图片描述
若i的二进制表示的第j位为1，则将其加入当前子集。
在这里插入图片描述

vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> res;//二进制运算，O(1)的时间复杂度//1<<nums.size()：将1左移n位，结果是一个二进制数，第n位是1，其它位都是0，即2^nfor(int i = 0; i < 1<<nums.size(); i++){  //枚举所有0~2^n-1的二进制vector<int> now;for(int j = 0; j < nums.size(); j++){  //遍历每个二进制//i>>j & 1：将i右移j位，再与1if(i>>j & 1)  //判断i的二进制表示的第j位是否为1now.push_back(nums[j]);}res.push_back(now);}return res;
}

6. 子集2

在这里插入图片描述
思路：
请添加图片描述

vector<vector<int>> res = {{}};
vector<int> num;
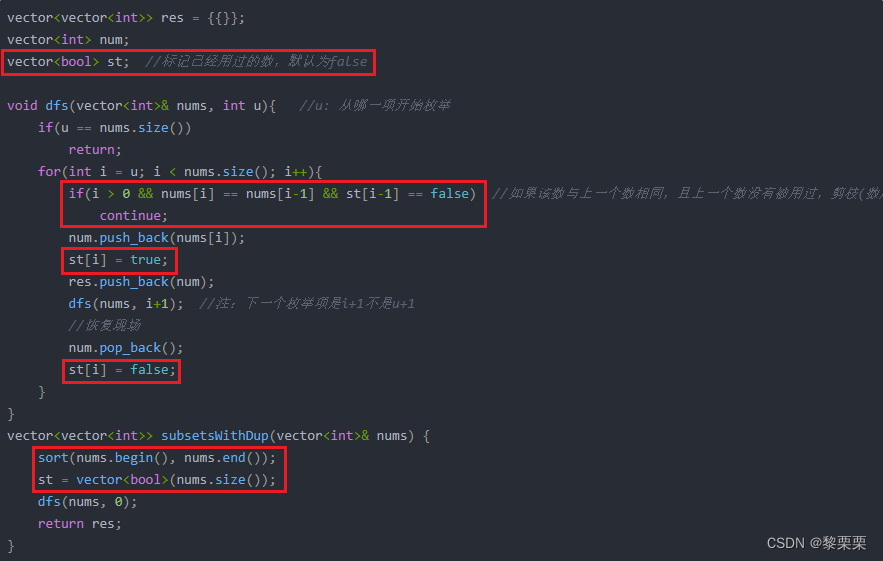
vector<bool> st;  //标记已经用过的数，默认为falsevoid dfs(vector<int>& nums, int u){   //u: 从哪一项开始枚举if(u == nums.size())return;for(int i = u; i < nums.size(); i++){if(i > 0 && nums[i] == nums[i-1] && st[i-1] == false)  //如果该数与上一个数相同，且上一个数没有被用过，剪枝(数层去重)continue;num.push_back(nums[i]);st[i] = true;res.push_back(num);dfs(nums, i+1);  //注：下一个枚举项是i+1不是u+1//恢复现场num.pop_back();st[i] = false;}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());st = vector<bool>(nums.size());dfs(nums, 0);return res;
}

与上一题区别：如下红框部分
在这里插入图片描述

7. 组合总和3

在这里插入图片描述
在这里插入图片描述
思路：
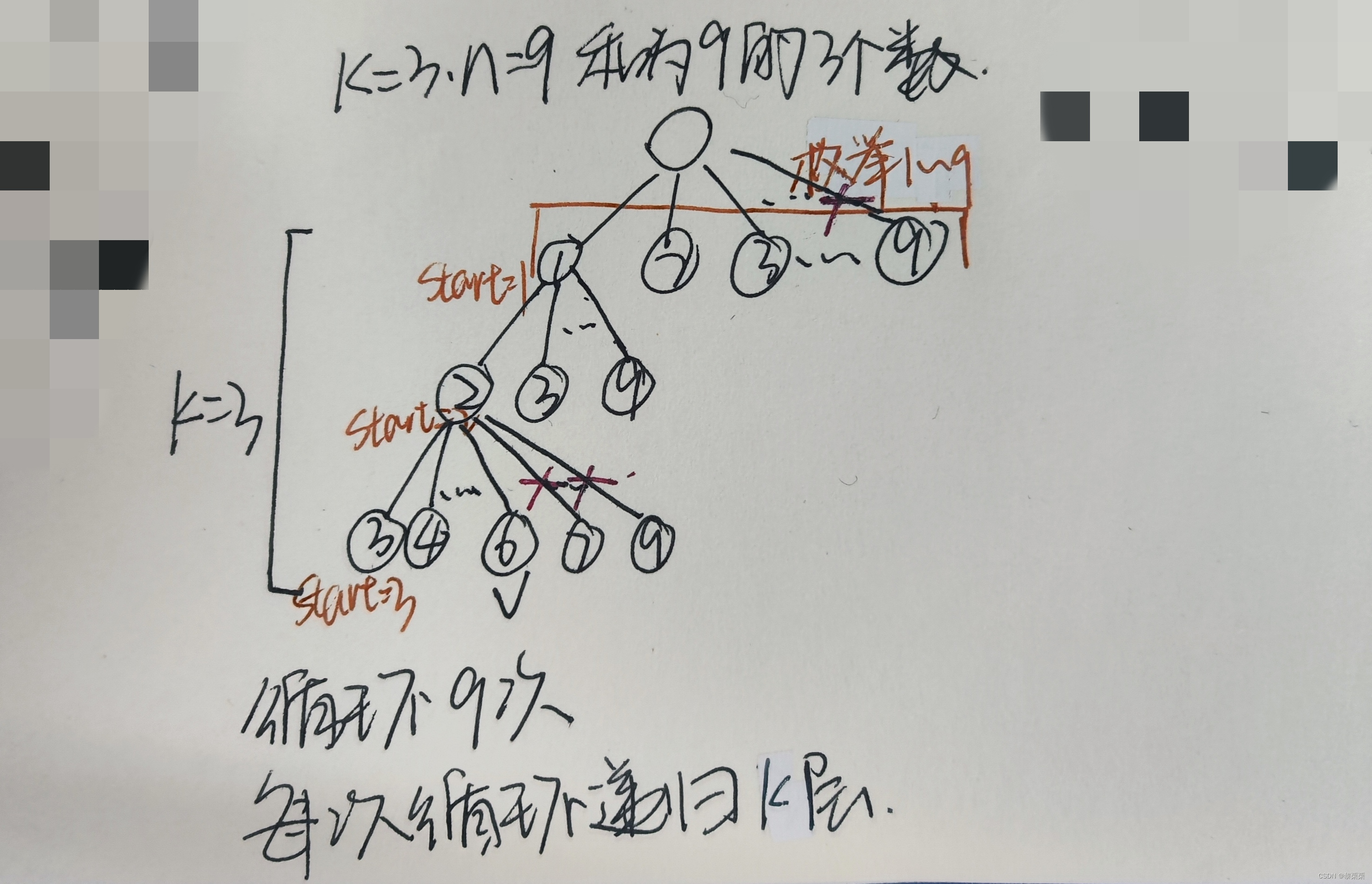
请添加图片描述

小技巧：倒着枚举

vector<int> num;
vector<vector<int>> nums;void dfs(int k, int start, int n){  //枚举到第几个位置，开始枚举的数字，当前选择的数之和if(k == 0){  //如果枚举完了所有位数，则递归结束，返回。if(n == 0)  //如果如果所有数和为n，则将该组合加入答案。nums.push_back(num);//当 n!=0 时直接return：剪枝return;}
//    for(int i = start; i <= 9; i++){
//        num.push_back(i);
//        dfs(k-1, i+1, n-i);  //start保证下一次枚举的数字是当前数字之后的数字
//        num.pop_back();
//    }//这里的for循环可以有一个优化：保证再选k个数，i~9之间一定要留>=k个数才行，所以9-i+1>=k：剪枝for(int i = start; i <= 10-k; i++){num.push_back(i);dfs(k-1, i+1, n-i);  //start保证下一次枚举的数字是当前数字之后的数字num.pop_back();}
}vector<vector<int>> combinationSum3(int k, int n) {dfs(k, 1, n);  //倒着枚举return nums;
}

8. N皇后2

在这里插入图片描述

思路：
全排列：枚举每个位置放哪个数，放这个数的时候不能用前面放过的数（标记已填过的数）
八皇后：枚举每一行皇后放到哪个位置上，放的时候不能产生冲突（标记已填过的列和已填过的斜线）
所以，八皇后问题可以等同于全排列问题。
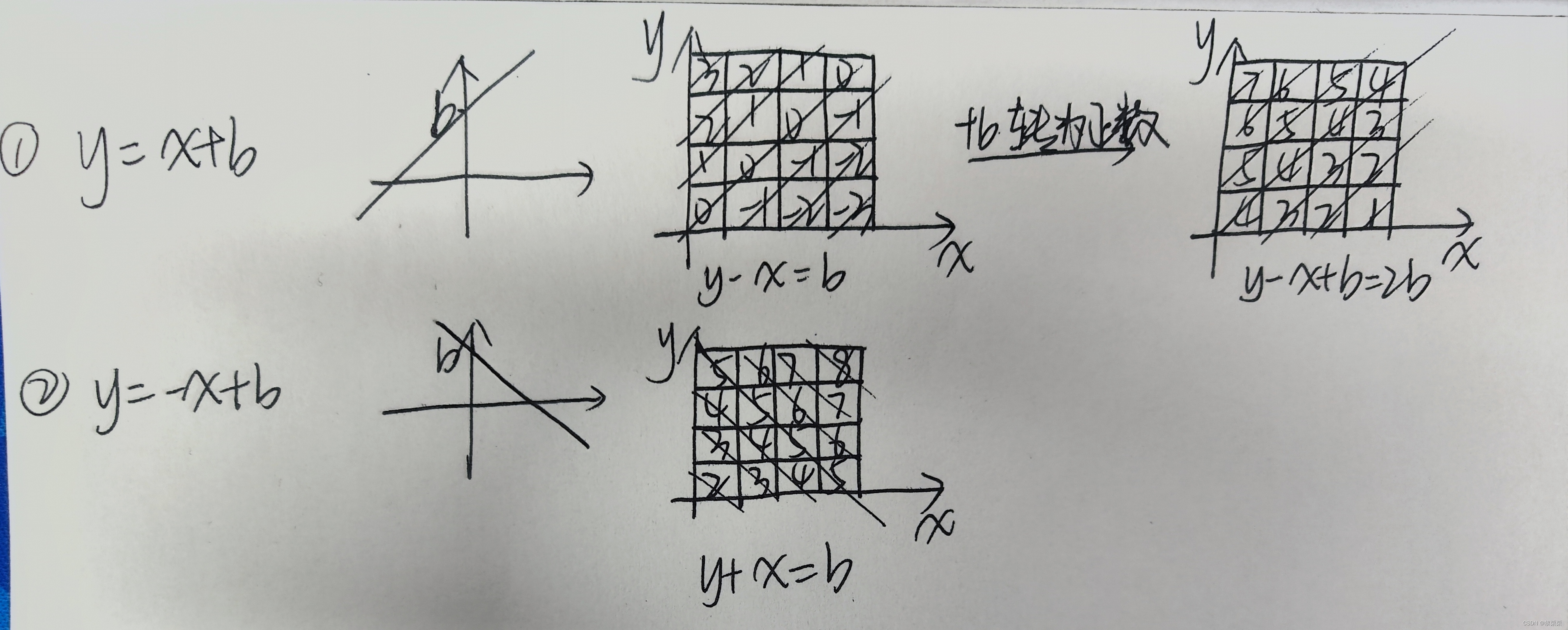
问题：斜线应如何标记？
开两个数组，大小为2n，分别表示正斜线和反斜线。d = ud = vector<bool>(2 * n);
请添加图片描述

int ans = 0;
vector<bool> col, d, ud;  //标记：列，正斜线(y = x + b)，反斜线(y = -x + b)void dfs(int u, int n){  //枚举每一行if(u == n){  //找到一个八皇后解ans++;return;}for(int i = 0; i < n; i++){  //遍历每一列if(!col[i] && !d[u-i+n] && !ud[u+i]){  //如果该列没有皇后，且正斜线和反斜线也没有皇后col[i] = d[u-i+n] = ud[u+i] = true;  //放一个皇后，做标记。dfs(u+1, n);  //递归下一行col[i] = d[u-i+n] = ud[u+i] = false;  //恢复现场}}
}
int totalNQueens(int n) {col = vector<bool>(n);d = ud = vector<bool>(2 * n);dfs(0, n);return ans;
}

9. 解数独

在这里插入图片描述
在这里插入图片描述
本题与八皇后相似，区别是：
搜索所有符合题目要求的路径，返回void；
搜索单条路径，返回bool。

bool row[9][9], col[9][9], cell[3][3][9];  //标记每一行1~9是否已经填了，标记每一列1~9是否已经填了，标记每个小方格1~9是否已经填了。//搜索所有符合题目要求的路径，返回void；搜索单条路径，返回bool。
//注意：这里需要有一个返回值，只要找到一个结果立刻返回，不需要再继续搜索下去了
bool dfs(vector<vector<char>>& board, int x, int y){if(y == 9)  x++, y = 0;  //如果y走到头，下一行重起if(x == 9)  return true;  //如果x走到头，递归结束if(board[x][y] != '.')  //如果该格子有数，则递归下一个return dfs(board, x, y + 1);for(int i = 0; i < 9; i++){  //遍历1~9每一个数//判断该数能否被填if(!row[x][i] && !col[y][i] && !cell[x/3][y/3][i]){//填数，做好标记board[x][y] = i + '1';row[x][i] = col[y][i] = cell[x/3][y/3][i] = true;//递归下一个if(dfs(board, x, y + 1))  return true;//恢复现场board[x][y] = '.';row[x][i] = col[y][i] = cell[x/3][y/3][i] = false;}}return false;
}void solveSudoku(vector<vector<char>>& board) {//遍历一遍棋盘，标记所有已经填过的数for(int i = 0; i < 9; i++){for(int j = 0; j < 9; j++){if(board[i][j] != '.'){int a = board[i][j] - '1';row[i][a] = true, col[j][a] = true, cell[i/3][j/3][a] = true;}}}dfs(board, 0, 0);
}

10. 火柴拼正方形

在这里插入图片描述
在这里插入图片描述
思路：
从大到小枚举所有边。
剪枝：
如果当前木棍拼接失败，且是当前边第一个，则直接剪掉当前分支。
如果当前木棍拼接失败，且是当前边最后一个，则直接剪掉当前分支。
如果当前木棍拼接失败，则跳过接下来所有长度相同的木棍。

vector<bool> st;  //标记每个木棍是否被用过
bool dfs(vector<int>& nums, int u, int cur, int length){  //当前拼到了第几条边，当前边的长度，每条边的长度//注意这两句话顺序不能倒if(cur == length)  u++, cur = 0;  //如果当前边拼好了，开始拼下一条边。if(u == 4)  return true;  //如果所有边都拼好了，返回true//枚举每个木棍for(int i = 0; i < nums.size(); i++){//如果当前木棍没有被用过，且加上当前木棍的长度后不超过每条边的长度，才选择该木棍进行递归。if(!st[i] && cur + nums[i] <= length){st[i] = true;  //标记if(dfs(nums, u, cur + nums[i], length))  return true;  //递归st[i] = false;  //恢复现场//剪枝if(cur == 0)  return false;  //如果当前木棍拼接失败，且是当前边第一个，则直接剪掉当前分支。if(cur + nums[i] == length)  return false;  //如果当前木棍拼接失败，且是当前边最后一个，则直接剪掉当前分支。while(i + 1 < nums.size() && nums[i + 1] == nums[i]) i++;  //如果当前木棍拼接失败，则跳过接下来所有长度相同的木棍。}}return false;
}
bool makesquare(vector<int>& matchsticks) {//异常值判断：若没有木棍或木棍和不能被4整除，返回falseint sum = 0;for(auto u: matchsticks)sum += u;if(sum == 0  || sum % 4 != 0)return false;//初始化stst = vector<bool>(matchsticks.size());//从大到小排序sort(matchsticks.begin(), matchsticks.end());reverse(matchsticks.begin(), matchsticks.end());return dfs(matchsticks, 0, 0, sum/4);
}

这篇关于Leedcode刷题——5 DFS+回溯的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/805418。

相关文章

windos server2022里的DFS配置的实现

windos server2022里的DFS配置的实现

《windosserver2022里的DFS配置的实现》DFS是WindowsServer操作系统提供的一种功能,用于在多台服务器上集中管理共享文件夹和文件的分布式存储解决方案,本文就来介绍一下wi... 目录什么是DFS？优势：应用场景：DFS配置步骤什么是DFS？DFS指的是分布式文件系统（Distr
阅读更多...
hdu 2489 (dfs枚举 + prim)

hdu 2489 (dfs枚举 + prim)

题意： 对于一棵顶点和边都有权值的树，使用下面的等式来计算Ratio 给定一个n 个顶点的完全图及它所有顶点和边的权值，找到一个该图含有m 个顶点的子图，并且让这个子图的Ratio 值在所有m 个顶点的树中最小。 解析： 因为数据量不大，先用dfs枚举搭配出m个子节点，算出点和，然后套个prim算出边和，每次比较大小即可。 dfs没有写好，A的老泪纵横。 错在把index在d
阅读更多...
poj 3050 dfs + set的妙用

poj 3050 dfs + set的妙用

题意: 给一个5x5的矩阵，求由多少个由连续6个元素组成的不一样的字符的个数。 解析： dfs + set去重搞定。 代码： #include <iostream>#include <cstdio>#include <set>#include <cstdlib>#include <algorithm>#include <cstring>#include <cm
阅读更多...
ural 1149. Sinus Dances dfs

ural 1149. Sinus Dances dfs

1149. Sinus Dances Time limit: 1.0 second Memory limit: 64 MB Let  An = sin(1–sin(2+sin(3–sin(4+…sin( n))…) Let  Sn = (…( A 1+ n) A 2+ n–1) A 3+…+2) An+1 For given  N print  SN Input One
阅读更多...
hdu 6198 dfs枚举找规律+矩阵乘法

hdu 6198 dfs枚举找规律+矩阵乘法

number number number Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Problem Description We define a sequence  F : ⋅   F0=0,F1=1 ; ⋅   Fn=Fn
阅读更多...
深度优先（DFS）和广度优先（BFS）——算法

深度优先（DFS）和广度优先（BFS）——算法

深度优先 深度优先搜索算法（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支，当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访
阅读更多...
【每日刷题】Day113

【每日刷题】Day113

【每日刷题】Day113 🥕个人主页：开敲🍉 🔥所属专栏：每日刷题🍍 🌼文章目录🌼 1. 91. 解码方法 - 力扣（LeetCode） 2. LCR 098. 不同路径 - 力扣（LeetCode） 3. 63. 不同路径 II - 力扣（LeetCode） 1. 91. 解码方法 - 力扣（LeetCode） //思路：动态规划。 cl
阅读更多...
回溯——9.全排列

回溯——9.全排列

力扣题目链接 给定一个 没有重复 数字的序列，返回其所有可能的全排列。 示例: 输入: [1,2,3]输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] 解题思路 问题建模：题目要求给出一个数组的所有排列组合，属于典型的全排列问题，这可以用回溯法来解决。回溯法通过递归的方式，依次将数组中的每个元素放入排列中，直到生成
阅读更多...
hot100刷题第1-9题，三个专题哈希，双指针，滑动窗口

hot100刷题第1-9题，三个专题哈希，双指针，滑动窗口

求满足条件的子数组，一般是前缀和、滑动窗口，经常结合哈希表； 区间操作元素，一般是前缀和、差分数组 数组有序，更大概率会用到二分搜索 目前已经掌握一些基本套路，重零刷起leetcode hot 100， 套路题按套路来，非套路题适当参考gpt解法。 一、梦开始的地方， 两数之和 class Solution:#注意要返回的是数组下标def twoSum(self, nums: Lis
阅读更多...
风控系统之指标回溯，历史数据重跑

风控系统之指标回溯，历史数据重跑

个人博客：无奈何杨（wnhyang） 个人语雀：wnhyang 共享语雀：在线知识共享 Github：wnhyang - Overview 回顾 默认你已经看过之前那篇风控系统指标计算/特征提取分析与实现01，Redis、Zset、模版方法。 其中已经介绍了如何利用redis的zset结构完成指标计算，为了方便这篇文章的介绍，还是在正式开始本篇之前回顾一下。 时间窗口 zset
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2