郑州大学2024年3月acm实验室招新赛题解（A-L）

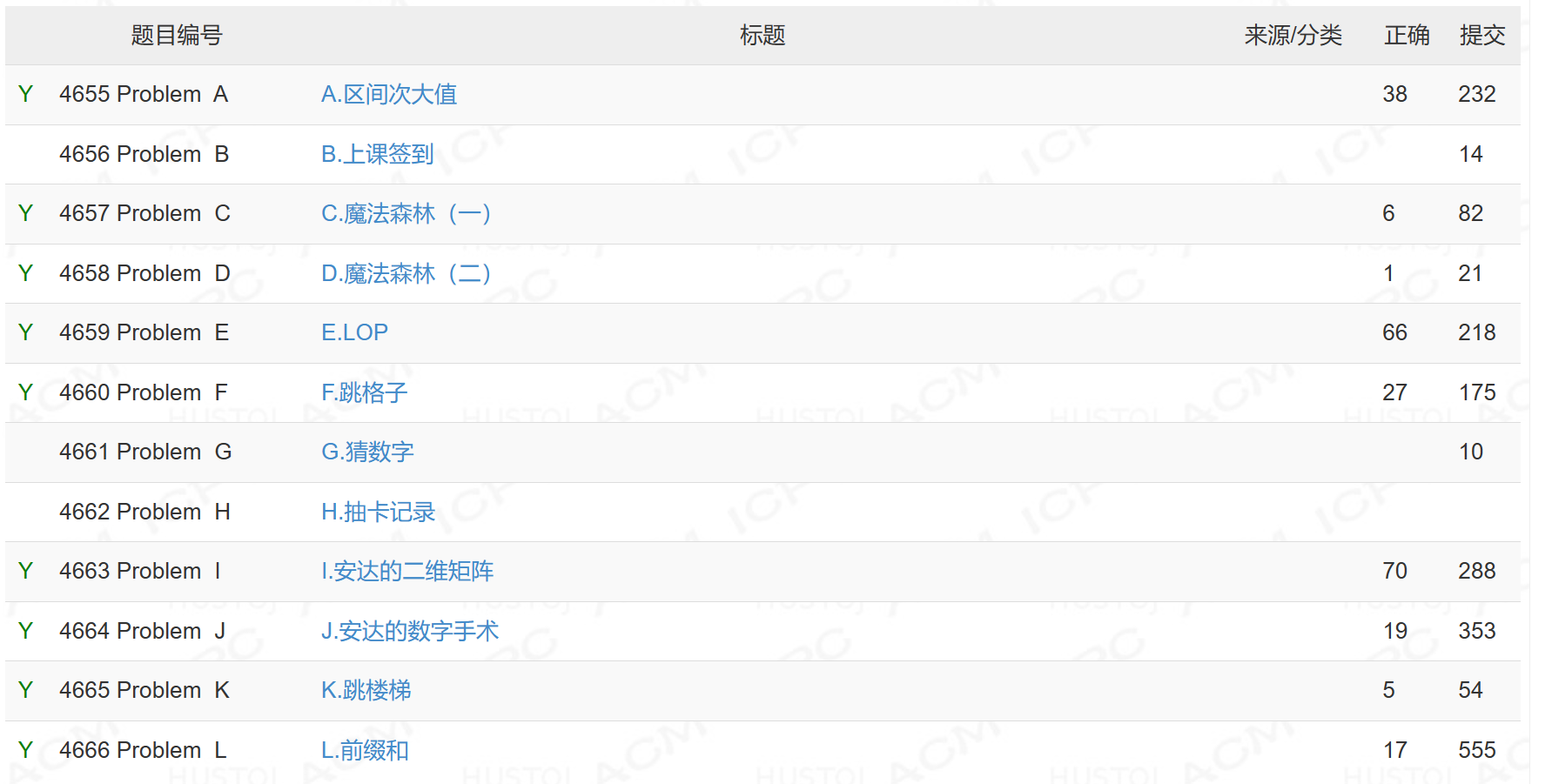
本文主要是介绍郑州大学2024年3月acm实验室招新赛题解（A-L），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这里感谢一下计算机学术交流协会会长，acm实验室的中坚成员，以及本次比赛的出题人之一孙昱涵将他的账号借给了我。

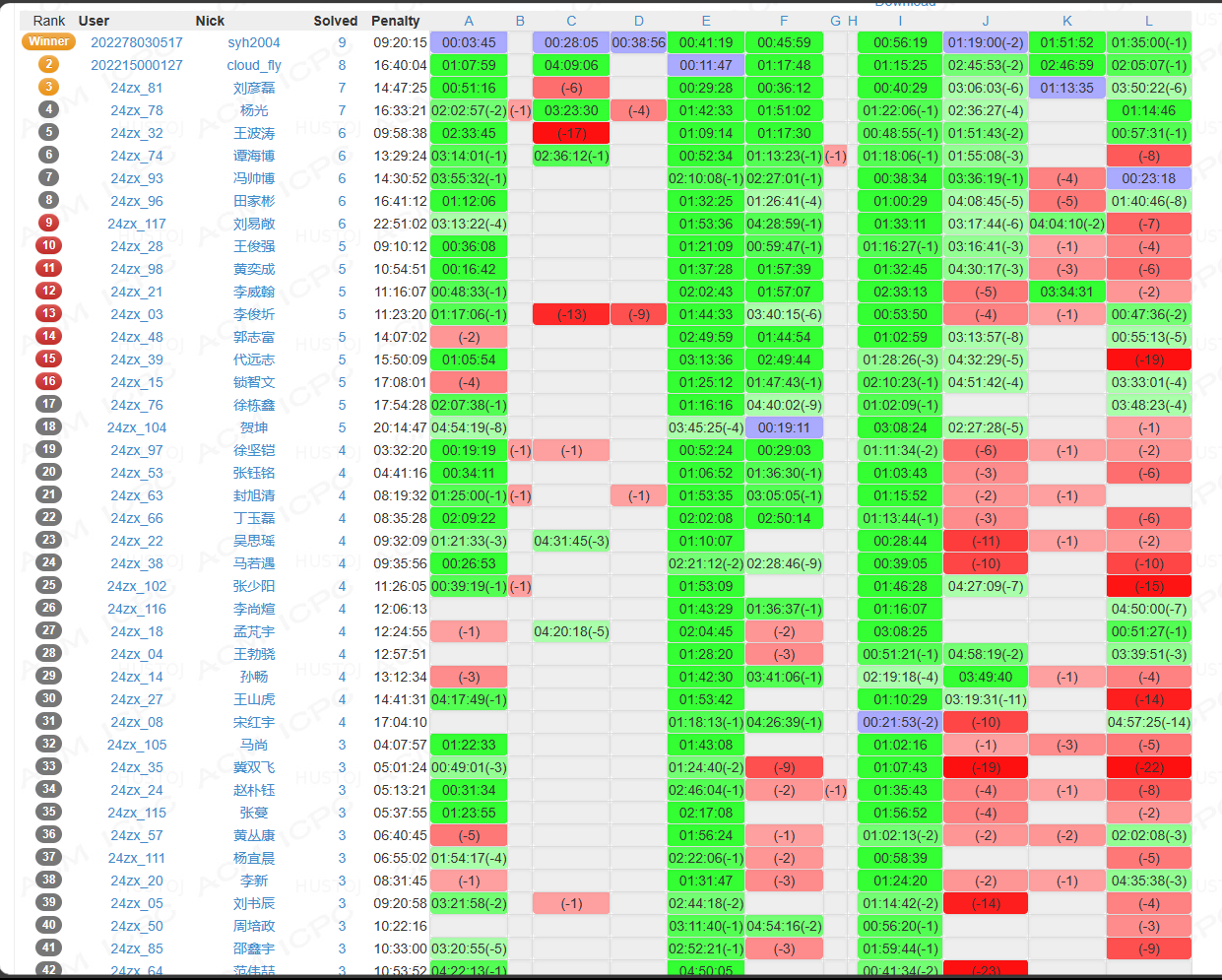
回顾一下的话，这场的难度其实不是很大，不过对招新的新手来说难度还是挺大的。去掉签到都没签出来的选手的话，可以看到大部分选手都只能做出四五题左右（最前面那两个是打星的非正式参赛选手）。

题目难度我觉得按顺序应该是：$A,I,L<C,E,F<D,J,K<B<G,H$ 。

虽然不连校园网大概率连不上，不过姑且还是放一下比赛链接

---

A.区间次大值

题面：

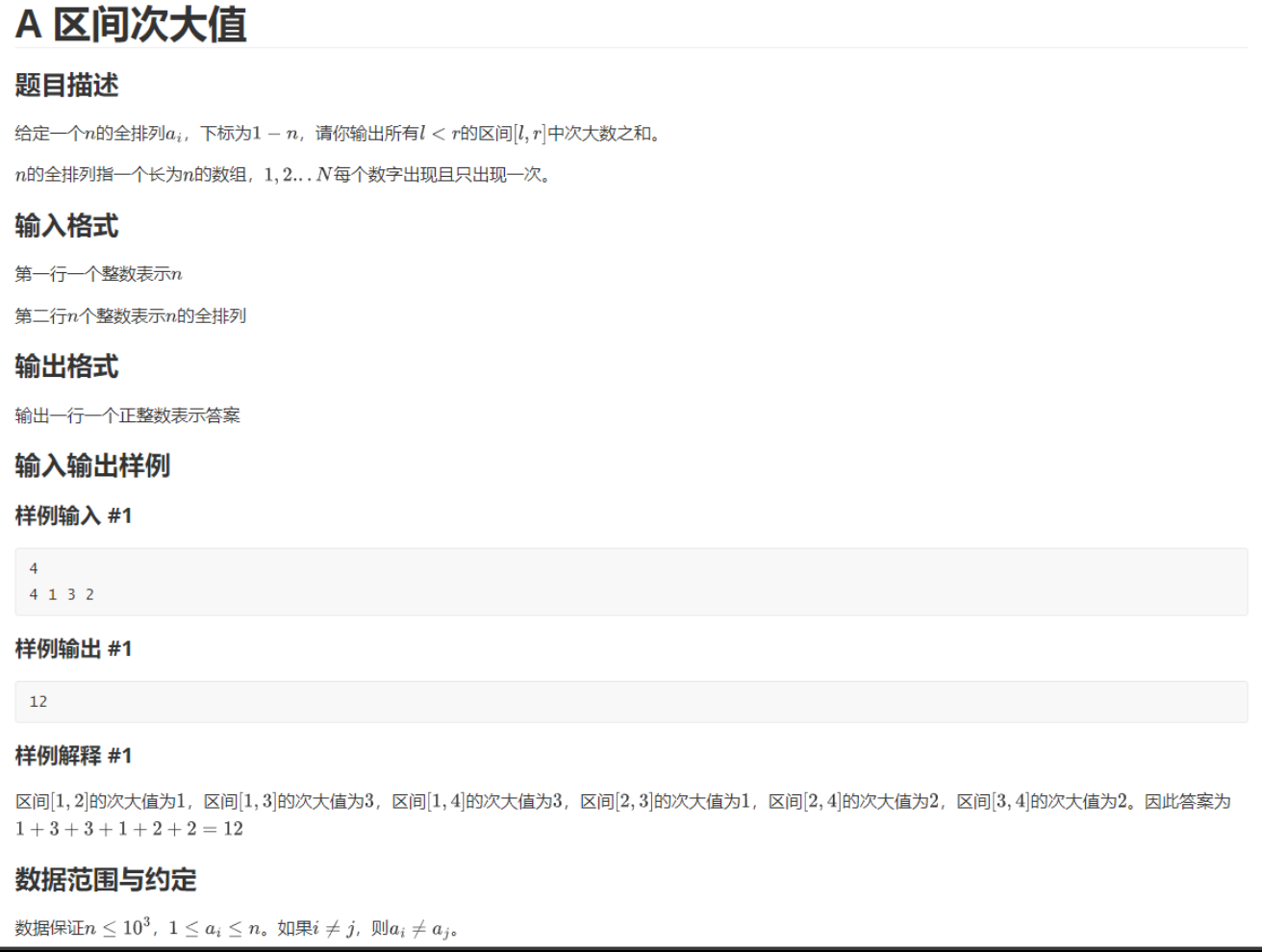
思路：

可以跑 $n^2$，所以直接暴力，枚举左端点 $l$，然后向右移动右端点 $r$，维护住区间的次大值，边移动边统计答案即可。

话说赛时评测机炸了，这题跑出来的全是WA。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e3+5;
typedef long long ll;int n,a[maxn];
ll ans=0;int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int l=1;l<=n;l++){int mx=a[l],mx2=0;for(int r=l+1;r<=n;r++){if(a[r]>mx){mx2=mx;mx=a[r];}else if(a[r]>mx2){mx2=a[r];}ans+=mx2;}}cout<<ans;return 0;
}

---

B.上课签到

题面：

思路：

不考虑统计路径上最大 $a_i$ 的条件的话，就是个普通的最短路。体感上感觉直接去找小于等于 $h$ 的所有路径上的最大 $a_i$ 是不太可能的。但是如果我们验证答案就会很简单，也就是我们提前设定一个最大的 $a_i$ 值，然后跑 $dijkstra$，这样一次验证就是 $(n+m)logn$ 的复杂度。

而这个答案具有单调性，即如果答案是 $x$，那么所有大于 $x$ 的答案也是可以通过验证的。这样就可以二分答案了。总的时间复杂度就是 $(n+m)lo{g}^{2}n$，可以通过。

这个二分既可以是值域上的二分，也可以是对点的 $a_i$ 值排序然后在上面二分。

code：

值域二分：

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#define mk make_pair
using namespace std;
typedef long long ll;
const int maxn=1e4+5;
const int maxm=2e4+5;
const ll inf=1e18;int n,m,st,ed;
ll H,a[maxn];int head[maxn],cnt;
struct edge{int nxt,v;ll w;
}e[maxm<<1];
void add(int u,int v,ll w){e[++cnt].v=v;e[cnt].w=w;e[cnt].nxt=head[u];head[u]=cnt;
}bool dijkstra(ll bound){vector<ll> d(maxn,inf);vector<bool> vis(maxn,false);priority_queue<pair<ll,int>,vector<pair<ll,int> >,greater<pair<ll,int> > > h;d[st]=0;h.push(mk(0ll,st));while(!h.empty()){int u=h.top().second;h.pop();if(u==ed)return true;if(vis[u])continue;else vis[u]=true;for(int i=head[u],v,w;i;i=e[i].nxt){v=e[i].v;w=e[i].w;if(d[u]+w>H || a[v]>bound)continue;if(d[v]>d[u]+w){d[v]=d[u]+w;h.push(mk(d[v],v));}}}return false;
}int main(){cin>>n>>m>>st>>ed>>H;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1,u,v,w;i<=m;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}ll l=a[st],r=1e18,mid;while(l<r){mid=(l+r)>>1;if(dijkstra(mid))r=mid;else l=mid+1;}cout<<((l==1e18)?-1:l)<<endl;return 0;
} 

点集二分：

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <algorithm>
#define mk make_pair
using namespace std;
typedef long long ll;
const int maxn=1e4+5;
const int maxm=2e4+5;
const ll inf=1e9;int n,m,st,ed;
ll H,a[maxn],tmp[maxn];int head[maxn],cnt;
struct edge{int nxt,v,w;
}e[maxm<<1];
void add(int u,int v,int w){e[++cnt].v=v;e[cnt].w=w;e[cnt].nxt=head[u];head[u]=cnt;
}bool dijkstra(ll bound){if(bound<a[st])return false;vector<ll> d(maxn,inf);vector<bool> vis(maxn,false);priority_queue<pair<ll,int>,vector<pair<ll,int> >,greater<pair<ll,int> > > h;d[st]=0;h.push(mk(0ll,st));while(!h.empty()){int u=h.top().second;h.pop();if(u==ed)return true;if(vis[u])continue;else vis[u]=true;for(int i=head[u],v,w;i;i=e[i].nxt){v=e[i].v;w=e[i].w;if(d[u]+w>H || a[v]>bound)continue;if(d[u]+w<d[v]){d[v]=d[u]+w;h.push(mk(d[v],v));}}}return false;
}int main(){cin>>n>>m>>st>>ed>>H;for(int i=1;i<=n;i++)cin>>a[i],tmp[i]=a[i];for(int i=1,u,v,w;i<=m;i++){cin>>u>>v>>w;add(u,v,w);add(v,u,w);}sort(tmp+1,tmp+n+1);if(!dijkstra(tmp[n])){cout<<-1;return 0;}int l=1,r=n,mid;while(l<r){mid=(l+r)>>1;if(dijkstra(tmp[mid]))r=mid;else l=mid+1;}cout<<tmp[l]<<endl;return 0;
} 

---

C.魔法森林（一）

题面：

思路：

跟着操作跑一遍就行了，这题没人写是我没想到的，都被吓住了。

这个题的难点在于传送法阵的强制传送机制。首先需要将两个法阵的位置对应起来，其次需要在移动的时候实现这个传送。

对应法阵位置的方法：因为一个一个字符读取图的时候一定会先遇到一个字母，再遇到一个相同字母。所以存储第一个字母的位置，在读到第二个字母的时候将两个坐标用map相互映射一下就好。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
using namespace std;
const int maxn=5005;int n,m;
string mp[maxn];
map<pair<int,int>,pair<int,int> > sp;
map<char,pair<int,int> > tmp;int fx[]={1,-1,0,0},fy[]={0,0,1,-1};int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>mp[i];mp[i]=" "+mp[i];for(int j=1;j<=m;j++){if(mp[i][j]!='.' && mp[i][j]!='#'){if(tmp.find(mp[i][j])==tmp.end())tmp[mp[i][j]]=make_pair(i,j);else {pair<int,int> a=tmp[mp[i][j]],b=make_pair(i,j);sp[a]=b;sp[b]=a;}}}}int x,y,q;cin>>x>>y>>q;for(;q;q--){char op;cin>>op;int st;switch(op){case 'D':st=0;break;case 'U':st=1;break;case 'R':st=2;break;case 'L':st=3;break;}int vx=x+fx[st],vy=y+fy[st];if(vx<1 || vx>n || vy<1 || vy>m || mp[vx][vy]=='#')continue;if(mp[vx][vy]!='.'){x=sp[make_pair(vx,vy)].first;y=sp[make_pair(vx,vy)].second;}else {x=vx;y=vy;}}cout<<x<<" "<<y<<endl;return 0;
}

---

D.魔法森林（二）

题面：

思路：

一个耿直的BFS，赛时没有写出来的就nm离谱，代码能力不行导致的。

注意一下传送阵是强制传送的。

对传送法阵的处理还是和 $C$ 题一致，难点主要是要想明白在BFS时需要使用 $vis$ 数组对已经经过的位置进行标记，在碰到传送阵时，这个标记是标记传送前的位置还是传送后的位置。

我们 $vis$ 数组的职责是标记已经经过的位置，因为走这个位置之后所有可能的行走路径都会重复。换句话说，我们如果走某个位置之后所有可能的行走路径都会重复，那么就对这个位置进行标记。我们在进入一个位置的传送阵之后，我们还可以从另一个传送阵再传回来，这样有可能到终点更快，而我们如果再走前一个传送阵，后面就会重复，所以我们应该标记的是传送前的法阵位置。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <queue>
#define mk make_pair
using namespace std;
const int maxn=5005;int n,m;
string mp[maxn];
map<pair<int,int>,pair<int,int> > sp;
map<char,pair<int,int> > tmp;
int vis[maxn][maxn];int fx[]={1,-1,0,0},fy[]={0,0,1,-1};int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>mp[i];mp[i]=" "+mp[i];for(int j=1;j<=m;j++){if(mp[i][j]!='.' && mp[i][j]!='#'){if(tmp.find(mp[i][j])==tmp.end())tmp[mp[i][j]]=make_pair(i,j);else {pair<int,int> a=tmp[mp[i][j]],b=make_pair(i,j);sp[a]=b;sp[b]=a;}}}}int sx,sy,ex,ey;queue<pair<int,int> > q;cin>>sx>>sy>>ex>>ey;vis[sx][sy]=1;q.push(mk(sx,sy));while(!q.empty()){int ux=q.front().first,uy=q.front().second;q.pop();if(ux==ex && uy==ey){cout<<vis[ux][uy]-1;return 0;}for(int i=0,x,y;i<4;i++){x=ux+fx[i];y=uy+fy[i];if(x<1 || x>n || y<1 || y>m || mp[x][y]=='#' || vis[x][y])continue;if(mp[x][y]=='.'){vis[x][y]=vis[ux][uy]+1;q.push(mk(x,y));}else {int tx=sp[make_pair(x,y)].first,ty=sp[make_pair(x,y)].second;vis[tx][ty]=vis[ux][uy]+1;q.push(mk(tx,ty));}}}cout<<-1<<endl;return 0;
}

---

E.LOP

题面：

思路：

CF原题，这个题主要是诱导你往游戏规则上想，实际上由于最后一局就是决胜局，因此最后一个赢的就是赢家。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;string s;int main(){cin>>s;cout<<s[s.length()-1];return 0;
}

---

F.跳格子

题面：

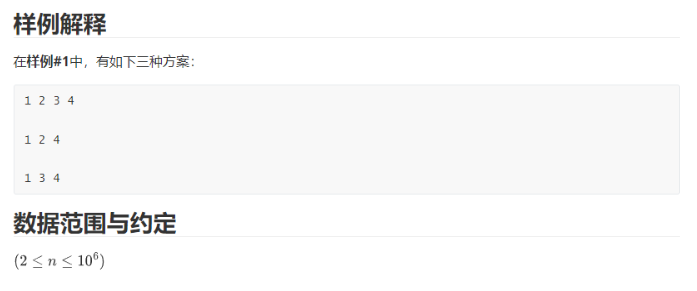
思路：

对某个位置的砖块，它可以由前两个砖块转移过来，因此走到第 $i$ 个位置的砖块的方法数就是到达 $i-1$ 和 $i-2$ 位置上的方法数之和。直接递推即可。

code：

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=1e6+5;int n;
ll dp[maxn];int main(){cin>>n;dp[1]=dp[2]=1;for(int i=3;i<=n;i++){dp[i]=(dp[i-1]+dp[i-2])%mod;}cout<<dp[n];return 0;
}

---

G.猜数字

题面：

思路：

魔王题之一，概率区间dp。

我们在随机取数的时候，除了一发入魂的情况，这个区间都是在一段一段变小的。而转移到某一段子区间的时候，如果我们知道这个子区间的期望，那么我们就可以算出原区间由这个情况转移过来的期望。而子区间也是这样来算每一种情况贡献的期望。

那么思路就比较明显了，设 $dp[i][j]$ 为区间 $[i,j]$ 生成 $x$ 的期望。发现下次生成的数只有三种情况：

1. 正好生成 $x$，这时期望贡献就是 $\frac{1}{j-i+1}$。
2. 生成的数为 $k(i\le k<x)$ 时，这时候期望为 $\frac{1}{j-i+1}\ast (dp[k][j]+1)$
3. 生成的数为 $k(x<k\le j)$ 时，这时候期望为 $\frac{1}{j-i+1}\ast (dp[i][k]+1)$

那么总的期望为： $$\begin{gathered} dp[i][j]=\frac{1}{j-i+1}+\sum _{k=i+1}^{x-1}\frac{1}{j-i+1}\ast (dp[k][j]+1)+ \\ \sum _{k=x+1}^{j-1}\frac{1}{j-i+1}\ast (dp[i][k]+1) \end{gathered}$$$$=\frac{1}{j-i+1}\ast (1+\sum _{k=i+1}^{x-1}(dp[k][j]+1)+\sum _{k=x+1}^{j-1}(dp[i][k]+1))$$

这里没有把求和符号中的 $+1$ 那个部分单独拆出来，是因为 $i+1$ 与 $x-1$ 以及 $x+1$ 与 $j-1$ 的大小关系不明确，有可能 $i+1<x-1$ 也有可能 $i+1>x-1$，直接拆出来不知道有几个 $1$。

回到正题，这个式子我们正常算的时候需要枚举左右端点和枚举 $k$，是 $O(n^3)$ 的，但是题目要求是 $O(n^2)$，的那么如何优化这个式子呢，如果我们把 $dp[k][j]+1$ 这个部分看成一个整体，发现当 $j$ 固定的时候，它相当于一个前缀和。同理当 $i$ 固定的时候，$dp[i][k]+1$ 也相当于一个前缀和。

那么怎么边算边记录这个前缀和呢？假设我们第一维枚举 $i$，第二维枚举 $j$，那么我们第二维在枚举 $j$ 的时候，$i$ 就是固定的，用一个变量记录 $s_{ik}={\sum }_{k=x+1}^{j-1}(dp[i][k]+1)$ 即可。而 ${\sum }_{k=i+1}^{x-1}(dp[k][j]+1)$ 这个前缀和看似不好处理，实际上我们对每个 $j$ 单独开一个变量来记录就可以了，具体来说就是用 $s_{kj}[j]={\sum }_{k=i+1}^{x-1}(dp[k][j]+1)$。

这题我一开始其实是从区间 $[1,n]$ 为起点开始推的，但是从 $[i,j]\to [1,n]$ 的期望和 $[i,j]\to x$ 的期望不是一回事，两者不能直接互通，导致想法假了，赛时被单防。不能给新生一点小小的acm震撼真是太可惜了。

code：

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=5005;
const ll mod=998244353;ll qpow(ll a,ll b){b%=mod-1;ll base=a%mod,ans=1;while(b){if(b&1){ans*=base;ans%=mod;}base*=base;base%=mod;b>>=1;}return ans;
}
ll inv(ll x){return qpow(x,mod-2);}int n,x;
ll f[maxn][maxn];
ll skj[maxn],sik;int main(){cin>>n>>x;for(int i=x;i>=1;i--){sik=0;for(int j=x;j<=n;j++){f[i][j]=(1ll+skj[j]+sik)*inv(j-i+1)%mod;skj[j]=(skj[j]+f[i][j]+1)%mod;sik=(sik+f[i][j]+1)%mod;}}cout<<f[1][n]<<endl;return 0;
}

---

H.抽卡记录

题面：

思路：

魔王题之一。

如果去除掉变化至多 $k$ 次的限制条件，这个题就是个裸的 $LIS$ （最长上升子序列）问题。加上 $k$ 次的限制条件就在原来的基础上多加一维其实就可以了，要界定最后是上升段还是下降段，就再加一维，这本质还是 $LIS$ 问题。经验还是不足。

具体来说，设 $dp[i][j][0/1]$ 表示前 $i$ 个数以第 $i$ 个数结尾（也就是必选第 $i$ 个数），变化了 $j$ 次，最后一段是在上升段还是下降段的最少删除次数。

转移的话就是枚举 $1\sim i-1$ 尝试由前面的某个位置转移过来。转移方法看代码。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1005;
const int maxk=15;
const int inf=1e9;int n,m,a[maxn];
//前i个数，变化k次，现在向上/下变化的最小删除次数 
int dp[maxn][maxk][2];int main(){cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int i=0;i<=n;i++)for(int j=0;j<=m;j++)for(int k=0;k<=1;k++)dp[i][j][k]=inf;for(int i=1;i<=n;i++){dp[i][0][0]=dp[i][0][1]=i-1;for(int j=i-1;j>=1;j--){for(int k=0;k<=m;k++){if(a[i]>a[j]){dp[i][k][0]=min(dp[i][k][0],dp[j][k][0]+i-j-1);if(k>0)dp[i][k][0]=min(dp[i][k][0],dp[j][k-1][1]+i-j-1);}else if(a[i]<a[j]){dp[i][k][1]=min(dp[i][k][1],dp[j][k][1]+i-j-1);if(k>0)dp[i][k][1]=min(dp[i][k][1],dp[j][k-1][0]+i-j-1);}else continue;}}}int ans=n-1;for(int i=1;i<=n;i++)for(int k=0;k<=m;k++)ans=min(ans,min(dp[i][k][0],dp[i][k][1])+n-i);cout<<n-ans;return 0;
}

---

I.安达的二维矩阵

题面：

思路：

签到题。读入第 $i$ 行的时候顺便数一下当前行有多少个 $1$，另外设置两个变量分别记录之前 $1$ 最多的行的编号和 $1$ 的个数，如果第 $i$ 行的 $1$ 个数更多，就转而记录第 $i$ 行的信息。

code：

#include <iostream>
#include <cstdio>
using namespace std;int n,m;int main(){cin>>n>>m;int x=1,y=0;for(int i=1,t;i<=n;i++){int cnt=0;for(int j=1;j<=m;j++){cin>>t;if(t==1)cnt++;}if(cnt>y)x=i,y=cnt;}cout<<x<<" "<<y;return 0;
}

---

J.安达的数字手术

题面：

思路：

如果是正常的删除某一个数位上的数，这个数的数位会减少 $1$，但是如果删除第一位的时候能出现前导零，就可以删掉多位数，因此如果删第一位能出现前导零，从而删掉多位，就删第一位就行了。

但是如果不是这种情况，考虑如何删数能使得数字最小（数位相同时其实就是字典序最小），发现其实我们删数的时候就是把第 $i$ 位的数删掉，然后把第 $i+1$ 位的数放到第 $i$ 位上，后面依次向前补。因此我们删数的时候一定删那种第 $i$ 位上的数大于第 $i+1$ 位上的数，这样后面数位向前补的时候，第 $i$ 位才会变得更小。因为是字典序最小，只要高位更小，整个串就最小。因此我们贪心地找到第一个 第 $i$ 位上的数大于第 $i+1$ 位上的数 的位置，删掉它就行了。找到最后都没找到的话，就删掉最后一位。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;int n;
string s;bool lt(string a,string b){if(a.size()!=b.size())return a.size()<b.size();else return a<b;
}int main(){cin>>n>>s;if(n==1){cout<<0<<endl;return 0;}string t,t2;int idx=1;while(idx<n && s[idx]=='0')idx++;t=s.substr(idx);if(!t.size())t="0";for(int i=1;i<n;i++){if(i+1<n && s[i]>s[i+1]){t2=s.substr(0,i)+s.substr(i+1);break;}}if(!t2.size())t2=s.substr(0,n-1);if(lt(t,t2))cout<<t;else cout<<t2;return 0;
}

---

K.跳楼梯

题面：

思路：

一开始我也往 $BFS$ 上想了，但是发现太过复杂，有可能需要访问负的下标，正的下标也可能超过 $n$。翻一下榜，发现 $A$ 掉这题的人有过的很快的，这说明这个题的码量和书写的难度并不大，所以直接尝试推结论，几分钟就出了。

这个题其实就相当于是选取等差数列上的某几个数改成 $-1$，使得它们的和等于 $n$。首先罗飞云要到达第 $n$ 层，首先你等差数列的总和必须得不小于 $n$，这样你把某些数改成 $-1$ 的时候，总和会变小，它才有可能等于 $n$。

发现正因为是等差数列，它有一个很优美的性质，就是我们只选择一个数变成 $-1$ 的话，从 $1$ 到 $x$总和会在原来的基础上减少 $2,3,4,\dots ,x+1$。如果我们找到第一个 $x$ ，使得 $1\sim x$ 的和 $tot$ 大于等于 $n$，这时只要 $tot$ 和 $n$ 相差不为 $1$，我们就可以从 $1\sim x$ 找到一个数把总和减少到 $n$。

这是因为 $tot-x$ 相当于 $1\sim x-1$ 的和，根据我们上面 $x$ 是第一个 使得 $1\sim x$ 的和 $tot$ 大于等于 $n$ 的位置 的前提，也就是 $tot-n<x$ ，如果 $tot-n\ge 2$ ，我们就一定能找到这个差值，继而找到变成 $-1$ 的那个数，这时答案就是 $x$。而当 $tot=n$ 的时候，答案就是 $x$，当 $tot-n=1$ 时，必须额外补一个 $-1$，这时答案就是 $x+1$。

这个 $x$ 的计算可以二分来算。直接暴力枚举 $O(t\sqrt{n})$ 也不会超时。

code：

#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
const int maxn=1e6+5;int T,n;int main(){cin>>T;while(T--){cin>>n;int l=1,r=2000,mid;while(l<r){mid=(l+r)>>1;if(mid*(mid+1)/2>=n)r=mid;else l=mid+1;}if(l*(l+1)/2-n==1)cout<<l+1<<endl;else cout<<l<<endl;}return 0;
}

---

L.前缀和

题面：

思路：

就是算前缀和然后二分查询，题面问的很直白了。不过这题卡cin，需要取消同步或者改用scanf。

code：

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;int n,Q;
ll s[maxn],sum;int main(){ios::sync_with_stdio(false);cin.tie(0); cin>>n>>Q;for(int i=1;i<=n;i++){cin>>s[i];s[i]+=s[i-1];}while(Q--){cin>>sum;if(sum>s[n])cout<<-1<<"\n";else cout<<(lower_bound(s+1,s+n+1,sum)-s)<<"\n";}return 0;
}

这篇关于郑州大学2024年3月acm实验室招新赛题解（A-L）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---