本文主要是介绍青蛙的约会 (exgcd 扩展gcd),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
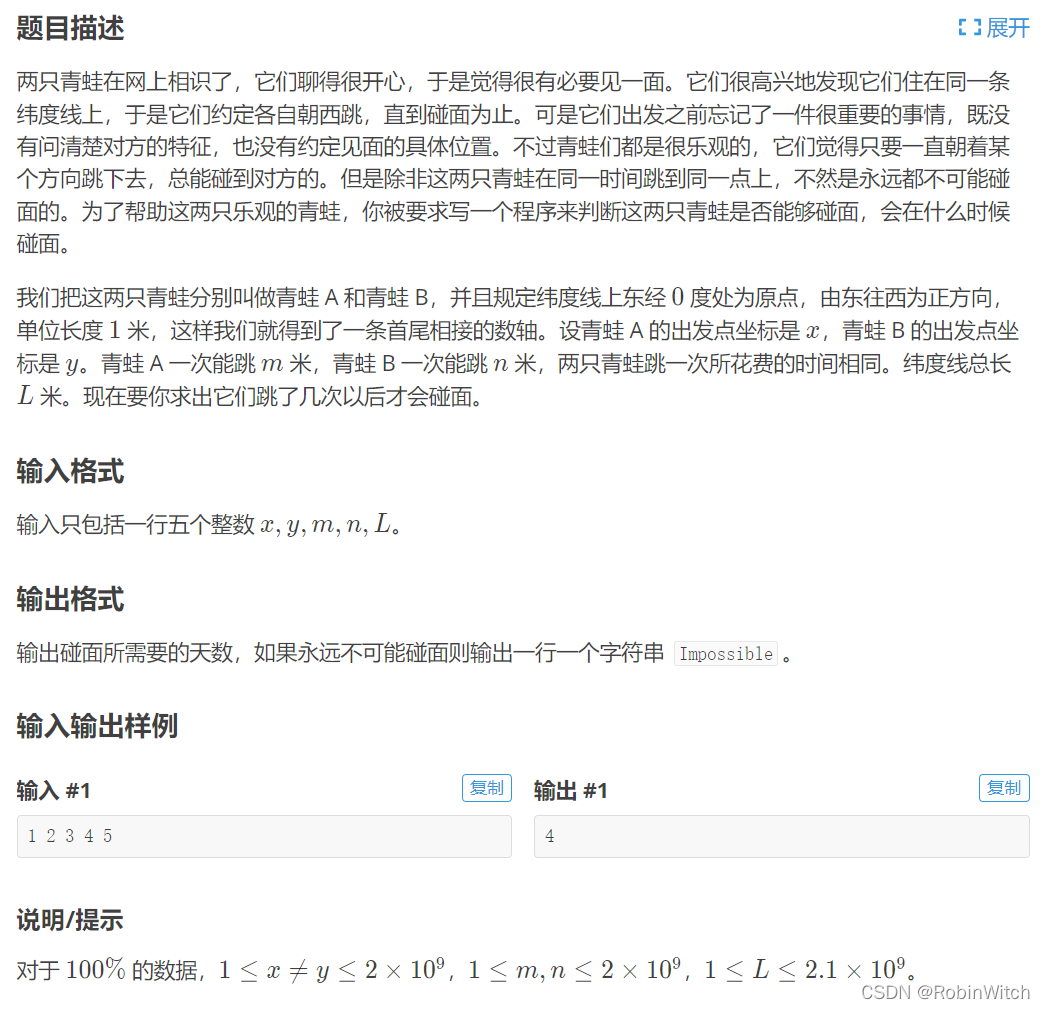
题目链接 青蛙的约会
这里可以推荐大家看看题解中的第一篇皎月半洒花大佬的题解
下面是我自己的一个小思路,写完后写代码就可以说不是一般轻松了,

再附上关于对最后一步负数如何转正数的一个理解,比如S/gcd和l/gcd来源的一个视角的解答,这本书挺好的,安利给大家!《数论概论》【美】约瑟夫 H.西尔弗曼写的

附上代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long //最后的一个问题还是这个long long 的问题...int果然有毒
ll exgcd(ll a, ll b, ll& x, ll& y) { //扩展欧几里得算法,根据对于任意整数a,b必存在x与y使得ax+by=gcd(a,b)有解,该函数能够返回a与b的最大公因数,if (!b) { //以及可以得到上述x与y的值x = 1;y = 0;return a;}ll tx, ty;ll res = exgcd(b, a % b, tx, ty);x = ty;y = tx - a / b * ty;return res;
}
int main()
{ll x, y, m, n, l;cin >> x >> y >> m >> n >> l;ll s = x - y;ll w = n - m;if (w < 0)//考虑到负数情况{w = -w;s = -s;}ll k, z;ll gcd=exgcd(w, l, k, z);if (s % gcd != 0){cout << "Impossible" << endl;return 0;}ll res = (k * s / gcd % (l / gcd) + (l / gcd)) % (l / gcd);cout << res;
}
这篇关于青蛙的约会 (exgcd 扩展gcd)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



