本文主要是介绍【CODEFORCES】 C. Number of Ways，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
You've got array a[1], a[2], ..., a[n], consisting of n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.
More formally, you need to find the number of such pairs of indices i, j (2 ≤ i ≤ j ≤ n - 1), that 
.
The first line contains integer n (1 ≤ n ≤ 5·105), showing how many numbers are in the array. The second line contains n integers a[1],a[2], ..., a[n] (|a[i]| ≤ 109) — the elements of array a.
Print a single integer — the number of ways to split the array into three parts with the same sum.
5 1 2 3 0 3
2
4 0 1 -1 0
1
2 4 1
0
题解：此题并不算难，我们设lsum[i]是从1到i所有数组元素的和（前缀和），rsum[i]是从i到n所有数组元素的和，那么现在就是要找到一组i,j，i<j，j-i>=2，lsum[i]=lsum[j]=sum/3。看到题目数据较大，n方算法不划算，所以用一个c数组记录，c[i]表示i之后有多少个rsum[i]与sum/3相等，这样就把时间复杂度降为O（n）了。
感觉主要是前缀和...
#include <iostream>
#include <cstdio>using namespace std;int a[500003],c[500003],n;
long long lsum[500003],rsum[500003],sum,ans;
int main()
{scanf("%d",&n);for (int i=1;i<=n;i++){scanf("%d",&a[i]);sum+=a[i];lsum[i]=a[i]+lsum[i-1];}if (sum%3!=0){cout <<0<<endl;return 0;}for (int i=1;i<=n;i++) rsum[i]=sum-lsum[i]+a[i];for (int i=n;i>=1;i--) if (rsum[i]==sum/3) c[i]=c[i+1]+1;else c[i]=c[i+1];for (int i=1;i<=n-1;i++) if (lsum[i]==sum/3) ans+=c[i+2];cout <<ans<<endl;return 0;
}
这篇关于【CODEFORCES】 C. Number of Ways的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
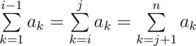