打表技巧：N个苹果，用6号袋和8号袋装，必须装满每个袋子，最少需要多少个袋子才能装满

打表技巧：N个苹果，用6号袋和8号袋装，必须装满每个袋子，最少需要多少个袋子才能装满？

提示：有些题目，结果只与一维变量n有关，可以暴力解，打印一批结果，
然后观察结果可能存在的与i之间的特定规律，直接打表，用的时候查表就行，速度o(1)

文章目录

• 打表技巧：N个苹果，用6号袋和8号袋装，必须装满每个袋子，最少需要多少个袋子才能装满？
• • @[TOC](文章目录)
• 题目
• 一、审题
• 先暴力解：贪心
• 再观察是否能打表？
• 总结

题目

N个苹果，用6号袋和8号袋装，分别能装6个和8个苹果
必须装满每个袋子，最少需要多少个袋子才能装满？
无法满足要求的话，返回-1；

一、审题

示例：
N=7
6号装6个，剩下1个，没法装！返回-1
N=8
8号就能一次性装下
N=12，至少2个6号袋子

先暴力解：贪心

N个苹果，咱们直觉是，拿大号袋子，装，尽可能1个袋子，装更多的苹果，这样袋子数量少
但是呢？
就像N=12一样，你先装8号，还剩4个，找不到袋子装
只能考虑8号袋子来0个，所以剩下的12个用6号袋子装，至少2个
如果N=7这种，8和6依次都没法装，不好意思，那就返回-1

不妨设需要k8个8号袋子，k6个6号袋子，自然先装8号袋子
（1）默认最开始k8=k6=-1，暂时都不符合条件
（2）先装8号袋子：k8=N/8
（3）那还余下M=N-8*k8个苹果，剩下的只能用6号袋子来装，那如果M%6=0就可以装，直接返回k6+k8；否则需要尝试新的k8
（4）如果（3）没法装的话（即M%6!=0），则让k8–，即8号袋子少拿一个，然后回（3）
（5）如果直到k8=0了，k6仍然没法装，那不好意思，整体就装不下了。

举个例子
N=100
（1）默认最开始k8=k6=-1，暂时都不符合条件
（2）先装8号袋子：k8=N/8=100/8=12，
（3）那还余下M=N-8*k8 = 100-12×8=100-96=4个苹果，剩下的只能用6号袋子来装，那如果M%6=0就可以装，直接返回k6+k8；否则需要尝试新的k8
（4）如果（3）没法装的话（即M%6=4%6=4!=0），则让k8–，即8号袋子少拿一个，k8=11,然后回（3）

（3）那还余下M=N-8*k8 = 100-11×8=100-88=12个苹果，剩下的只能用6号袋子来装，那如果M%6=12%6=0就可以装，直接返回k6+k8；即2+11个袋子=13个。

明白了这意思吧？
先尽量拿大号袋子装，然后还有剩余就让小号装，能装下，OK，两者和就是最少的袋子
否则就得让大号袋子少装一袋，再看看小号袋子能否装下，能就是两者的和
一直到大号1个都不用！用小号袋子看看能装完么？能就是小号袋的数量，不能则不好意思了！返回-1，压根没法装

手撕代码看看打印出来的结果如何？

    //复习：//先尽量拿大号袋子装，然后还有剩余就让小号装，能装下，OK，两者和就是最少的袋子//否则就得让大号袋子少装一袋，再看看小号袋子能否装下，能就是两者的和//一直到大号1个都不用！用小号袋子看看能装完么？能就是小号袋的数量，不能则不好意思了！返回-1，压根没法装public static int leastDaiZi(int n){if (n <= 5) return -1;//6之下，不行//不妨设需要k8个8号袋子，k6个6号袋子，自然先装8号袋子int k8 = -1;int k6 = -1;//（1）默认最开始k8=k6=-1，暂时都不符合条件//（2）先装8号袋子：k8=N/8k8 = n / 8;int m = n - k8 * 8;//剩下的苹果数while (m >= 0 && k8 >= 0){//8号袋子不能为-//（3）那还余下**M**=N-8*k8个苹果，剩下的只能用6号袋子来装，// 那如果M%6=0就可以装，直接返回k6+k8；否则需要尝试新的k8if (m % 6 == 0){k6 = m / 6;break;//结束k6!=-1}else {//（4）如果（3）没法装的话（即M%6!=0），则让k8--，即8号袋子少拿一个，然后回（3）k8--;m = n - k8 * 8;//剩下的苹果数}}//（5）如果直到k8=0了，k6仍然没法装，那不好意思，整体就装不下了。return k6 != -1 ? k8 + k6 : -1;}public static void test(){for (int i = 1; i <=100 ; i++) {
//            System.out.print(i +":"+ minBag(i));
//            System.out.println();System.out.print(i +":"+ leastDaiZi(i));System.out.println();//打印出前100看看}}

1:-1
2:-1
3:-1
4:-1
5:-1
6:1
7:-1
8:1
9:-1
10:-1
11:-1
12:2
13:-1
14:2
15:-1
16:2
17:-1
18:3
19:-1
20:3
21:-1
22:3
23:-1
24:3
25:-1
26:4
27:-1
28:4
29:-1
30:4
31:-1
32:4
33:-1
34:5
35:-1
36:5
37:-1
38:5
39:-1
40:5
41:-1
42:6
43:-1
44:6
45:-1
46:6
47:-1
48:6
49:-1
50:7
51:-1
52:7
53:-1
54:7
55:-1
56:7
57:-1
58:8
59:-1
60:8
61:-1
62:8
63:-1
64:8
65:-1
66:9
67:-1
68:9
69:-1
70:9
71:-1
72:9
73:-1
74:10
75:-1
76:10
77:-1
78:10
79:-1
80:10
81:-1
82:11
83:-1
84:11
85:-1
86:11
87:-1
88:11
89:-1
90:12
91:-1
92:12
93:-1
94:12
95:-1
96:12
97:-1
98:13
99:-1
100:13

再观察是否能打表？

有这么几个规律：
n<=17之前

1:-1
2:-1
3:-1
4:-1
5:-1
6:1
7:-1
8:1
9:-1
10:-1
11:-1
12:2
13:-1
14:2
15:-1
16:2
17:-1

n取6和8，ans=1
n取12,14和16，ans=2
其余全部ans=-1

n取18开始逢奇数n全-1

逢偶数n，ans会分组以4个相同的数字递增出现
类似这样：3 3 3 3
4 4 4 4
5 5 5 5
……

18:3
19:-1
20:3
21:-1
22:3
23:-1
24:3
25:-1
26:4
27:-1
28:4
29:-1
30:4
31:-1
32:4
33:-1
34:5
35:-1
36:5
37:-1
38:5
39:-1
40:5

能看懂吧？
因为是4个数字，和4个-1一组，共8个数
咱们把18挪到0位置算的话
起点就是n-18

每一次ans是多少呢？(n-18) / 8 + 3

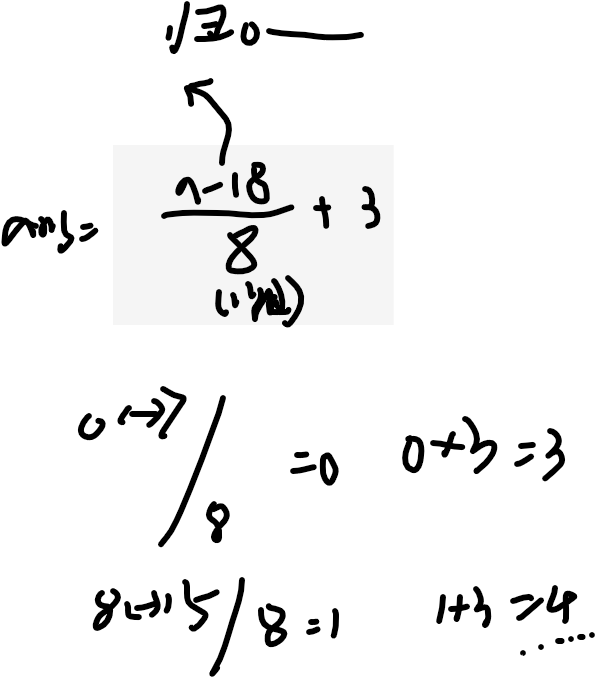
8个数一批，从0 1 2 3叠加到3上，就是数字递增的规律
比如18 20 22 24
他们-18再÷8，都是0,0+3，就是3，四个3
从26开始 28 30 32，他们-18再÷8，都是1,1+3=4
……
于是就这么以8为间隔，一批一批递增上去，就是ans

手撕代码，虽然不好想，但是如果能观察也就还可以，慢慢熟悉打表的技巧吧！
实在观察不出来，直接就暴力解算了。

    //打表，推数学公式，挺狗的，但是就可以这么做public static int fightTableLeastBags(int n){if (n < 0) return -1;if (n == 0) return 0;//n取6和8，ans=1//n取12,14和16，ans=2//其余全部ans=-1if (n <= 17) return n == 6 || n == 8 ? 1 :n == 12 || n == 14 || n == 16 ? 2 : -1;//n取18开始**逢奇数n全-1**if (n % 2 != 0) return -1;//逢偶数n，ans会分组以4个相同的数字递增出现//类似这样：3 3 3 3//4 4 4 4//5 5 5 5//每一次ans是多少呢？(n-18) / 8  + 3//8个数一批，从0 1 2 3叠加到3上，就是数字递增的规律return (n - 18) / 8 + 3;}public static void test2(){for (int i = 1; i <=50 ; i++) {System.out.print(i +":"+ minBagWithoutRules(i));System.out.println();//打印出前100看看System.out.print(i +":"+ fightTableLeastBags(i));System.out.println();//打印出前100看看}}public static void main(String[] args) {
//        test();test2();}

1:-1
1:-1
2:-1
2:-1
3:-1
3:-1
4:-1
4:-1
5:-1
5:-1
6:1
6:1
7:-1
7:-1
8:1
8:1
9:-1
9:-1
10:-1
10:-1
11:-1
11:-1
12:2
12:2
13:-1
13:-1
14:2
14:2
15:-1
15:-1
16:2
16:2
17:-1
17:-1
18:3
18:3
19:-1
19:-1
20:3
20:3
21:-1
21:-1
22:3
22:3
23:-1
23:-1
24:3
24:3
25:-1
25:-1
26:4
26:4
27:-1
27:-1
28:4
28:4
29:-1
29:-1
30:4
30:4
31:-1
31:-1
32:4
32:4
33:-1
33:-1
34:5
34:5
35:-1
35:-1
36:5
36:5
37:-1
37:-1
38:5
38:5
39:-1
39:-1
40:5
40:5
41:-1
41:-1
42:6
42:6
43:-1
43:-1
44:6
44:6
45:-1
45:-1
46:6
46:6
47:-1
47:-1
48:6
48:6
49:-1
49:-1
50:7
50:7

如果n非常大时，暴力找贼慢的，你自己整代码试试就知道
当使用打表技巧时，这个速度就是o(1)的查找速度，仅此而已，非常非常快！

总结

提示：重要经验：

1）打表技巧比较有趣，遇到题目，先暴力贪心解题，根据解题的代码，打印一批结果，观察看看结果有没有规律，有规律就可以打表了。
2）打表的公式可能不太好推导，但是咋说呢，尽量观察推公式吧，打表的速度可是o(1),飞快的。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。