ARM中多寄存内存访问概念和栈的种类和应用

本文主要是介绍ARM中多寄存内存访问概念和栈的种类和应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

多寄存器内存访问指令

• @ 多寄存器内存访问指令
  @ MOV R1,#1
  @ MOV R2,#2
  @ MOV R3,#3
  @ MOV R4,#4
  @ MOV R11,#0x40000020
  @ STM R11,{R1-R4}
  @ 将R1-R4寄存器中的数据存储到内存以R11为起始地址的内存中
  @ LDM R11,{R6-R9}
  @ 将内存中以R11为起始地址的数据读取到R6-R9寄存器中
  @ 当寄存器不连续是使用逗号分隔
  @ STM R11,{R1,R2,R4}
  @ 不管花括号里的顺序如何，存储时永远是低地址存储小编号的寄存器
  @ STM R11,{R3,R1,R4,R2}
  @ 自动索引照样适用多寄存器内存访问指令
  STM R11!,{R1-R4}

多寄存器内存访问指令的寻址方式

• @ 多寄存器内存访问指令的寻址方式
  @ MOV R1,#1
  @ MOV R2,#2
  @ MOV R3,#3
  @ MOV R4,#4
  @ MOV R11,#0x40000020
  @ 存储完数据在增长地址
  @ STMIA R11!,{R1-R4}
  @ 先增长地址在存储数据
  @ STMIB R11!,{R1-R4}
  @ 先存储玩数据在减少地址
  @ STMDA R11!,{R1-R4}
  @ 先减少地址在存储数据
  @ STMDB R11!,{R1-R4}

栈的种类和应用

• 栈的概念
  栈的本质就是一段内存，程序运行时用于保存一些临时数据
  如局部变量、函数的参数、返回值、以及程序跳转时需要保护的寄存器
• 栈的分类
  
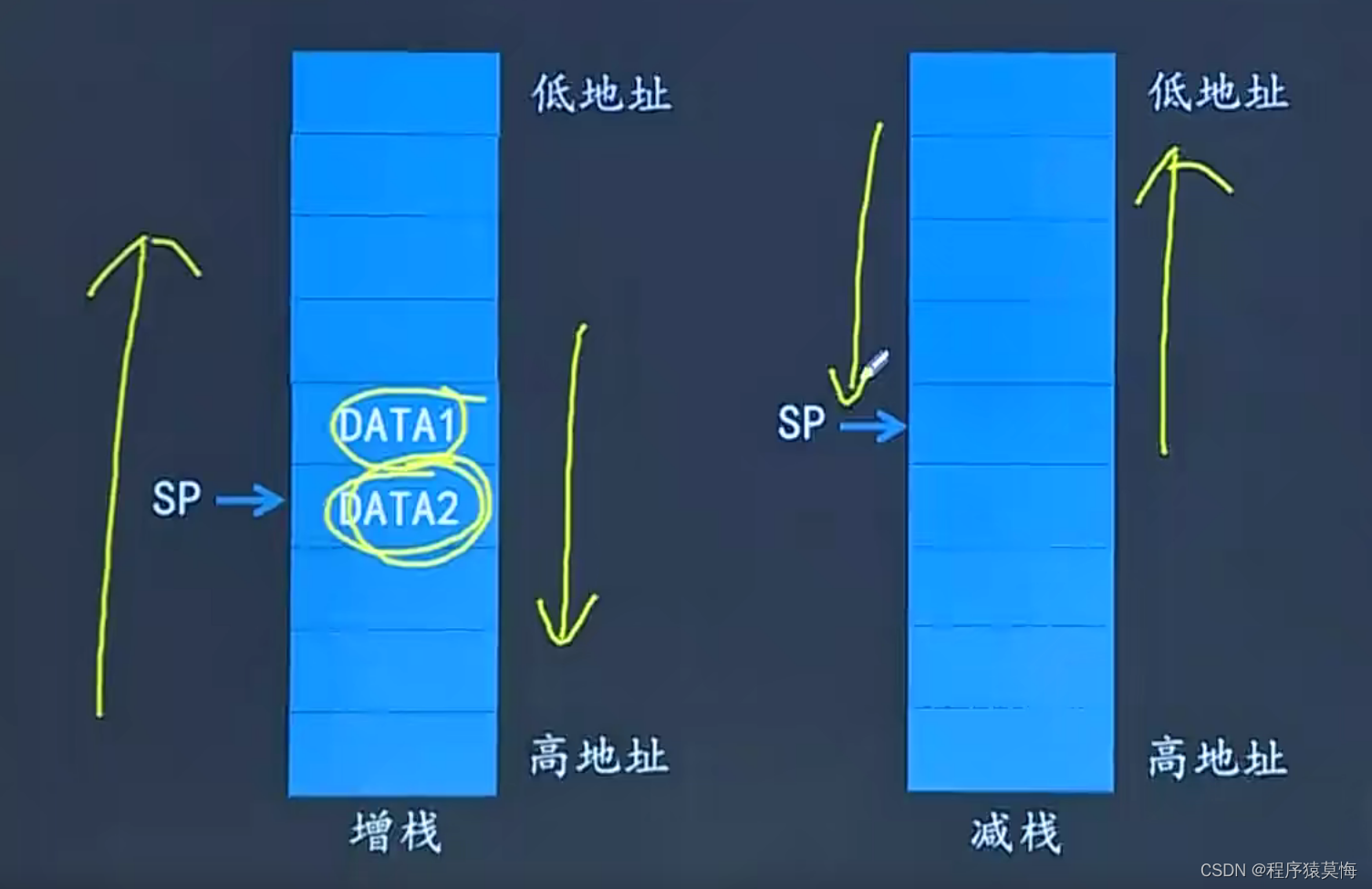
• 空栈和满栈
  根据SP位置来区分，如果空栈的话，先压栈在移动指针，反之如果满栈的话，先移动指针，在压栈
• 栈的分类
  栈分为空增、空减、满增、满减四种，ARM处理器一般使用满减栈(和之前的STMDB类似，减是往地址小的方向压栈)
• 代码指令如下：
  @ 栈的种类与使用
  MOV R1,#1
  MOV R2,#2
  MOV R3,#3
  MOV R4,#4
  MOV R11,#0x40000020
  STMDB R11!,{R1-R4}
  LDMIA R11!,{R6-R9}
• ARM内部一般用字母来表示满增、满减等等
  空增(EA)、空减(ED)、满增(FA)、满减(FD)
• 汇编代码如下：
  MOV R1,#1
  MOV R2,#2
  MOV R3,#3
  MOV R4,#4
  MOV R11,#0x40000020
  STMFD R11!,{R1-R4}
  LDMFD R11!,{R6-R9}
• 叶子函数的调用过程举例
  @ 初始化栈指针
  @ MOV SP,#0x40000020
  @MAIN:
  @ MOV R1,#10
  @ MOV R2,#5
  @ BL FUNC
  @ LDMFD SP!,{R1,R2}
  @ ADD R3,R1,R2
  @ B STOP
  @FUNC:
  @压栈保护现场
  @ STMFD SP!,{R1,R2}
  @ MOV R1,#10
  @ MOV R2,#20
  @ SUB R1,R2,R1
  @ MOV PC,LR
• 非叶子函数的调用过程举例
  @ 初始化栈指针
  MOV SP,#0x40000020
  MAIN:
  MOV R1,#3
  MOV R2,#5
  BL FUNC1
  ADD R3,R1,R2
  B STOP
  FUNC1:
  STMFD SP!,{R1,R2,LR}
  MOV R1,#10
  MOV R2,#20
  BL FUNC2
  SUB R1,R2,R1
  LDMFD SP!,{R1,R2,LR}
  MOV PC,LR
  FUNC2:
  STMFD SP!,{R1,R2}
  MOV R1,#7
  MOV R2,#8
  MUL R3,R1,R2
  LDMFD SP!,{R1,R2}
  MOV PC,LR

这篇关于ARM中多寄存内存访问概念和栈的种类和应用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---