万丈高树平地起：通过中序与后序遍历数组构建二叉树

本文主要是介绍万丈高树平地起：通过中序与后序遍历数组构建二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

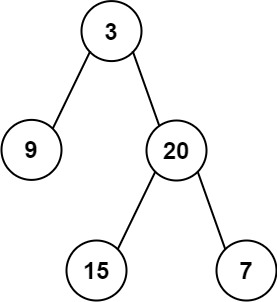
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

思路

前、中、后序三种遍历方式是二叉树经典的三种遍历方式，一般通过给定的二叉树来写出遍历后的结果，同样反过来给定后序和中序，也可以反推出二叉树的完整结构。

构建二叉树的第一步就是找到此二叉树的根节点，而直接看中序遍历无法找出根节点的所在位置，而按后序遍历的顺序来看，根节点就是位于最后一个位置的值，而紧跟着往前一个，肯定就是根节点right所指向的节点，再往前就是根所指right的left的值，依次类推就可以一个个找出按后序遍历依次进入数组的节点的值，但依然无法准确的知道其具体位置，此时结合中序遍历，先找到根节点，左边的就是根的左子树，右就是根的右子树。依次往下就可以构建出树。

代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int &previ,int begin,int end){if(begin>end) return nullptr;int cur=begin;TreeNode* root=new TreeNode(postorder[previ--]);while(inorder[cur]!=root->val)//找到根在中序中的位置{++cur;}root->right=_buildTree(inorder,postorder,previ,cur+1,end);//建立左树root->left=_buildTree(inorder,postorder,previ,begin,cur-1);//建立右树return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int begin=0,end=inorder.size()-1;int previ=end;//从后进行往前遍历TreeNode* root=_buildTree(inorder,postorder,previ,begin,end);return root;}
};

这篇关于万丈高树平地起：通过中序与后序遍历数组构建二叉树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---