本文主要是介绍蓝桥杯备赛 day2 | 4. 付账问题 5. 数字三角形,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
付账问题,关键是要了解整型的范围,确定获取输入数据的变量类型

 需要注意的是int的十进制范围
需要注意的是int的十进制范围-32768 ~ 32767,那么我们可以知道,人数n是可以用int来装的,需付款数S应该是long long,获取的每个人初始钱数也应该是long long
同时,由于最终结果才要求用小数,在中间计算里尽量不要出现除法(如果可以的话),避免除法丢失精度
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
static bool comp(const long long & a,const long long & b){return a < b;
}
int main(){long long n;long long s;cin>>n>>s;vector<long long> money;for(auto i = 0;i< n;i++){long long a;cin>>a;money.push_back(a);}sort(money.begin(),money.end(),comp);double avg = 1.0 * s / n ;double sum = 0.0;for(auto i = 0;i< n;i++){if(money[i] * (n-i) < s){sum+= (money[i] - avg) * (money[i] - avg); s -= money[i];}else{double finalAvg = 1.0 * s / (n-i) ;sum += (finalAvg -avg)*(finalAvg -avg)* (n-i);break;}}printf("%.4lf",sqrt(sum / n));return 0;
}
不过这道题很奇怪,判题系统在我使用变量S的时候判错,把变量S改为小写的s就正确了;double avg = 1.0 * s / n ;这种语句,1.0在后面乘也是错的,改个顺序又没事了,没搞懂。。。


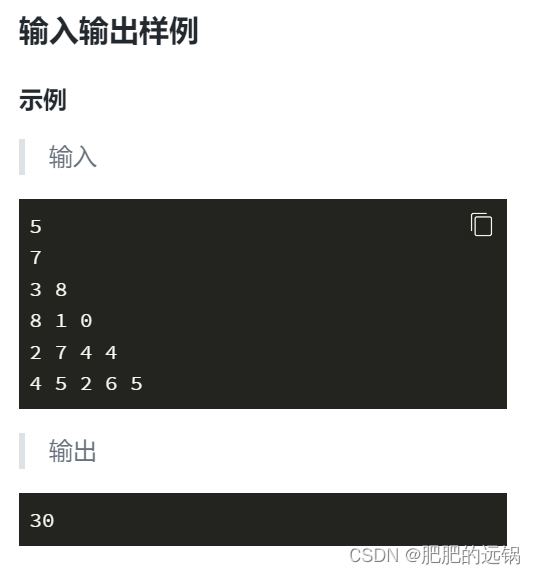
这道题一开始想着数据量小,直接回溯法,没想到这都能超时,只能从回溯递归的暴力解改回动态规划了(不过我这个不是很熟,可以大概讲讲暴力->dp的修改思路)
首先,暴力回溯是有可能不断走前几轮已经走过的路径的,如果强行算下去实际的时间复杂度O(n!)很大,无法接受。这个时候使用dp,其实就是把已经经历过的状态都记录下来,当再次经历这个状态时,就从dp的状态表里获取已有的数据,这样相当于把计算量大大削减,时间复杂度甚至可以到O(n)
想要把算法实现从暴力回溯改到dp,实际上就是从自顶向下的递归改到自底向上的递推,或是从自底向上的递归改到自顶向下的递推。我们首先要找出递归算法中原问题和子问题的自变量是啥,也就是状态,比如dfs里面的自变量就是横纵坐标i和j,然后实际的结果是啥(这个一般就是题目要你求的解,也是你递归函数最后在返回时要得到的东西),那么dp状态表我们就可以知道了,有一个状态,dp状态表就是一维的,两个就是二维,dp[i][j]表示i和j状态变化可以得到的某某结果
然后在dp状态表里填入base case,这就是看是从自顶向下的递归改到自底向上的递推,或是从自底向上的递归改到自顶向下的递推,前者的base case就在后面(因为要改成自底向上的递推),后者就是在前面因为要改成自顶向下的递推)
状态转移方程就看你的递归函数的实现,其实就是递归的逆过程,递归的各个状态咋倒回来
可以看看我这道题的解法,一开始是用的dfs递归,后续写了一个逆过程递推函数traceback,体会一下
#include<bits/stdc++.h>
#include<iostream>
using namespace std;vector<vector<int>> matrix;
vector<vector<int>> dp;
vector<int> nextVec;
int res = INT_MIN;
void resInit(int n){for(int i = 0;i< n;i++){vector<int> vec(n,0);matrix.push_back(vec);dp.push_back(vec);}for(int i = 1;i<= n;i++){for(int j = 0;j< i;j++){cin>>matrix[i-1][j];if(i == n){dp[i-1][j] = matrix[i-1][j]; }}}for(int i = 0;i< 2;i++){nextVec.push_back(i);}}
void traceback(int & n){//base case 在dp初始化时已经做好 -> 第n-1行for(int i = n-2;i>= 0;i--){for(int j = 0;j< n;j++){if(i+1 < n && j+1 < n){dp[i][j] = max(dp[i+1][j] + matrix[i][j],dp[i+1][j+1] + matrix[i][j]);}else if(i+1 < n && j+1 >= n){dp[i][j] = dp[i+1][j] + matrix[i][j];} }}}/*void dfs(vector<int> & chooseList,int sum,int i,int j,int & n){if(i < 0 || i> n-1 ){res = (res < sum) ? sum : res;return; }for(int c : chooseList){dfs(chooseList,sum+matrix[i][j],i+1,j+c,n);}return;
}*/int main(){int n;cin>>n;resInit(n);//dfs(nextVec,0,0,0,n);// printf("%d",res);traceback(n);printf("%d",dp[0][0]);return 0;
}
这篇关于蓝桥杯备赛 day2 | 4. 付账问题 5. 数字三角形的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









