模具设计----哈夫模(Open die)设计要点浅谈

模具设计----哈夫模(Open die)设计要点浅谈

前言：

当遇到图1中的零件的时候，往往会采用一种特殊的模具结构，如图2，可以叫做分片模或者哈夫模。在设计工艺时，类似于图1中的零件，由于杆中间处的法兰大于杆的直径， 不仅要考虑成形得到所需的零件形状，更要考虑如何将零件从模具中取出。为此，工程师们便开发出这样的一种模具结构。通常这种模具结构都包含一个可以张开和闭合的分片模、一个供分片模活动的外圈、一个用于使分片模张开的销钉、一个用于将分片模顶出使其被销钉张开的顶出器、以及一个在成形过程中使闭合好的分片模轴向运动的弹性元件。其运动过程大致是：首先分片模在冲模的作用下闭合形成成形的型腔，之后冲模继续下行，弹性元件收缩，工件开始成形，冲模回程时，在顶出器的作用下，分片模逐渐被打开，最后零件被顶杆顶出，其运动过程可以从图3中得到大致了解。

图1 零件示意图

图2 分片模示意图

图3 分片模运动示意图

正文

从图3中，可以看到要使分片模能够正确的运动，要有正确的设计参数。从图中可以看到分片模有一个锥度θ，这个锥角就是一个设计参数；相邻的分片模之间有一个斜槽，而这个斜槽的角度δ也是一个设计参数；分片模从张开到闭合的轴向移动距离∆h也是一个设计参数，它决定了能否将工件取出，与之对应的还有一个径向移动距离∆r，这是在垂直于轴线的横截面上从闭合到张开的过程中的分片模的径向移动距离，∆h与∆r有一定的函数关系，即知道其中任意一个值就可求出另一个值。同时销钉的直径d，销钉的长度l，也是设计参数，不同于前几个设计参数，这两个设计参数更多的是取决于分片模的实际结构，之后将会有一个例子进一步解释。

分片模的设计参数包括：

1. 锥角θ，通常这个角度取15°
2. 轴向移动距离∆h或径向移动距离∆r
3. 斜槽角度δ
4. 以及销钉直径d和销钉长度l（与具体结构有关）

在这里不做任何解释，直接给出分片模的运动曲线：分片模从闭合到张开过程中，任意对应位置的连线均为一个与主轴共平面且夹角为θ的空间直线，且分片模的每一片的对称面处的外壁均始终贴合外圈的内壁。

如图4可知，

∆r = ∆h∙tanθ

以四片模为例，图5是垂直轴线某个横截面处四片模闭合和张开状态图，图中的D是一个关键的数据，它是张开状态时形成的内接圆，只有当D大于要取处工件部分的最大外径才能将工件取出，也就是D最小值就是取处工件部分的最大外接圆直径。当确定了D以后，就确定了∆r，从而就确定了∆h。设r为闭合状态下分片模的最小内径。图6是图5中E的放大图，使用这个图来分析它们之间的关系：

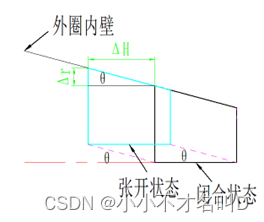
图4 分片模单个片对称面处的几何关系图

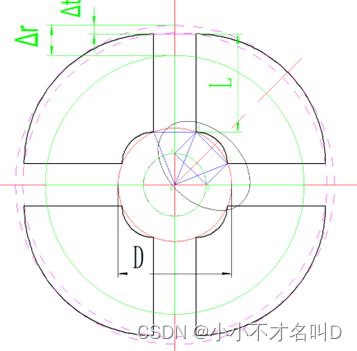
图5 垂直轴线某个横截面处四片模闭合和张开状态图，黑色张开状态，绿色闭合状态

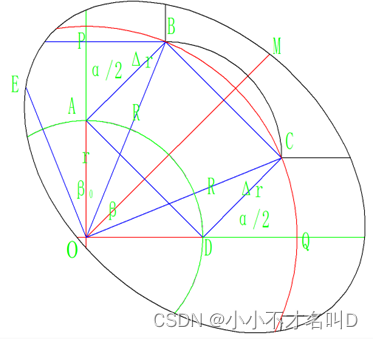
图6 图5中E的放大图

图中OB =OC = R(张开时工件取出半径R = D/2)，OA = OD = r(闭合时最小内径)，AB = DC= ∆r(径向移动距离)，∠PAB = α/2，AB // OM // DC。令∠EOB = β0，∠BOC = β，∠EOP = ∠POB = ∠COD = β0/2，∠ABO = ∠BOM = ∠MOC = β/2。以上关系均可由AP // OM // DC平行关系和对称关系证明，故不再具体证明，感兴趣读者的可自行证明。

在三角形△AOB中，由三角形余弦定理可得：

R^2 = r^2 + ∆r^2 − 2∙r∙∆r∙cos(180-α/2)

即：

R=sqrt( r^2 + ∆r^2+ 2∙r∙∆r∙cos⁡(α/2))

∆r= sqrt(R^2 + 0.5r^2(cosα-1))-rcos(α2)

sqrt()开根号的意思

在三角形△AOB中，由三角形正弦定理可得：

R/sin(180-α/2) = r/sin(β/2) = ∆r/sin(β0/2)

β = 2arsin(r*sin(α/2)/R)

β0 = α − β

△BPA为直角三角形，所以开口宽度w

w = 2∙∆r*sin(α/2)

由图7可知，轴向移动距离∆h与开口宽度w以及斜槽角度δ满足(要想产生R，必须移动特定的∆h，必须由δ角张开w宽)

tan(δ) = w/(2∙∆h) = sin(α/2)∙tan(θ)

即

δ = arctan(sin(α/2)∙tan(θ))

可知，对一个确定的分片模结构，δ是一个定值，即无论模具的具体结构尺寸如何，只要采用相同的α与θ，δ都是一样的。

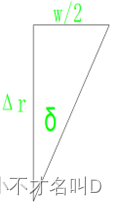
图7 ∆h与开口宽度w以及斜槽角度δ的关系

对于销钉直径d和销钉长度l这两个参数是与分片模的具体尺寸有关的。销钉的作用是使分片模张开w的宽度，因此销钉要始终在斜槽里面滑动不脱出，因此销钉有一个最小的伸出距离∆lmin，如图8，即图6中的∆t，。由图6可得

∆lmin = (r0 + ∆r) –(Rcos(β0/2) + L)

r0---该截面内闭合状态下分片模的外径，其中L = r0 – r。

∆lmin = ∆r + r –Rcos(β0/2) = ∆h∙tanθ+ r –Rcos(β0/2)

故装配好的销钉至少要伸出的∆lmin距离。

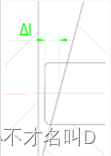
图8 销钉伸出距离

对于销钉的直径d，这个是自己设计的，大小合适即可。但销钉有一个最小的直径dmin，当设计的直径小于dmin时，当移动∆h距离时，销钉会滑出斜槽。

dmin = 2∆h∙sin(δ)

即销钉的直径要大于dmin。

现假设分片模小端面直径为D，高度为H，销钉距离分片模大端面的距离为h0，销钉滑动槽的高度为hd，宽度为Wd，如图9所示。其之间满足以下关系：

hd = h0 + d/(2sin(δ))

Wd = 2∙hd∙tan(δ)

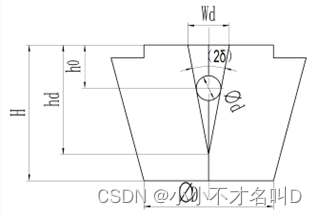
图 9分片模尺寸、销钉直径及相对位置图

分片模的参数设计总结：

（1）锥角θ，通常这个角度取15°

（2）轴向移动距离∆h，∆r

∆r= sqrt(R^2 + 0.5r^2(cosα-1))-rcos(α2)

∆r = ∆h∙tanθ

（3）斜槽角度δ

δ = arctan(sin(α/2)∙tan(θ))

（4）以及销钉直径d和销钉长度l（与具体结构有关）

∆lmin = ∆r + r –Rcos(β0/2) = ∆h∙tanθ+ r –Rcos(β0/2)

dmin = 2∆h∙sin(δ)

       如果可以的话实际伸出量可取3∆lmin，销钉总长取整。

       若符合图9中结构，可计算出hd，Wd

hd = h0 + d/(2sin(δ))

Wd = 2∙hd∙tan(δ)

（5）一些中间参数

R=sqrt( r^2 + ∆r^2+ 2∙r∙∆r∙cos⁡(α/2))

β = 2arsin(r*sin(α/2)/R)

β0 = α − β

w = 2∙∆r*sin(α/2)

以上的分析虽然使用四片模为例，但上述公式适用于任何片数的分片模。读着可自行证明。

从上面可以看到，当确定了θ，α时，δ是一个定值。表1给出来了θ = 15°时，δ与α的关系。

表1 θ = 15°时，δ与α的关系

α	δ
120°	13.0643°
90°	10.7286°
72°	8.9504°
60°	7.6307°
45°	5.8546°

设计流程

如图10，

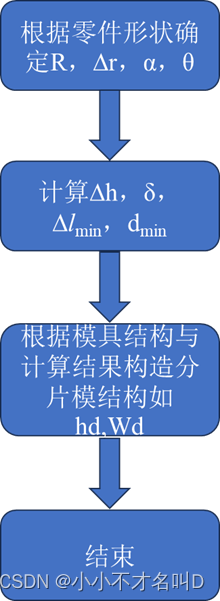
图10 分片模设计流程

计算案例

假设有一个零件如图11，从图中可以看到，这个零件需要使用分片模结构才能够成形。现假设直径为11的球需要使用分片模结构成形。

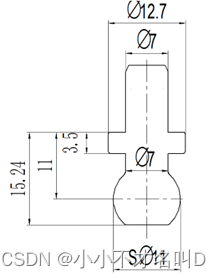
图11 设计案例

计算步骤：（长度单位均为mm，角度单位均为度，除不尽的均保留4位小数）

1. 根据图10中的流程图，需要首先确认R，α，θ，∆r。

（a）决定采用四片模的结构，即α = 90；

（b）按照通常的习惯去θ = 15；

（c）由图10可知，要想将零件取出，四片模张开时的内接圆直径至少是11，

     一般设计值要比最小值大一点，这里取R = 5.6。

（d）再由图11可知，四片模闭合时的最小直径为7，即r = 3.5,由此可计算得到   
∆r= sqrt(5.6^2 + 0.5*3.5^2(cos90-1))-3.5*cos45=2.5486

1. 根据图10中的流程图，之后计算∆h，δ，dmin，∆lmin。

∆h = 2.5486/ tan(15) = 9.5115

δ = 10.7286

                     计算中间参数

β = 2*arsin(3.5*sin(45)/5.6) = 52.4557

β0 = 90 – 52.4557 = 37.5443

w = 2*2.5486*sin(45) = 3.6042

                 计算dmin，∆lmin

dmin = 2*9.5115*sin(10.7286) = 3.5413

∆lmin = 9.5115*tan15+ 3.5 –5.6*cos(37.5443/2) = 0.7465

1. 如图12，假设四片模的小端直径为21，高度为22，销钉直径为4，距离大端面的距离为7。则：

hd = 7 + 2/sin(10.7286) = 17.7436

Wd = 2*17.7436*tan(10.7286) = 6.7237

图13给出了一个销钉直径为8的计算结果

hd = 7 + 4/sin(10.7286) = 28.4872

Wd = 2*28.4872*tan(10.7286) = 10.7948

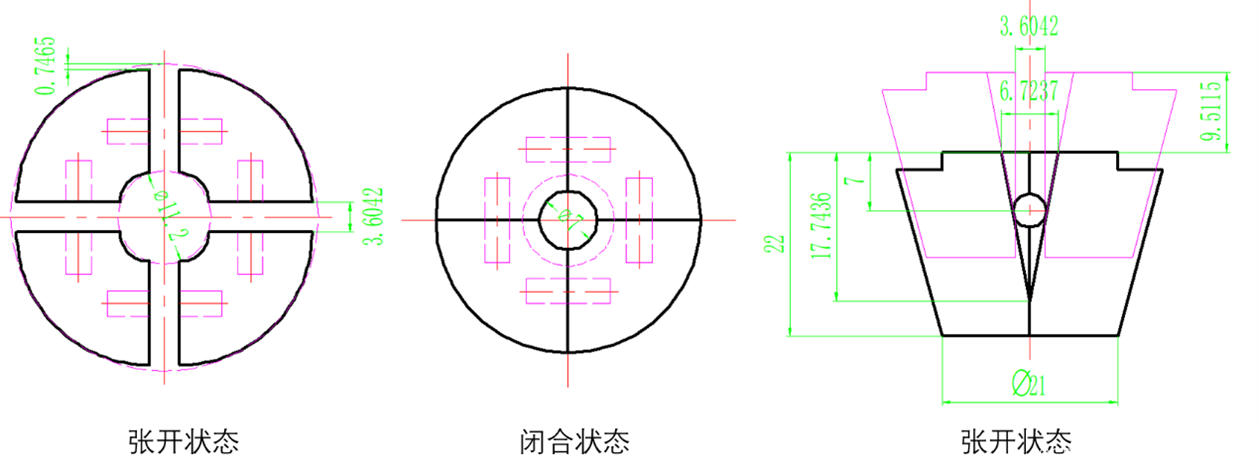
图 12 销钉直径4mm时的分片模状态图

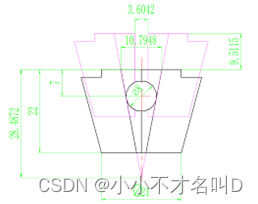
图13 销钉直径8mm时的分片模状态图

探讨

图14是图13的一种装配示意图，从图中可以看到，一共存在两种弹性元件。一个是分片模外套下的弹性元件，另一个是顶出器下的弹性元件。两个弹性元件的作用各不相同。顶出器下的弹性元件主要是使分片模张开，弹力需要克服摩擦阻力。分片模外套下的弹性元件起到两个作用：（1）提供足够的初始载荷使分片模完全闭合。（2）在完全闭合以后提供成形阶段的行程。通常希望外套在分片模未完全闭合时是不运动的，如果弹性元件的载荷不足以克服闭合时的阻力，就会使外套运动，从而在工件上沿合模线造成飞边（如果完全闭合后依然有飞边，在保证强度的前提下，减少相邻片模之间的接触面积，增大接触压强。）。理论上这个所需的初始载荷是可以计算的，但是又难以计算，即便是借助运动学仿真也是难以计算。因此在设计的时候，在允许的条件下使用能提供最大初始载荷的弹性元件。

对于模具的材料选择，并没有很好的推荐。只是说明一点，在成形时外套主要承受的是膨胀力，即具有周向拉应力，因此材料应具有较高的抗拉强度同时又具备较高的韧性。同时在制作的过程中，运动的表面应具有较高的表面状态和形状。

图14 闭合时示意图

结语

在上面对分片模的运动以及设计参数做了一系列的推导，目的是使人们能够更加直观的理解这种模具结构，不至于使刚接触的人感到茫然。虽然需要采用这种结构的场景各不相同，同时受限于条件结构的实现形式也会不同，但只要是使用这种结构，有了这些推导过程，都可以提供一个清晰的认识。但也不能直观的认为掌握了这些理论知识就能够十分的熟练的设计，这只是一个基础，还需要大量的实践才能够使自己更加的完善（比如弹性元件的选择，模具材料的选择，模具结构的实现形式等）。最后我也会不断的更新与完善，最终开发出相应的辅助设计软件，目前仅存在初版软件。

声明：

文中所使用的部分图片与视频来源于互联网上的资源，非常感谢提供这些资源的人与机构。