本文主要是介绍Codeforces Round 930 (Div. 2)题解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A. Shuffle Party(Problem - A - Codeforces)
题目大意:给定一个n长数组,并使得a[i]=i,现在定义一种操作swap(k):找出k的最大不等于自己的除数d,交换a[k]和a[d],k从1开始直到n结束,问最后结束的时候1在哪里。
思路:这题的交换看似比较混乱,但是我们如果只盯着1的位置就会发现规律。1可以换到位置2,而位置2只能换到位置4,位置4换到位置8,...,所以实际上我们只要找到n在二进制下最高位1即可。
n在1e9的范围内,我们可以从30开始循环,往低位找。(注意int的数据范围在2^31-1的范围内,所以也就是说int类型的数最多31位,如果从32开始循环就会出现错误)
有两个二进制处理:
获取n的第i位是否是1,判断n>>i&1是否为1,如果为1,就说明n的第i位为1,否则就是0.
将最高位1后面的全部换成0:n>>i<<i,假设n的最高位1在第i位。
#include<bits/stdc++.h>
using namespace std;
int main()
{int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);int flag=1;for(int i=30;i>=0;i--){if(n>>i&1) {flag=n>>i<<i;break;}}printf("%d\n",flag);}
}B. Binary Path(Problem - B - Codeforces)
题目大意:现在有一个2行m列的方格阵,每个格子中的值是0或1,我们要从(1,1)到(2,n),每次只能向右或者向下移动一格,问字典序最小的移动方案数。
思路:这题我第一反应就是数字三角形模型+背包问题统计方案数,但也正是因为这个走入了误区,因为很显然这里是每个格子是不能将其中的数视为权重的,如果将0和1视为权重,那么就会出现两种字典序不同的方案最后的花费相同,很显然不符合题意,但是由于我没有跳出第一映像重新分析,就非得找到一个合适的dp的方法,绕来绕去最后实在没辙跑去看第三题了,浪费了不少时间,最后写出来的时候没卡上点。
这题和一般的dp问题不同,因为只能向右或者向下走,所以一旦向下走了就只能向右走了,剩下的步数就只有一种选择了,所以问题的核心在于什么时候向下走。
当我们还在上面的时候,每一步实际面临两种选择,一种是向右走,一种是向下走,字典序相同的时候方案不同那么我们看一下为什么会出现这种情况:
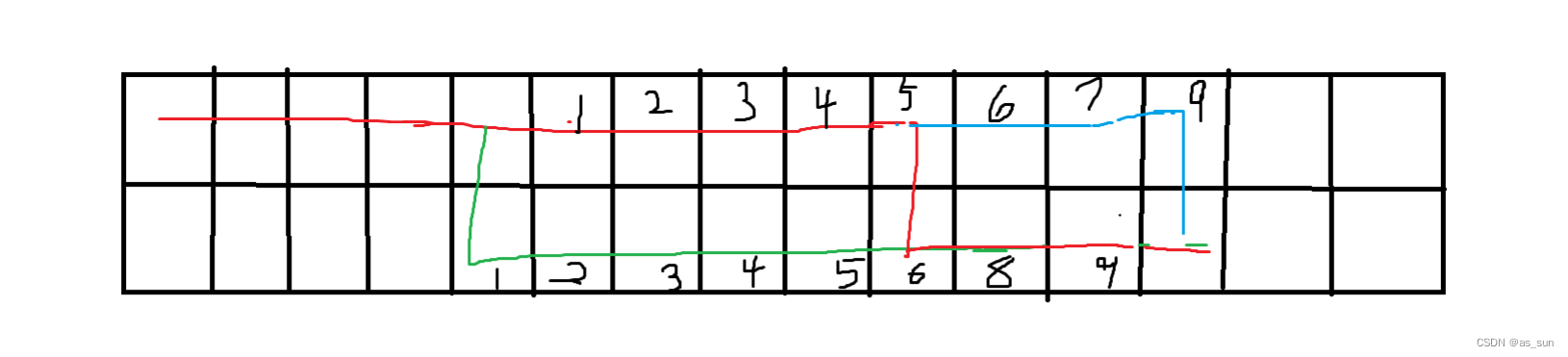
如图,如果三条路径对应的字典序相同,那么标号相同的位置的值必须相同。所以实际上我们只需要找出这样的一段区间即可。那么该怎么找呢,我们可以直接比较这样的格子,也可以比较上面一行向右和向下对应的两个格子是否相等。这里采用第二种方法,因为对输出序列友好一些,然后我们来看具体如何统计:
如果两步操作对应的格子的数是一样的,那么实际上是无所谓的,如果右边是0,下面是1,那么必须向右,前面已经统计的向右向下相等的位置的数目必须作废,如果右边是1,下面是0,那么必须向下,后面的讨论也就没有意义了。所以实际上我们只用一格一格往后找,当向右向下相同的时候计一下数,当两者不同,向右为0的时候重新计数,向下为0的时候直接退出。然后还有一点需要考虑,我们需要输出最后的序列,所以还要统计相等的那一段区间。
#include<bits/stdc++.h>
using namespace std;
char s[3][200010];
int dp[3][200010];
int n;
int main()
{int t;scanf("%d",&t);while(t--){scanf("%d",&n);for(int i=1;i<=2;i++) scanf("%s",s[i]+1);int c=0,i,l=0,r=0;for(i=1;i<n;i++){if(s[1][i+1]==s[2][i]) c++,r++;else if(s[1][i+1]>s[2][i]) break;else c=0,r=l=i+1;}if(i<=n){for(int j=1;j<=i;j++) printf("%c",s[1][j]);for(int j=i;j<=n;j++) printf("%c",s[2][j]);}else{printf("%s",s[1]+1);printf("%c",s[2][n]);}printf("\n%d\n",c+1);}
}C. Bitwise Operation Wizard(Problem - C - Codeforces)
题目大意:这题是交互题,实际上想让我们实现的是,通过询问若干次a|b与c|d的大小,进而找出异或值最大的两个数。
思路:这题也是我最开始的分析太过片面了,我只考虑了高位1,两个数的异或值大就说明两个数高位是不同的,a|b>c|d,就说明我们可以从a,b中选一个实际生效的数,从c,d中选一个没在|运算高位1中生效的数,然后就此推断出找出最大值和最小值进行异或,但是我忽略了1111111101,01,10这种情况。这种情况下显然选01不如选10。那么这道题该如何考虑呢?
我们还是想办法从这道题的特殊的地方入手,题目中给的数组是一个排列,从0到n-1的排列,那么最大的数显然是n-1,然后要找出n-1为0的哪些位置为1的数,显然两者进行|运算的值应该最大,但是如果仅仅是找或运算的话,那么n-1为1的位置,且找到的数对应位置也为1的位置的那种值如何排除呢,显然我们的目标值中1的个数最少,目标值为1的位置所有找到的值对应的位置应该也是1,但是应该比目标值大。所以就要找到所以值中最小的一个。比较两个数的大小可以通过询问a,a,b,b来得到。
#include<bits/stdc++.h>
using namespace std;
int main()
{int t;scanf("%d",&t);while(t--){int n;scanf("%d",&n);if(n==2){printf("! 0 1\n"),fflush(stdout);}else{char op[2];int mx=0,mi=0;//找最大值for(int i=1;i<n;i++){printf("? %d %d %d %d\n",mx,mx,i,i),fflush(stdout);scanf("%s",op);if(op[0]=='<') mx=i; }for(int i=1;i<n;i++){printf("? %d %d %d %d\n",mx,mi,mx,i),fflush(stdout);scanf("%s",op);if(op[0]=='<') mi=i;else if(op[0]=='=') {printf("? %d %d %d %d\n",mi,mi,i,i),fflush(stdout);scanf("%s",op);if(op[0]=='>') mi=i;} }printf("! %d %d\n",mx,mi),fflush(stdout);}}
}
D. Pinball(Problem - D - Codeforces)
题目大意:有一排格子,每个格子中只有'<'和'>'两种字符,有一个小球被放入了第i个格子,如果格子中是'<'那么小球下一秒就会往左移动一格,同时当前格子的字符变成'>',另一种字符同理,问小球放在每个格子的时候离开格子需要多少秒。(1<=n<=5e5)
思路:如果可以模拟的话显然这题不太难,但是n的数据范围太大了,而且还有多组测试样例,很显然不能通过模拟来写,那么就要找一下规律了。
我们先只来看相邻的两个格子,而且将小球放在第一个格子处,
如果是>>,直接向右两步
如果是<<,直接向左一步
如果是><,向右一步,向左两步
如果是<>,直接向左一步。
很显然对于同向的格子可以一直沿着这个方向往前,对于反向的格子>>>><,第一次走到反向位置时,会发现已经变成了<<<<<,所以又可以一直往左。
><<<>>><
>>>>>>><
<<<<<<<<
<<<>>><
抽象一下,如果走到反向位置后,相当于可以将反向位置同化,最后至少有一端是全部被同向化了。起始方向的方向需要统计反向的个数,起始反向的方向需要统计同向个数
统计位置和(下标和处理一下)与个数
两个方向都统计一下
如果是>的话,那么要么左右阻碍个数相同,从右边出,要么左边的阻碍比右边少1个,从左边出
如果是<的话,要么左右阻碍个数相同,从左边出,要么右边的阻碍比左边少1个,从右边出
多余的阻碍可以不用考虑。
>:
cntl[i]>=cntr[i]:左右各考虑最近的cntr[i]个阻碍
cntl[i]<cntr[i]:左边考虑cntl[i]个阻碍,右边考虑最近的cntl[i]+1个阻碍
<:
cntl[i]<=cntr[i]:左右各考虑最近的cntl[i]个阻碍
cntl[i]>cntr[i]:右边考虑cntr[i]个阻碍,左边考虑最近的cntr[i]+1个阻碍,
倒是可以用单调队列统计,
看上去要实现对应位置的查找很麻烦,但实际上我们可以用前缀和+二分的思想来实现。
尽管如此细节处理还是很麻烦。
#include<bits/stdc++.h>
using namespace std;
#define int long long
char s[500010];
int l[500010],r[500010];
int cntl[500010],cntr[500010];
signed main()
{int t;scanf("%lld",&t);while(t--){int n;scanf("%lld",&n);scanf("%s",s+1);for(int i=1;i<=n;i++){if(s[i]=='>'){cntl[i]=cntl[i-1],cntr[i]=cntr[i-1]+1;l[i]=l[i-1],r[i]=r[i-1]+i;}else//<{cntl[i]=cntl[i-1]+1,cntr[i]=cntr[i-1];l[i]=l[i-1]+i,r[i]=r[i-1];}}int ans;for(int i=1;i<=n;i++){if(s[i]=='>'){//右边的< 左边的> if(cntl[n]-cntl[i]<=cntr[i-1])//从右边出,那么左边的>不会用完{//找到左边第cntl[n]-cntl[i]个>int x=cntl[n]-cntl[i];int xl=1,xr=i-1,p=xl;if(x==0) p=i;//这里会出现为0的情况else{while(xl<xr){int mid=(xl+xr)/2;if(cntr[i-1]-cntr[mid-1]<x) xr=mid-1;else if(cntr[i-1]-cntr[mid-1]>x) xl=mid+1;else xl=xr=mid;}p=xl;}//[mid,i-1]这个区间中的>ans=2*(l[n]-l[i]-x*i) + 2*(x*i-(r[i-1]-r[p-1])) + (n-i+1);}else//从左边出,需要获得右边第cntr[i-1]+1个<的位置{int x=cntr[i-1]+1;int xl=i+1,xr=n,p=xl;while(xl<xr){int mid=(xl+xr)/2;if(cntl[mid]-cntl[i]<x) xl=mid+1;else if(cntl[mid]-cntl[i]>x) xr=mid-1;else p=xl=xr=mid;}p=xl;ans = 2*(i*cntr[i-1]-r[i-1])+2*(l[p]-l[i]-(cntl[p]-cntl[i])*i)+i;}}//><<else//<{//左边的> 右边的<if(cntr[i]<=cntl[n]-cntl[i])//从左边出{//获取右边第cntr[i]个<的位置int x=cntr[i];int xl=i,xr=n,p=xl;while(xl<xr){int mid=(xl+xr)/2;if(cntl[mid]-cntl[i]<x) xl=mid+1;else if(cntl[mid]-cntl[i]>x) xr=mid-1;else p=xl=xr=mid;}p=xl;ans=2*(x*i-r[i])+2*(l[p]-l[i]-x*i)+i;}else//从右边出,这里不会出现某种值为0的情况{//找左边第cntl[n]-cntl[i]个>的位置int x=cntl[n]-cntl[i]+1;int xl=1,xr=i-1,p=xl;while(xl<xr){int mid=(xl+xr)/2;if(cntr[i-1]-cntr[mid-1]<x) xr=mid-1;else if(cntr[i-1]-cntr[mid-1]>x) xl=mid+1;else p=xl=xr=mid;}p=xl;ans = 2*(x*i-(r[i-1]-r[p-1]))+2*(l[n]-l[i]-i*(x-1))+n-i+1;}}printf("%lld ",ans);}printf("\n");}
}总结:b,c两道题都给了一个启示,看到题目先从普遍的情况去思考,当卡住的时候,不要咬死不放,想办法从这道题目特殊的地方再去思考一下。d题的启示在于从某个范围中紧邻的第x个符合要求的数的时候可以考虑前缀和+二分来实现。
这篇关于Codeforces Round 930 (Div. 2)题解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






