本文主要是介绍振动解调用的包络谱计算,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1缘起
在振动分析中,对于一些高频频点的分析计算,使用包络谱技术,进而得到特化谱是最适宜的。我们看matlab信号分析中提供的一个实例:
https://www.mathworks.com/help/signal/ug/compute-envelope-spectrum.html
轴承故障有4个故障频点,示例中模拟了一个外圈故障的数据,然后对BPFO附近的谱线进行分解,最终用于分析的BPFO特化谱在这里,外圈故障是点蚀作用,非标准正弦波,所以倍频丰富。形成的最终包络谱视图可以很清晰地看到相关故障信号的基频和倍频特征。方便进行相关的故障分析的定量和定性分析。
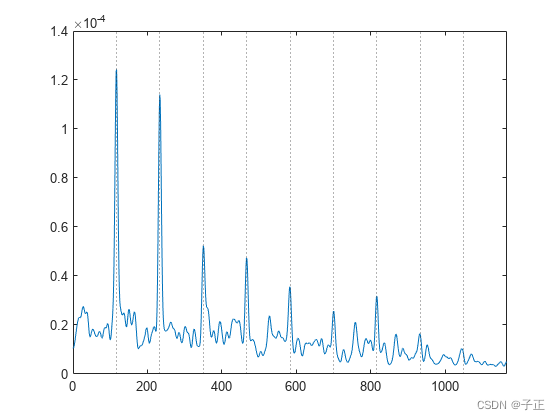
它的纵坐标有问题,最终的图理论上需要用db坐标。-40db一般认为是有效信号出现的门限。
这个问题,我看了无数的文章,看了希尔伯特变换的一篇论文,但是似乎没有人能说清楚包络变换的原理和操作步骤,很多人在进行包络计算时,只是调用了一个数学工具库中的函数。它做了什么,甚至,最终视图的坐标轴的档位都不明晰。
奇怪的是,这个重要的数学工具,在我查阅的一些标准的振动分析教材上也鲜有提及——也许它太过简单,是个常识?但关于希尔伯特变换的含义和在包络运算的使用,又确实没有几个人能说得清。感谢matlab,感谢一切在网络上积极进行理论和技术传播的从业人员和热心人士。希望和你们继续同行。
2.包络谱的计算步骤
四个步骤:
1.去零点
2.带通滤波
3.包络解调
4.去零点
然后在展示时:
5.功率谱显示
6.设置maxFreq。修饰倍频谱线位置。
3.重要步骤备注
1.为什么最终的包络谱线能达到谱线移动的效果?
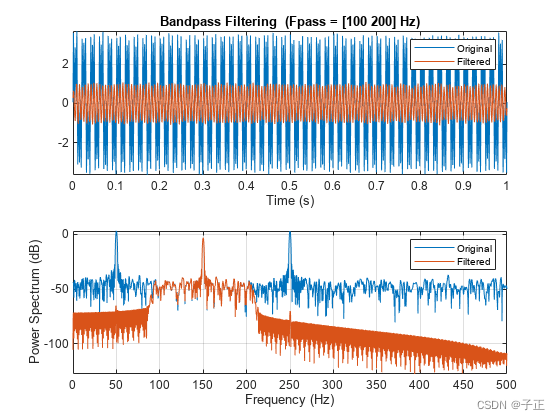
看到上面带通滤波后的红色频谱和时域图就明白了。(出处:Bandpass-filter signals - MATLAB bandpass)
经过带通之后的时域图红色的部分是个非常典型的调制波。在它的这个高频频点附近BPFO的基频和倍频以调制波上叠加低频信号呈现。因为所有关心谱线之外的频段已经都被带通滤波器抑制,所以,最终经过标准的希尔伯特envelope解调后,这段细节谱就会被移动到低频部分。
此外,注意如果使用标准的希尔伯特解调,解调前后似乎会有一个两倍幅度加乘,如果你无法使用好用的数学运算库,要注意核对最终生成的全域包络谱的幅度,要把额外的加成消掉。
附录A 各种中间波形和频谱图
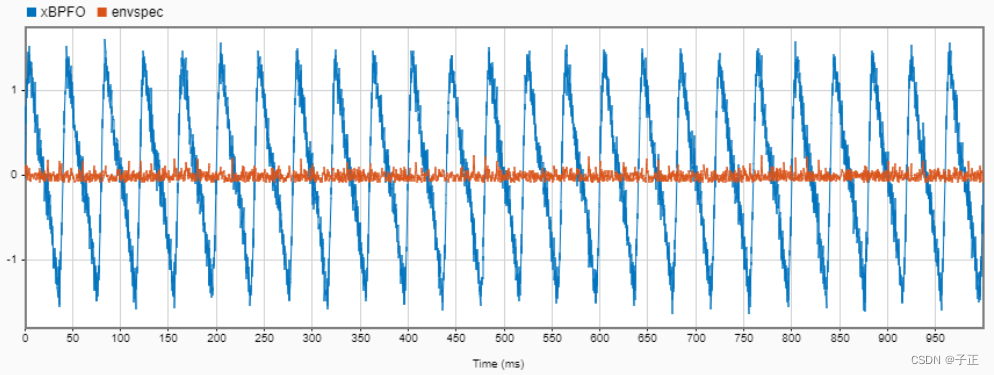
原始时域图
外圈故障是等幅的,因为只有一个BPFO在起作用,内圈故障因为滚珠和轴速接近,会呈现出幅度调制的效果。波形边缘是起伏的。
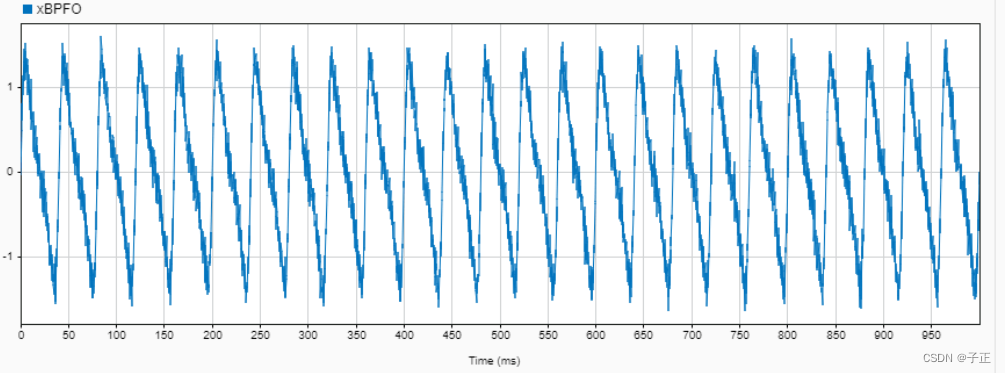
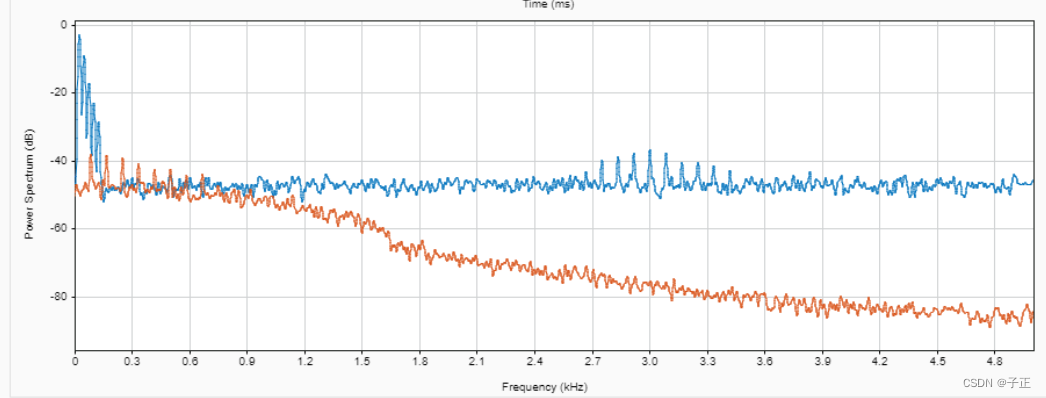
原始频域功率谱
注意3kHz的一簇梳状故障谱线,高峰已经顶过-40db。故障信号已经形成。在进行FFT变换时,特别注意变换后输出的纵坐标的单位是什么。是原始幅度值还是db这类比率坐标,它直接影响故障的初筛。
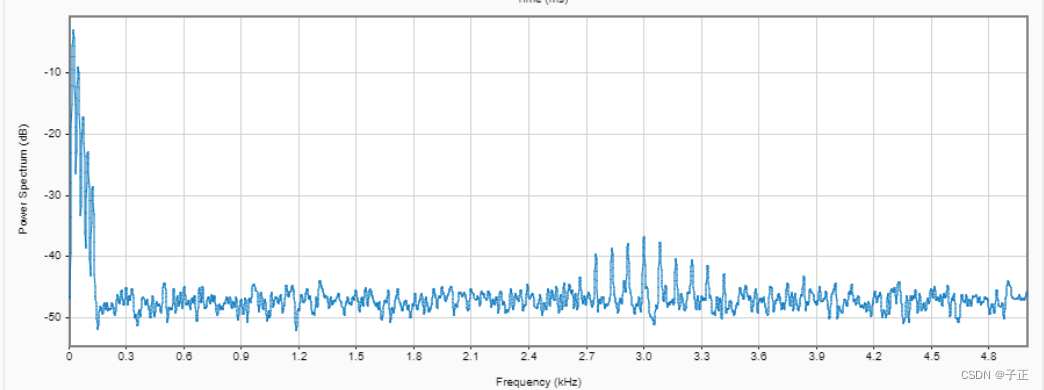
包络时域图
注意红色的故障频带幅度是很小的,样例中,这个振动信号刚刚超过-40db,是原始信号的1/100这样的量级。
包络和全频域图
这里高频的下潜部分是由带通滤波实现的,低于-40db无需分析。输出全域谱可以保留,如本文开篇那个BPFO特化谱,可以直接把低于-40db很多的无关部分消掉,不显示。
附录B 希尔伯特变换的数学和物理意义
与包络计算相关的希尔伯特变换的解析参见:
希尔伯特变换的在信号解调时的示例-CSDN博客
这篇关于振动解调用的包络谱计算的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





