本文主要是介绍Open CASCADE学习|GC_MakeArcOfCircle构造圆弧,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1、通过圆及圆的两个参数创建圆弧,参数为弧度角
2、通过圆及圆上的一点、圆的1个参数创建圆弧,参数为弧度角,Sense决定方向
3、通过圆及圆上的两个点创建圆弧,Sense决定方向
4、通过三点创建圆弧,最后一点应安排在中间,方向为P1-P3-P2
5、通过两点以及经过其中一点的切线创建圆弧
实现三维空间中圆弧的构造算法。结果是一条Geom_TrimmedCurve曲线。MakeArcOfCircle对象提供了一个框架,用于:
定义了圆弧的构造,
实现构建算法,以及
查阅结果。特别是,Value函数返回构造的圆弧。
源文件GC_MakeArcOfCircle.hxx如下:
// Created on: 1992-09-28
// Created by: Remi GILET
// Copyright (c) 1992-1999 Matra Datavision
// Copyright (c) 1999-2014 OPEN CASCADE SAS
//
// This file is part of Open CASCADE Technology software library.
//
// This library is free software; you can redistribute it and/or modify it under
// the terms of the GNU Lesser General Public License version 2.1 as published
// by the Free Software Foundation, with special exception defined in the file
// OCCT_LGPL_EXCEPTION.txt. Consult the file LICENSE_LGPL_21.txt included in OCCT
// distribution for complete text of the license and disclaimer of any warranty.
//
// Alternatively, this file may be used under the terms of Open CASCADE
// commercial license or contractual agreement.
#ifndef _GC_MakeArcOfCircle_HeaderFile
#define _GC_MakeArcOfCircle_HeaderFile
#include <Standard.hxx>
#include <Standard_DefineAlloc.hxx>
#include <Standard_Handle.hxx>
#include <GC_Root.hxx>
#include <Geom_TrimmedCurve.hxx>
class gp_Circ;
class gp_Pnt;
class gp_Vec;
//! Implements construction algorithms for an
//! arc of circle in 3D space. The result is a Geom_TrimmedCurve curve.
//! A MakeArcOfCircle object provides a framework for:
//! - defining the construction of the arc of circle,
//! - implementing the construction algorithm, and
//! - consulting the results. In particular, the
//! Value function returns the constructed arc of circle.
class GC_MakeArcOfCircle : public GC_Root
{
public:
DEFINE_STANDARD_ALLOC
//! Make an arc of circle (TrimmedCurve from Geom) from//! a circle between two angles Alpha1 and Alpha2//! given in radiians.Standard_EXPORT GC_MakeArcOfCircle(const gp_Circ& Circ, const Standard_Real Alpha1, const Standard_Real Alpha2, const Standard_Boolean Sense);//! Make an arc of circle (TrimmedCurve from Geom) from//! a circle between point <P> and the angle Alpha//! given in radians.Standard_EXPORT GC_MakeArcOfCircle(const gp_Circ& Circ, const gp_Pnt& P, const Standard_Real Alpha, const Standard_Boolean Sense);//! Make an arc of circle (TrimmedCurve from Geom) from//! a circle between two points P1 and P2.Standard_EXPORT GC_MakeArcOfCircle(const gp_Circ& Circ, const gp_Pnt& P1, const gp_Pnt& P2, const Standard_Boolean Sense);//! Make an arc of circle (TrimmedCurve from Geom) from//! three points P1,P2,P3 between two points P1 and P2.Standard_EXPORT GC_MakeArcOfCircle(const gp_Pnt& P1, const gp_Pnt& P2, const gp_Pnt& P3);//! Make an arc of circle (TrimmedCurve from Geom) from//! two points P1,P2 and the tangente to the solution at//! the point P1.//! The orientation of the arc is://! - the sense determined by the order of the points P1, P3 and P2;//! - the sense defined by the vector V; or//! - for other syntaxes://! - the sense of Circ if Sense is true, or//! - the opposite sense if Sense is false.//! Note: Alpha1, Alpha2 and Alpha are angle values, given in radians.//! Warning//! If an error occurs (that is, when IsDone returns//! false), the Status function returns://! - gce_ConfusedPoints if://! - any 2 of the 3 points P1, P2 and P3 are coincident, or//! - P1 and P2 are coincident; or//! - gce_IntersectionError if://! - P1, P2 and P3 are collinear and not coincident, or//! - the vector defined by the points P1 and//! P2 is collinear with the vector V.Standard_EXPORT GC_MakeArcOfCircle(const gp_Pnt& P1, const gp_Vec& V, const gp_Pnt& P2);//! Returns the constructed arc of circle.//! Exceptions StdFail_NotDone if no arc of circle is constructed.Standard_EXPORT const Handle(Geom_TrimmedCurve)& Value() const;
operator const Handle(Geom_TrimmedCurve)& () const { return Value(); }
private:Handle(Geom_TrimmedCurve) TheArc;
};
#endif // _GC_MakeArcOfCircle_HeaderFile
从这个文件可以看出,GC_MakeArcOfCircle提供创建圆弧的功能,构造函数可以分为两类,一类是输入圆和一些参数构造圆弧,另一类直接输入参数构造圆弧,具体如下:
1、通过圆及圆的两个参数创建圆弧,参数为弧度角
Standard_EXPORT GC_MakeArcOfCircle(const gp_Circ& Circ, const Standard_Real Alpha1, const Standard_Real Alpha2, const Standard_Boolean Sense);
2、通过圆及圆上的一点、圆的1个参数创建圆弧,参数为弧度角,Sense决定方向
Standard_EXPORT GC_MakeArcOfCircle(const gp_Circ& Circ, const gp_Pnt& P, const Standard_Real Alpha, const Standard_Boolean Sense);
3、通过圆及圆上的两个点创建圆弧,Sense决定方向
Standard_EXPORT GC_MakeArcOfCircle(const gp_Circ& Circ, const gp_Pnt& P1, const gp_Pnt& P2, const Standard_Boolean Sense);
4、通过三点创建圆弧,最后一点应安排在中间,方向为P1-P3-P2
Standard_EXPORT GC_MakeArcOfCircle(const gp_Pnt& P1, const gp_Pnt& P2, const gp_Pnt& P3);
5、通过两点以及经过其中一点的切线创建圆弧
Standard_EXPORT GC_MakeArcOfCircle(const gp_Pnt& P1, const gp_Vec& V, const gp_Pnt& P2);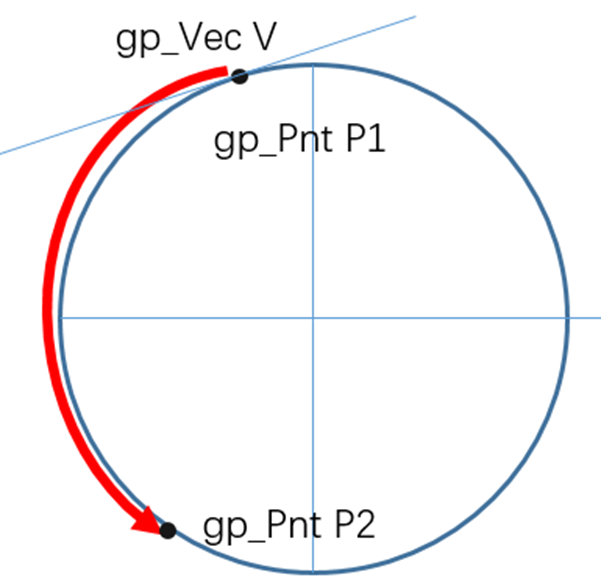
这篇关于Open CASCADE学习|GC_MakeArcOfCircle构造圆弧的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






