备考北京高考数学：历年选择题真题练一练和解析（2014-2023）

本文主要是介绍备考北京高考数学：历年选择题真题练一练和解析（2014-2023），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

还有三个多月的时间就要高考了，我们今天继续看北京市高考数学真题和解析。今天看5道选择题。独家制作的在线练习集，可以便捷地反复刷这些真题，吃透真题（背后的知识点和解题技巧），让高考数学再上一个台阶。

北京高考数学真题-选择题2022年第1题

答案选D。因为全集U={x|-3<x<3}，集合A={-2<x≤1}，所以CuA=(-3,-2]U(1,3)，故答案为D。

知识拓展：集合题目是高考的常考题目之一，通常是以选择题的出现。关于集合的常见运算知识如下：

北京高考数学真题-选择题2021年第9题

答案选C。解析如下：

北京高考数学真题-选择题2016年第6题

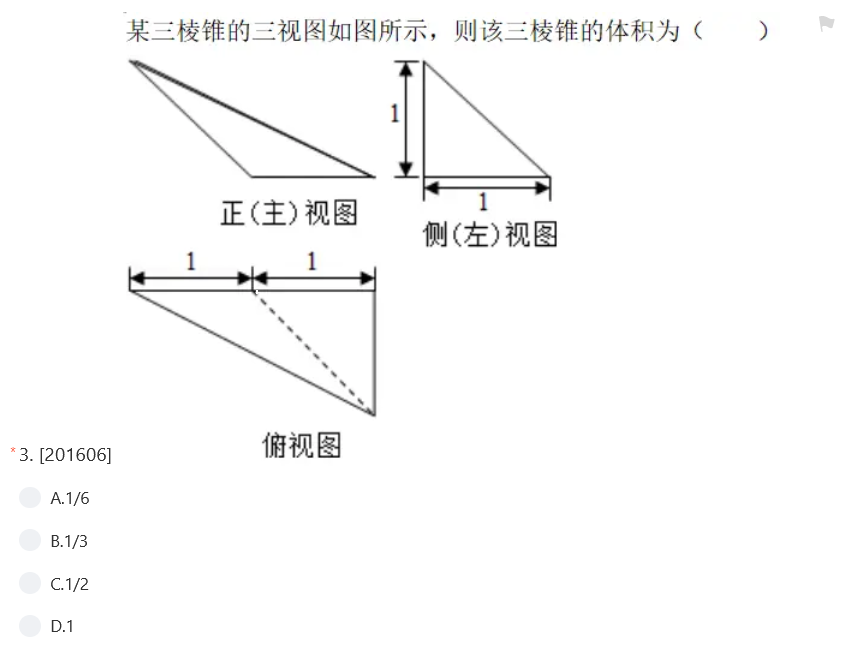
答案选A。由已题干中的三视图可得，该几何体是一个以俯视图为底面的三棱锥，棱锥的底面面积S=1/2*1*1=1/2，高为1，所以棱锥的体积V=1/3Sh=1/6。所以选A。

三视图也是高考中的立体几何常见题型，要熟练掌握。

北京高考数学真题-选择题2015年第4题

答案：B。

北京高考数学真题-选择题2014年第5题

答案：D。当q>1，数列{an}不一定是递增数列，如数列-1,-2,-4...；反之，数列{an}是递增数列，q也不一定大于1，如数列-8,-4,-2,-1...故“q>1”是“{an}为递增数列”的既不充分也不必要条件，故选D。

【知识拓展】充分必要条件也即充要条件，意思是说，如果能从命题p推出命题q，而且也能从命题q推出命题p ，则称p是q的充分必要条件，且q也是p的充分必要条件。如果有事物情况A，则必然有事物情况B；如果有事物情况B，则必然有事物情况A，那么B就是A的充分必要条件 ( 简称：充要条件 )，反之亦然。

这段时间都是用来刷题的，而根据需要老师和学霸的经验，反复刷真题是效果最好的，因为真题是最高水平的专家对照考试大纲拟定的，所以刷真题不只是追求“做过”、“知道正确答案”。而是要了解题目对应的考点（大纲知识点），以及题目涉及到的相关知识、公式、原理、解题技巧等等，并且能够触类旁通，想到类似的题目，或者题目哪里变一下，解法不一样，或者这个知识点还可以从哪些方面来考察等等。这样，就真正做到了考试题目的举一反三，也是高质量的刷真题方式。

为了帮助大家吃透这些真题，我把过去十年的真题做成了在线练习的方式，各种设备均可以流畅访问，每道题都有解析，充分用好碎片化时间、吃透真题，高考数学再上一层楼。