[Leetcode]6032. 得到要求路径的最小带权子图

【题目描述】

给你一个整数 n ，它表示一个 带权有向 图的节点数，节点编号为 0 到 n - 1 。

同时给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi, weighti] ，表示从 fromi 到 toi 有一条边权为 weighti 的 有向 边。

最后，给你三个 互不相同 的整数 src1 ，src2 和 dest ，表示图中三个不同的点。

请你从图中选出一个 边权和最小 的子图，使得从 src1 和 src2 出发，在这个子图中，都 可以 到达 dest 。如果这样的子图不存在，请返回 -1 。

子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。

示例 1：

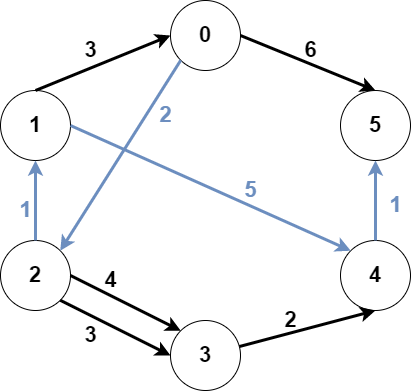
输入：n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
输出：9
解释：
上图为输入的图。
蓝色边为最优子图之一。
注意，子图 [[1,0,3],[0,5,6]] 也能得到最优解，但无法在满足所有限制的前提下，得到更优解。

示例 2：

输入：n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
输出：-1
解释：
上图为输入的图。
可以看到，不存在从节点 1 到节点 2 的路径，所以不存在任何子图满足所有限制。

提示：

• 3 <= n <= 105
• 0 <= edges.length <= 105
• edges[i].length == 3
• 0 <= fromi, toi, src1, src2, dest <= n - 1
• fromi != toi
• src1 ，src2 和 dest 两两不同。
• 1 <= weight[i] <= 105

力扣https://leetcode-cn.com/contest/weekly-contest-284/problems/minimum-weighted-subgraph-with-the-required-paths/

【思路】

        此题为有向图的最短路径问题；
        src1到dest的最短路径与src2到dest的最短路径的并集为边权和最小的子图；
        考虑到src1到dest的路径与src2到dest的路径，必然存在一个中间节点M，特殊地，M可能为src1、src2、dest其中之一；
        即src1--->M--->dest，src2--->M--->dest,src1--->M、src2--->M、M--->dest这三段路径是不重叠的；
        边权和最小的子图也即是这三段路径的之和，即dist[src1][M] + dist[src2][M] + dist[M][dest];
        那么如何找到M节点呢？
        此处可以采用遍历的方法：
        即dist[src1][M] + dist[src2][M] + dist[M][dest] = min(dist[src1][i] + dist[src2][i] + dist[i][dest]);
        
        可以采用迪杰斯特拉来求取这三段距离；
        其中i到dest的距离可以通过边方向反转，求取dest到i的苦力即可；

【代码如下】

class Solution {
public:using LL = long long;using LLV = vector<LL>;LL INF = 1e12;LLV GetDistByDijkstra(vector<vector<pair<int, int>>> adj, int src){queue<pair<int, LL>> q;LLV dist(adj.size(), INF);dist[src] = 0;q.push(make_pair(src, 0));while (!q.empty()) {auto tmp = q.front();q.pop();if (tmp.second > dist[tmp.first]) {continue;}// tmp.first称为转发节点，src到转发节点的距离为tmp.second;// 转发节点到dst的距离为adj[tmp.first]，如果经由转发节点的距离更近，那么更新src到dst的距离；for (auto& [u, d] : adj[tmp.first]) {if (d + tmp.second < dist[u]) {dist[u] = d + tmp.second;q.push(make_pair(u, dist[u]));}}}return dist;}long long minimumWeight(int n, vector<vector<int>>& edges, int src1, int src2, int dest) {LL res = INF;vector<vector<pair<int, int>>> adjEdg(n);vector<vector<pair<int, int>>> revEdg(n);for (auto& e : edges) {adjEdg[e[0]].emplace_back(e[1], e[2]);revEdg[e[1]].emplace_back(e[0], e[2]);}LLV src1Dist = GetDistByDijkstra(adjEdg, src1);LLV src2Dist = GetDistByDijkstra(adjEdg, src2);LLV dstDist = GetDistByDijkstra(revEdg, dest);for (int i = 0 ; i < n; ++i) {res = min(res, src1Dist[i] + src2Dist[i] + dstDist[i]);}return res != INF ? res : -1;}
};