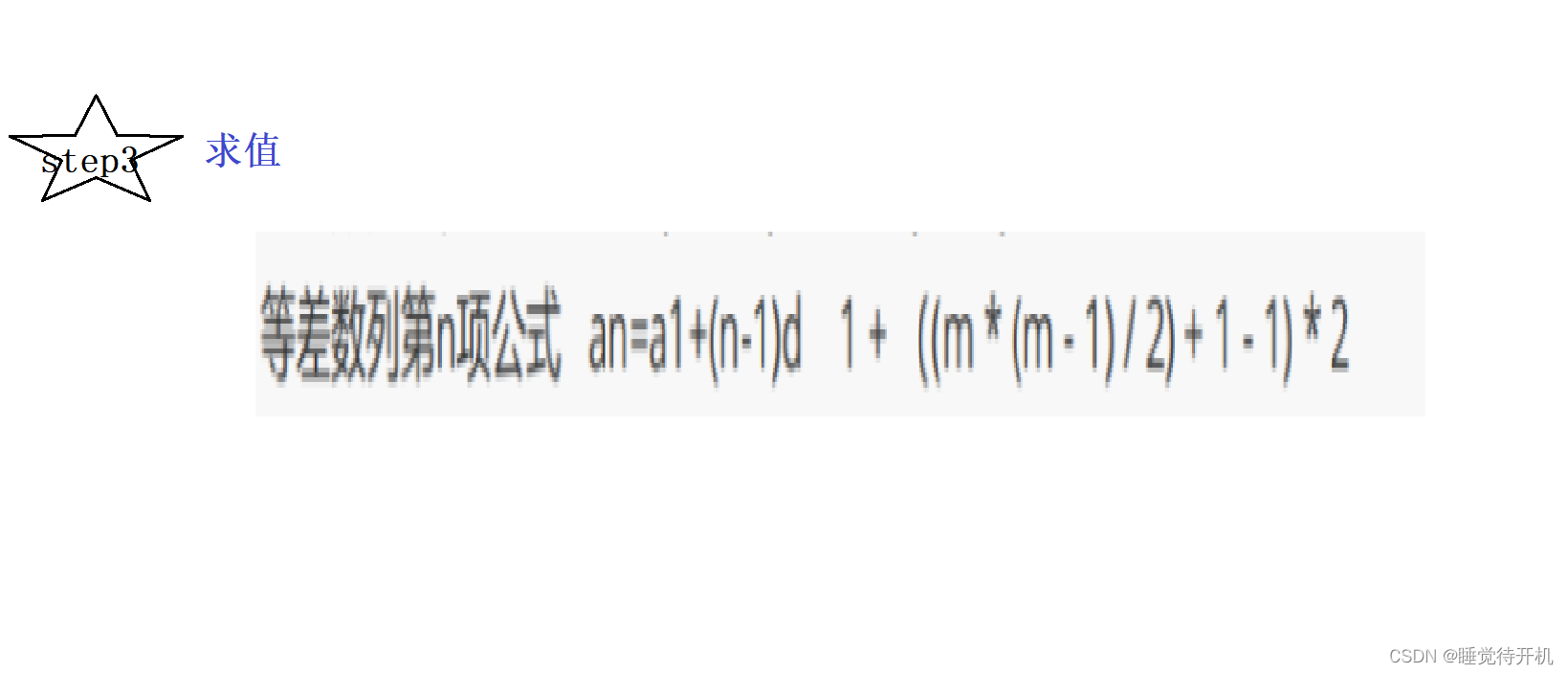【刷题记录】尼科彻斯定理、数对

本文主要是介绍【刷题记录】尼科彻斯定理、数对，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本系列博客为个人刷题思路分享，有需要借鉴即可。

今天是收集了近期遇到了两道带有鲜明的数学性质的编程题，特地整理了一下进行分享

1.题目链接：
T1:LINK
T2:LINK
2.详解思路：

T1:

思路1：
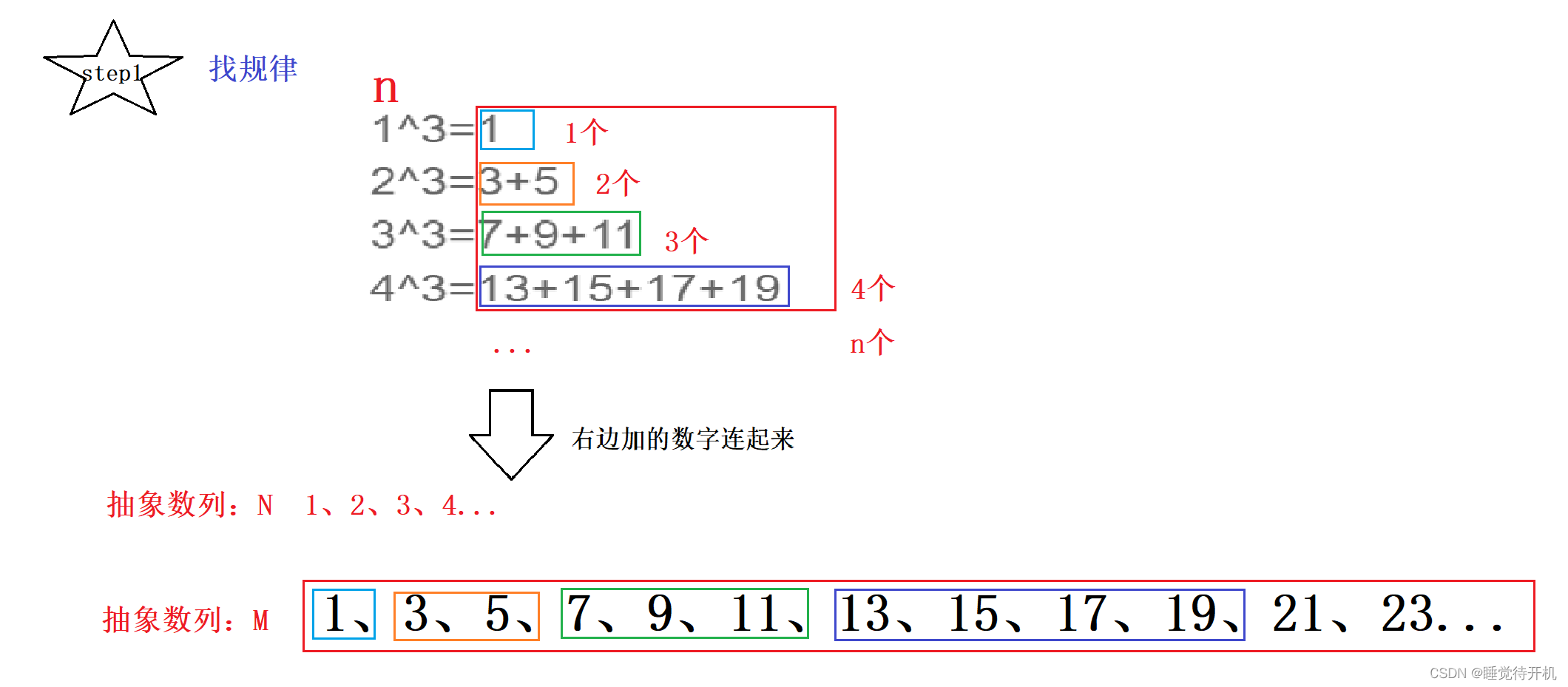
总感觉上面写的解析也能读，就是没有图不是很完善，这里就补充一下解析吧。

思路2：暴力求解，一个一个试。分析略。

下面是思路1代码示例：

#include <stdio.h>
int main()
{
int m;
while(~scanf("%d", &m)){
int start = m * (m - 1) + 1;//找到对应m^3的起始奇数
char buf[10240] = {0};
//sprintf(buf, format, ...) 与printf用法类似，格式化字符串但是不用于打印而是放到一个buf中
sprintf(buf, "%d", start);//先将起始奇数转换成为字符串存入buf中
for (int i = 1; i < m; i++) {
//然后将紧随随后的m-1个奇数数字转换为字符串，按照指定格式放入buf中
//%s+%d, 要求先有一个字符串，然后是+符号，然后是个数字的格式，对应是buf原先的数据，和奇数
sprintf(buf, "%s+%d", buf, start+=2);
}
printf("%s\n", buf);
}
return 0;
}

下面是思路2的代码示例：

#include <stdio.h>int main()
{int n;//搞个空间while (scanf("%d", &n) != EOF){int a = 0;//这是可能滴起点int sum = 0;int i = 0;int j = 0;//试一下，找到起点for (i = 73; i <= n * n * n; i += 2){sum = 0;int t = i;for (j = 0; j < n; j++){a = t;sum += t;t += 2;}if (sum == (n * n * n)){break;}}//a是最后一个值，回归最初一个值a = a - (n - 1) * 2;//输出printf("%d", a);for (i = 0; i < n - 1; i++){printf("+%d", a += 2);}}return 0;
}

T2：

这里之前看到一篇比较好的文章解析过这个题目，我这里就直接把链接放过来了。

https://blog.csdn.net/wyd_333/article/details/126640830
可以点超链接LINK

下面是代码示例：

#include <stdio.h> int main() { long n, k;     //本题中数值比较大，应用long来定义整数while(~scanf("%ld %ld", &n, &k)){ if (k == 0)     //单独判断k==0的情况{ printf("%ld\n", n * n);    //任意数对的取模结果都是大于等于0的 continue; }long count = 0; for(long y = k + 1; y <= n; y++)     //y的范围：k+1到n{ //每种情况都加起来count += ((n / y) * (y - k)) + ((n % y < k) ? 0 : (n % y - k + 1)); }printf("%ld\n", count); }return 0; 
}