Family Day/园区参观路径（C语言）

本文主要是介绍Family Day/园区参观路径（C语言），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

园区某部门举办了Family Day，邀请员工及其家属参加；
将公司园区视为一个矩形，起始园区设置在左上角，终点园区设置在右下角；
家属参观园区时，只能向右和向下园区前进，求从起始园区到终点园区会有多少条不同的参观路径。

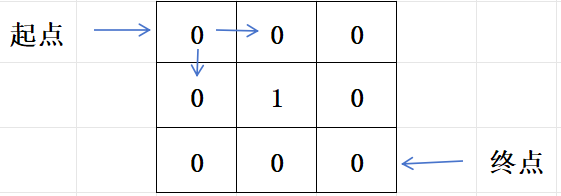
输入描述

第一行为园区的长和宽；
后面每一行表示该园区是否可以参观，0表示可以参观，1表示不能参观

输出描述

输出为不同的路径数量

用例

输入

3 3
0 0 0
0 1 0
0 0 0

输出

2

思路

动态规划（Dynamic Programming, DP）是一种在数学、管理科学、计算机科学、经济学等多领域中用于求解最优化问题的算法思想。它主要针对具有重叠子问题和最优子结构的问题，通过将复杂问题分解为相对简单的子问题，并存储并重用这些子问题的解以减少重复计算，从而得到原问题的最优解或所有可能解的数量。

在本题中，我们要求的是从园区左上角到右下角有多少种不同的参观路径。这个问题符合动态规划的应用场景：

1. 重叠子问题：在计算到达某个园区的不同路径数量时，会涉及到到达其上方和左侧园区的路径数量。例如，在计算 (i, j) 园区的路径数时，需要知道 (i-1, j) 和 (i, j-1) 的路径数，这意味着当我们计算其他位置时，可能会再次用到这些信息。

2. 最优子结构：问题的最优解可以通过组合其子问题的最优解来构造。具体来说，(i, j) 位置的路径数量等于其上方 (i-1, j) 和左侧 (i, j-1) 两个位置路径数量之和，前提是当前位置是可以参观的。

因此，我们可以采用一个二维数组 dp 来保存每个园区的路径数量，初始化时，左上角园区（起点）的路径数量为1，然后按照从上到下、从左到右的顺序遍历整个园区，根据每个园区是否可参观以及与相邻园区的关系来递推计算每个园区的路径数量。最终，右下角园区（终点）的路径数量即为所求答案。

代码

#include <stdio.h>
#include <stdlib.h>int main() {// 读取园区的行数（高）和列数（宽）int m, n;scanf("%d %d", &m, &n);// 初始化一个m×n的二维数组map，用于存储每个园区是否可以参观int map[m][n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 读取输入数据，0表示园区可参观，1表示不可参观scanf("%d", &map[i][j]);}}// 初始化一个与map同样大小的二维数组dp，用于动态规划计算不同路径数量int dp[m][n];// 动态规划遍历整个园区for (int i = 0; i < m; i++) {     // 遍历行for (int j = 0; j < n; j++) { // 遍历列// 当前园区可参观时if (map[i][j] == 0) {// 如果在起点(0, 0)，则只有一种路径（自身）if (i == 0 && j == 0) {dp[i][j] = 1;}// 如果在第一列（即只有向右的移动），则当前园区的路径数等于上一行同列园区的路径数else if (i == 0) {dp[i][j] = dp[i][j - 1];}// 如果在第一行（即只有向下的移动），则当前园区的路径数等于上一列同行园区的路径数else if (j == 0) {dp[i][j] = dp[i - 1][j];}// 对于其他园区，其路径数等于上一行同列园区路径数加上上一列同行园区路径数else {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}// 当前园区不可参观时，路径数为0else {dp[i][j] = 0;}}}// 输出从起始园区到终点园区的不同参观路径数量printf("%d\n", dp[m - 1][n - 1]); // 结束位置是(m-1, n-1)，即右下角园区return 0; // 程序执行成功返回0
}

这段代码通过动态规划的方法解决了给定问题。它首先读取矩形园区的大小以及每个园区的可访问性，然后使用二维数组dp来记录从左上角到达每个园区的不同路径数量，并根据当前位置相对于上一行或上一列园区的关系来递推计算路径数。最后输出从左上角到右下角的路径总数。

这篇关于Family Day/园区参观路径（C语言）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---