本文主要是介绍干货分享 | TSMaster 序列发送模块在汽车开发测试中的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
众所周知,序列发送模块可以不需要脚本代码实现测试中特定控制报文序列的发送,该模块多用于循环顺序控制的测试案例中。序列发送模块的常用场景,主要是针对一些新开发的产品需要通过该模块来验证产品功能等等。本文重点和大家分享一下关于TSMaster中序列发送模块的使用。
本文关键字:序列发送、无代码发送
目录
Catalog
1. 序列发送模块的使用方法
2. 序列发送模块实例
一、序列发送模块的使用方法
1、添加CAN/CANFD序列发送模块
在工具栏【测试】找到 【CAN/CANFD序列发送模块】->添加CAN/CANFD序列发送模块,如图1。

图1
2、添加新的序列发送流程
添加完成后,首先需要在序列发送窗口左侧空白处右键选择【添加新的序列发送流程】,如图2。

图2
①【切换到本序列发送流程】:存在多个序列发送流程时可以通过此选项切换流程。
②【启动序列发送流程】:启动当前选中的序列发送流程。
③【中断序列发送流程】:中断当前正在运行的序列发送流程。
④【添加新的序列流程】:创建新的序列发送流程。
⑤【编辑名称】:编辑当前选中的序列流程名称。
⑥【删除所选】:删除当前选中的序列流程。
⑦【删除所有】:删除所有序列流程。
3、添加顺序发送报文
在序列发送窗口右侧空白处右键选择添加需要序列控制的报文,可以选择新建原始报文/从数据库添加报文,如图3。
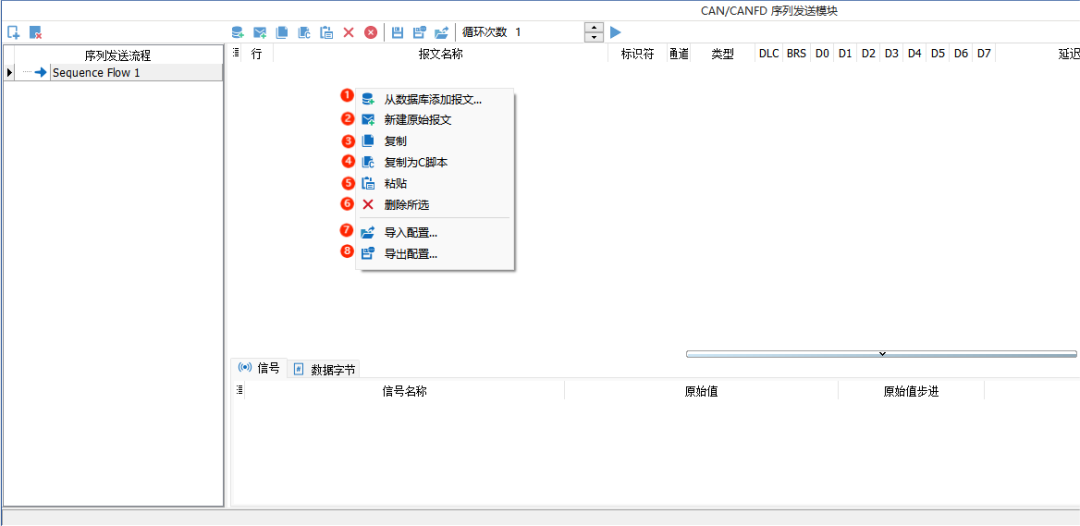
图3
①【从数据库添加报文】:加载数据库后可通过该选项添加数据库中的报文到序列发送模块中。
②【新建原始报文】:通过新建报文添加报文到序列发送模块中。
③【复制】:选择列表中的报文进行复制,再通过粘贴按钮进行粘贴。(可通过按下shift键多选报文)
④【复制为C脚本】:将当前选中的报文复制为C脚本代码。
⑤【粘贴】:粘贴已复制的报文。
⑥【删除所选】:删除选中的报文。
⑦【导出配置】:完成发送列表的配置后可以点击将该发送列表保存为.CANFDTX配置文件。
⑧【导入配置】:导入序列流程配置文件.CANFDTX
4、配置报文控制序列
按业务需求配置序列发送报文的控制数据、报文与报文间的延时时间、流程执行的循环次数,以达到我们需要的控制效果,如图4。

图4
二、序列发送实例
在汽车开发流程中,车门开闭测试是必不可少的,在这里以车门开闭控制为使用场景,讲解序列发送模块的使用。
加载数据库后通过添加数据库报文添加报文到序列发送流程中,示例中0x555报文为车门控制报文,其中包含车门控制信号定义,左前门信号:FL_Door,右前门信号:FR_Door,左后门信号:RL_Door,左后门信号:RR_Door,如图6。
> 复制多条车门控制报文,至上而下给需要控制的信号赋值。
> 对每条控制报文做相应的延时设置。
> 对已完成的序列发送流程做循环次数的配置。
> 为了方便观察控制序列发送的效果,在panal面板中添加了四个指示灯分别表示四个车门的开闭状态。
指示灯控件的属性可以非阈值模式(ThresholdMode=false,当信号值等于ValueOn所设置的值时,指示灯为点量状态,ValueOn为其他值时指示灯为熄灭状态)或选择阈值模式(阈值是指一个极限值,当某个变量达到这个值时,控件的行为会发生某种变化,将ThresholdMode的值设为True,设置阈值的高限值为1,低限值为0,当信号值等于或小于0时,指示灯为熄灭状态,当信号值等于或大于1时,指示灯为点亮状态。)如图5。

图5
完成后启动序列发送流程,指示灯代表的车门开闭状态由左前->全灭->左后->全灭->右前->全灭->右后->全灭->全亮->全灭->全亮->全灭->全亮->全灭依次循环执行100次。
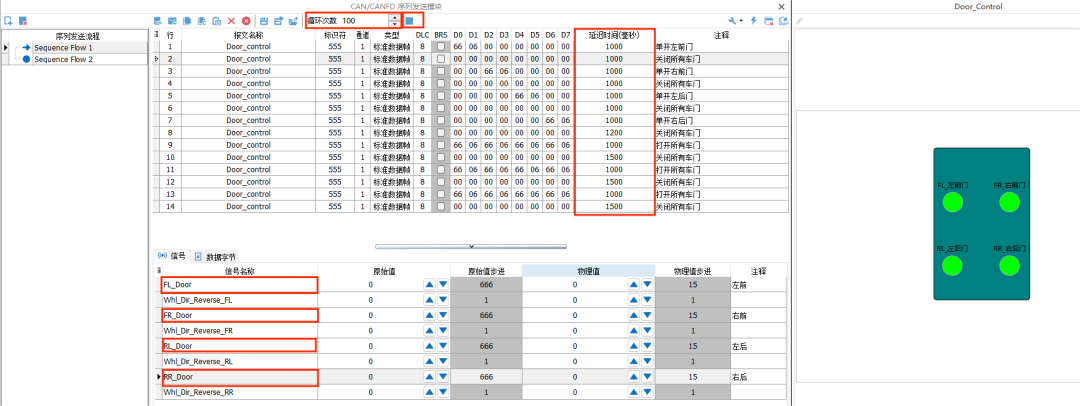
图6
以上是序列发送模块使用操作流程和示例,序列发送模块可以用于快速验证产品功能的控制效果,多个序列流程可以测试产品的多种控制状态,能熟练运用序列发送模块,将序列发送模块介入开发和测试工作中可以有效提高我们开发测试的效率。
这篇关于干货分享 | TSMaster 序列发送模块在汽车开发测试中的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




