其实这个问题已经被问烂了,但是之前没有想透,今天算是解决得差不多。
找环的入口这个问题,其实是建立在另外一个问题之上的——判断单向链表是否有环
土方法很多,但是比较好的目前就那么一个:一开始设置两个指针都指向表头,其中一个每次(一步)前进一个节点的叫p1,另外那个每次(一步)前进两个节点的叫p2 。p1和p2同时走,当其中有一个遇到null,就证明链表没有环。如何某个时刻(假设走了n步之后),p1和p2指向的地址相同,那么链表就是有环的。
接着很自然的问题就是,环的入口在哪里?
我是先看了答案,再去推导的,但是为了各位能够顺着思路,我下面就尝试用顺推的方式来展现结果,但是这样做有个不好的地方,可能有人在看完答案后会想:“我去,怎么可能想到”,这个时候由于直接看推导了,连自己推导的机会都没有,所以我建议各位先自己尝试想一下,想不出的话,你可以选择两条路:
1. 直接看答案,然后推导,答案在此【在p1和p2重合后,设置一个p3指向表头,然后p1和p3每次同时行走一步,每步前进一个节点,等到p1和p3重合时,重合的位置就是环的入口】,反选就可以看到;
2. 看顺推的过程,不知道答案,但是自己看了后也没有办法从答案推导了,因为我已经告诉你推导方法了……要走这条路的请往下拉吧……
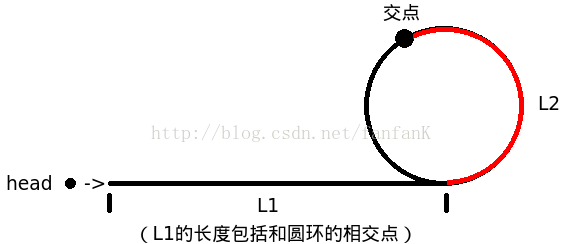
先看下面这张图:
我们设链表的无环的部分长度为L1,即有L1个节点,注意,这个L1是包括环的入口节点的。然后让环的长度是L2,这个L2也是包括环的入口节点。这个时候,p1和p2的交点如图所示,交点距离环的入口节点为a(从入口节点沿着行走方向走到交点),即在环的入口节点后面的第a个节点,就是交点,我用红色标记出a。
然后我们来考察一下L1,L2,a,以及n(n是走过的步数,不是走过的节点数,p1一步一个节点,p2一步两个节点)的关系。
忘记说一点了,我们可以明确的是,p1在进入环后,走了不到一圈就在交点处和p2重合,為什麼肯定没有走完一圈?因为p1在进入环的时候,p2和p1之间的距离(沿着行走方向)至多为 L2-1,不可能超过L2-1,因为环的大小也才只有L2 。p2追赶p1,最多只需要走L2-1步,因为每走一步,p1和p2的相对距离减小1,那么p1最多只走了L2-1步,就是最多只经过了L2-1个节点,不可能走完一圈。
现在可以列公式了:
L1+a=n #1 //n是p1走过的节点数
L1+k*L2+a=2*n #2 //2*n这个是p2走过的节点数,其中的k表示p2可能在环里面走了k圈,k>=1
由#2式减去#1式,有:
k*L2 = n #3
同时由#1和#3得到:
L1+a = k*L2 #4
接着由#4就得到了如下式:
L1 = k*L2 - a = (k-1)*L2 + (L-a)
得到这条式子就拨得云开见月明啊有木有,因为(L-a)表示的是交点与环入口的距离(从交点沿着行走方向到环入口),然后(k-1)是>=0的,因为p2在环中至少绕了一圈,这样我们就发现:L1的长度 = 环长度的整数倍 + 交点与环入口的距离
也就是说,p1再走L1步就可以达到环的入口。问题是L1不是已知的,没关系,在表头设置一个p3指针,p3每步前进一个节点。让p1和p3同时走,每次走1步,等p3和p1重合了,就是到了环口的位置了。Problem solved~