本文主要是介绍circuitJS的使用收获,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
发现一个电路设计过程中对典型电路不同R,L,C的值所带来的波形效果的仿真网站:电子森林在线工具circuitJS,下面分享一下我的使用体验和收获:
电子森林网站链接:eetree.cn/circuitjs/circuitjs.html?lang=zh
无源 RC 高通滤波器教程 - 知乎 (zhihu.com)
高低通滤波器的截止频率的计算:
高通滤波器是一种电子滤波器,它允许高于某一截止频率的信号通过,而低于该截止频率的信号则被阻止或衰减。在您提到的情况下,截止频率为30 kHz,这意味着该滤波器将允许所有频率高于30 kHz的信号通过,而阻止或衰减低于30 kHz的信号。

通过观察输入输出波形可知:RC滤波器可以滤除部分噪声,但也会给削弱输出信号幅度。
带通滤波器:输出波形呈现周期性变化,对应带通允许一定频率范围的波形通过。带通滤波器可以作为收音机等噪音的滤除硬件手段。
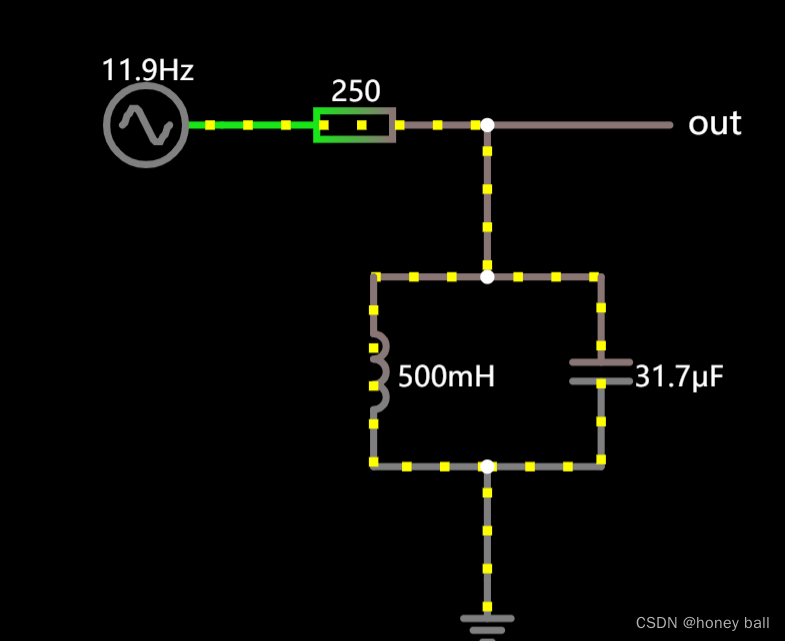
陷波滤波器(Notch Filter)是一种特殊的滤波器,它的主要作用是在一个特定的频率范围内衰减输入信号,以减少或消除该频率范围内的噪声或干扰。(示波器波形成周期性变化,衰减部分的波是其陷波的部分)陷波滤波器通常用于消除特定频率的谐波,从而只允许基波通过,方便后续的处理。这种滤波器在通信、音频处理、雷达跟踪等领域中有广泛的应用,可以有效地消除噪声、干扰信号以及时延等问题,提高信号处理的精度和可靠性。
陷波滤波器的工作原理基于共振现象。当输入信号的频率与滤波器的共振频率相匹配时,会形成谐振回路,导致滤波器损失增加并降低输出信号的幅度。因此,通过调整滤波器的共振频率,可以实现对特定频率信号的抑制。
陷波滤波器属于带阻滤波器的一种,但其阻带非常狭窄,起阶数必须是二阶(含二阶)以上。当带阻滤波器的阻带很窄时,就被称为陷波滤波器或点阻滤波器。一个理想的陷波滤波器在消除的信号频率点上的频率响应值应等于零,而在其他频率处的值应为1。
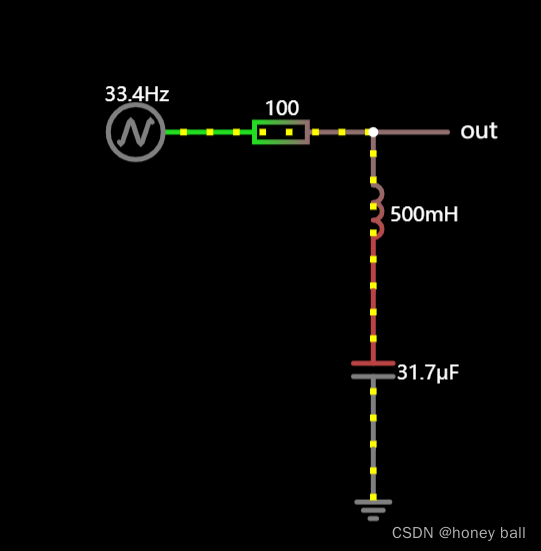
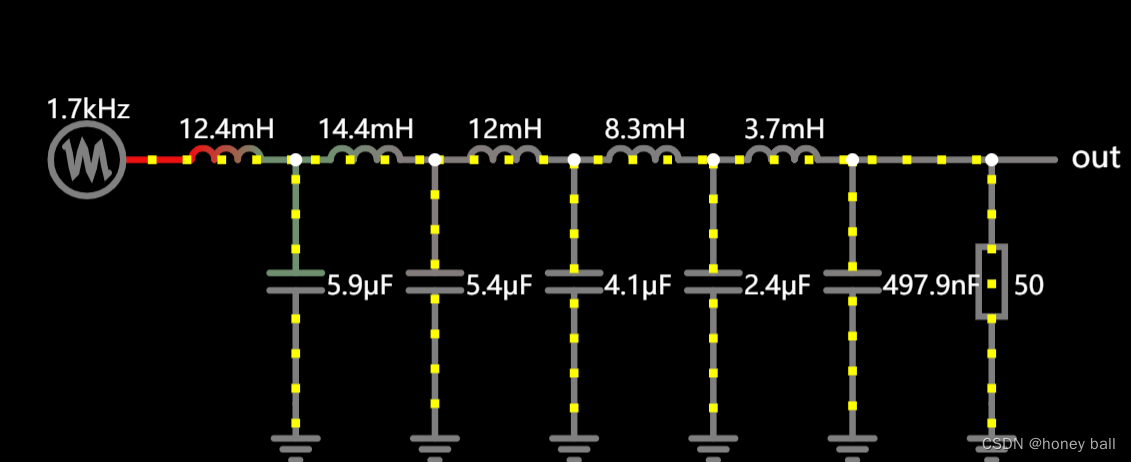
巴特沃斯低通滤波器,是一种电子滤波器,其特点是在通频带内具有平坦的幅度响应,而在截止频率以上则逐渐衰减。巴特沃斯滤波器的名称来源于其设计者在电子工程领域的贡献,它属于IIR(无限冲激响应)滤波器的一种。
巴特沃斯低通滤波器的特点是,在通带内,其频率响应曲线非常平坦,这意味着在通带内,信号的增益是恒定的,没有起伏。而在截止频率以上,滤波器的频率响应则逐渐下降,呈现单调递减的特性。这种平滑的过渡特性使得巴特沃斯滤波器在信号处理中具有广泛的应用。
巴特沃斯低通滤波器的设计涉及到滤波器的阶数、截止频率、通带增益和阻带衰减等参数。滤波器的阶数决定了滤波器的陡峭程度,即截止频率附近频率响应曲线的下降速度。阶数越高,滤波器的性能越好,但实现起来也越复杂。截止频率则是滤波器开始衰减的频率点,需要根据实际应用需求来确定。通带增益和阻带衰减则分别描述了滤波器在通带和阻带内的信号增益和衰减程度,也是滤波器设计的重要参数。
在实际应用中,巴特沃斯低通滤波器常用于平滑信号、消除噪声、提取有用信号等场景。例如,在音频处理中,可以使用巴特沃斯低通滤波器来消除高频噪声或降低音频信号的采样率;在通信系统中,可以使用巴特沃斯低通滤波器来提取基带信号或抑制带外干扰等。
全波整流:就是将幅度为负的波形部分翻上去不滤除,变为都是整的。

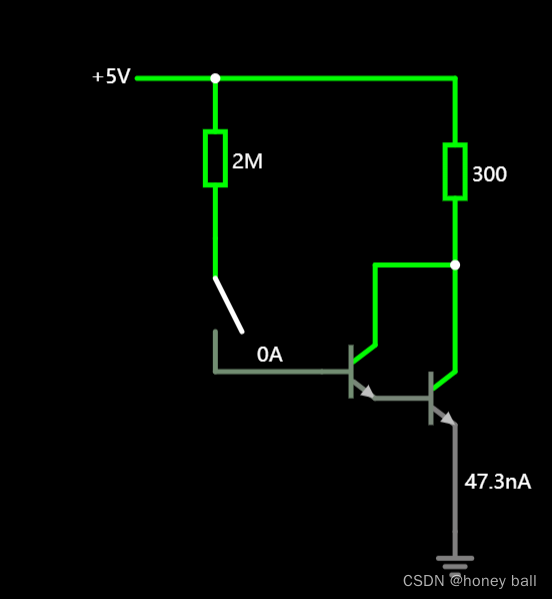
达林顿管也称为复合管,由两个三极管接在一起组成,能够放大较小的输入电流。它的放大倍数是两个三极管放大倍数的乘积,具有高放大倍数的特征,基极是电流输入端,集电极是电流输出端。见其应用于小型步进电机驱动芯片内部。
达林顿管主要用于放大电流,而不是放大电压。在需要高灵敏度放大电路的应用中,如大功率开关电路、功率放大器和稳压电源等,达林顿管常被广泛使用。同时,由于达林顿管具有高放大倍数和较高的输入阻抗等特点,它也可以用于操作继电器、直流电动机、螺线管和灯等设备。
在电子学电路设计中,达林顿接法常用于功率放大器和稳压电源中。达林顿管中的第一个晶体管在发射极跟随器模式下工作,以放大输入电流并增加输入阻抗,这允许达林顿管由普通的TTL和CMOS门电路驱动。为了使达林顿管饱和,输入电压须高于Vbe的两倍。此外,当达林顿饱和时,其C和E之间的电压需要维持第一级三极管的工作电压,该电压也比普通三极管的饱和电压(约0.2V)高得多,通常要高于0.65V。在大电流下,该电压会更高,这会大大增加达林顿管在开-关状态下的功耗。
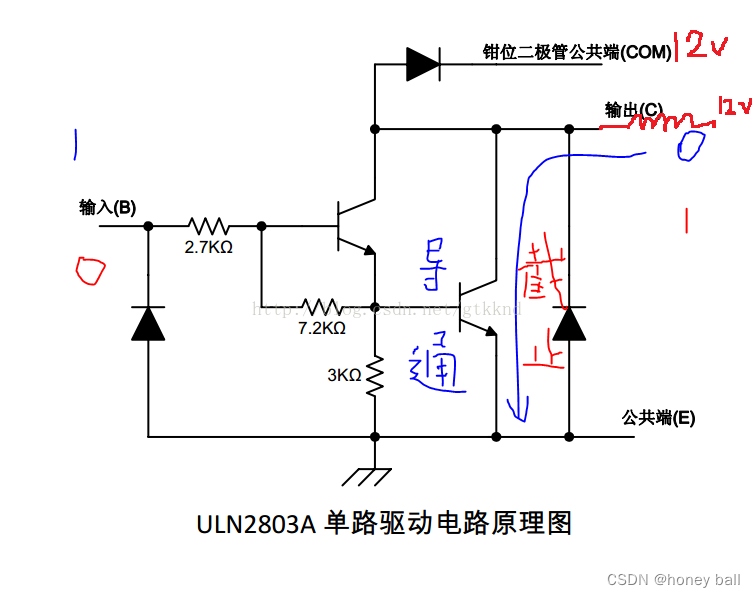
BOOST升压电路:

在开始的时候升压有一段上升期,之后保持平整。

NE555组成的施密特触发器(反相):
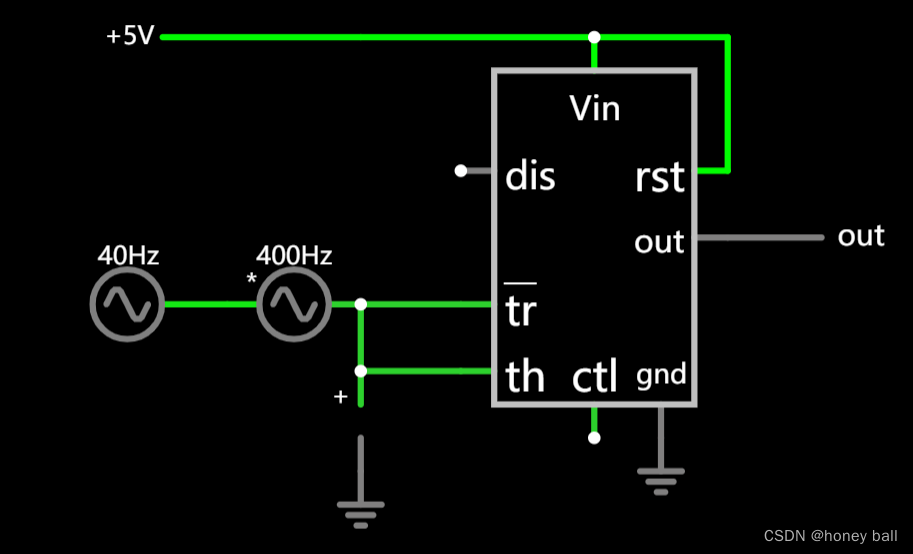
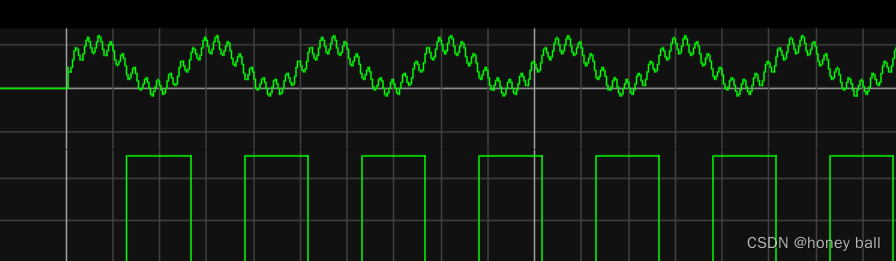
最简单的半波整流:


最简单的全波整流:

这篇关于circuitJS的使用收获的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




