Codeforces Round #688 (Div. 2) 12/4

本文主要是介绍Codeforces Round #688 (Div. 2) 12/4，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

比赛链接

T1

给出两个有序的数组，判断里面有几个相同的数，可用 $O (n + m)$ 解决。

#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define all(__vv__) (__vv__).begin(), (__vv__).end()
#define endl "\n"
#define pai pair<int, int>
#define ms(__x__,__val__) memset(__x__, __val__, sizeof(__x__))
#define rep(i, sta, en) for(int i=sta; i<=en; ++i)
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll read() { ll s = 0, w = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') w = -1; for (; isdigit(ch); ch = getchar())	s = (s << 1) + (s << 3) + (ch ^ 48); return s * w; }
inline void print(ll x, int op = 10) { if (!x) { putchar('0'); if (op)	putchar(op); return; }	char F[40]; ll tmp = x > 0 ? x : -x;	if (x < 0)putchar('-');	int cnt = 0;	while (tmp > 0) { F[cnt++] = tmp % 10 + '0';		tmp /= 10; }	while (cnt > 0)putchar(F[--cnt]);	if (op)	putchar(op); }
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1;	while (b) { if (b & 1)	ans *= a;		b >>= 1;		a *= a; }	return ans; }	ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
const int dir[][2] = { {0,1},{1,0},{0,-1},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1} };
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 100 + 7;int a[N], b[N];
int n, m;
void solve() {n = read(), m = read();rep(i, 1, n)	a[i] = read();rep(i, 1, m)	b[i] = read();int ans = 0;for (int i = 1, j = 1; i <= n and j <= m;) {if (a[i] == b[j]) ++ans, ++i, ++j;else if (a[i] > b[j])	++j;else ++i;}print(ans);
}int main() {int T = read();	while (T--)solve();return 0;
}

T2

给你起始的数组，你可以选择任意一段 $[i,n],i\in(1,n)$ ，操作一次就可以把你选择的后缀段全部元素加一或者减一。你的目标是把全部的数变成相同的，现在你有一次更改数字的机会，你可以选择一个元素 $a_i$ ，把它改成任意的值也可以保持不变，问你修改之后我们需要进行的最少操作次数是几次。
$n\leq2*10^5,|a_i|\leq5*10^8$

如果没有修改操作，我们进行修改，只需要一个倒序的循环就可以求得次数。我们就先把这个次数求到手，紧接着我们看看如果我们修改了一个数他会对答案造成什么影响。
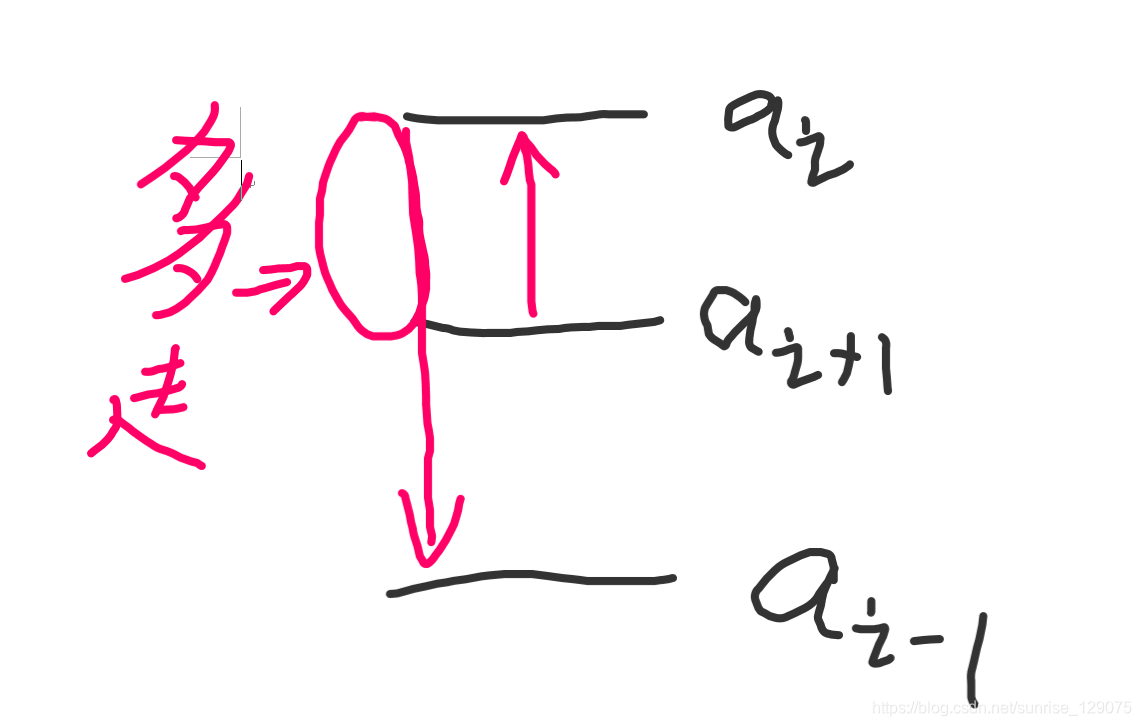
如果有一段数是1，2，3。我们去尝试修改2的话可能减少循环次数吗，显然是不行的。想象我们有3根水位线，我们要从最后一根一直收集到第一根，这样同序的排列，修改中间值不存在影响，因为你的总位移并没有变化，都是顺路捡的。但是修改 $a_1$ 和 $a_n$ 却一定可以很明显的减少循环次数，接下来的就是要修改中间部分，我们要把那种绕远路的部分去掉，那么我们画个图就可以很好看了。算到绕的最远的部分，减掉即可。
在这里插入图片描述

const int N = 2e5 + 7;int a[N];
void solve() {ll ans = 0;int n = read();rep(i, 1, n)	a[i] = read();rep(i, 2, n)	ans += abs(a[i] - a[i - 1]);int maxi = max(abs(a[2] - a[1]), abs(a[n] - a[n - 1]));for (int i = 2; i < n; ++i) {maxi = max(maxi, abs(a[i] - a[i - 1]) + abs(a[i + 1] - a[i]) - abs(a[i + 1] - a[i - 1]));}print(ans - maxi);
}

T3

给出一个n*n的0-9的数字矩阵，你可以从中间选择3个点权值相同的点，让它形成一个三角形。现在对这个三角形的要求就是有一条边平行矩阵的最左边或者最低边。现在你有一个能力，把一个地点的权值改成任何一想要的权值，当然一就要满足题目要求的矩阵，问你权值0-9构成的最大三角形面积乘以二的值是多少，依次输出。
$n\leq2000,a_{i,j}\in[0,9]$

如果我们不考虑修改操作，显然我们遍历全部相同权值的点，如果固定了一个点任何找到面积最大，显然就是同一行找最远的，构成最长的一条底边，再去它上方和下方挑更大的一边形成高。那么同一列找最远形成底边也是同理。

现在我们考虑修改操作，我们敲定一个点并且让他成为底边的一个点，我们做修改的话，一定可以选定把修改点放在底边的另一边，使得底边最大。接下来去找这个底边对应的最长的高就可以构造出最大的三角形了。因为我们会遍历到全部的点，所以每一个点都会有机会成为底边，我们并没有枚举漏掉情况。

int n, m;
int mp[2007][2007], cnt[15];
int maxx[15], maxy[15], minx[15], miny[15];void solve() {ms(maxx, -0x3f);ms(maxy, -0x3f);ms(minx, 0x3f);ms(miny, 0x3f);n = read();vector<pai> p[15];rep(i, 1, n)rep(j, 1, n) {int x;scanf("%1d", &x);mp[i][j] = x;maxx[x] = max(maxx[x], j);maxy[x] = max(maxy[x], i);minx[x] = min(minx[x], j);miny[x] = min(miny[x], i);p[x].push_back({ j,i });}rep(i, 0, 9) {if (p[i].size() <= 1) {print(0, 32);continue;}int ans = -INF;for (auto& it : p[i]) {int lenx = max(it.first - 1, n - it.first);int leny = max(it.second - 1, n - it.second);ans = max(ans, leny * max(abs(it.first - maxx[i]), abs(it.first - minx[i])));ans = max(ans, lenx * max(abs(it.second - maxy[i]), abs(it.second - miny[i])));}print(ans, 32);}puts("");
}

T4

给出闯关模型，每一道关卡你将花费1回合进行挑战，有 $\frac{1}{2}$ 的概率通过，也有 $\frac{1}{2}$ 的概率失败，如果通过你将进入下一关，如果失败，你将回到小于等于你当前关卡的出生点。现在给出你要通过的期望回合，要你给出你设计的关卡出生点位置。使得挑战者在当前概率中，通过挑战的次数期望是k，并且你给出的关卡长度小于等于2000。
$1\leq k\leq10^{18}$

下标为1的地方一定要有一个出生点，那么对于我要求的模型来说，显然是由100010100这样的由1分隔的小段组成。那么我们再看题目意思，说明只要我们到达一个新的出生点，那么之前的步骤将被固定次数，不需要考虑了。

我们从第一个出发点思考，如何计算期望，我们使用 $f_i$ 代表通过长度为 $i$ 的10串，如果 $i = 1$ 也就是1,如果 $i = 2$ ,也就是10，如果 $i = 3$ 也就是100，我们可以依次求到概率。
$f_i=f_{i-1}+1+\frac{1}{2}*f_i$
这个式子怎么理解，就是如果我通过了长度为 $i - 1$ 的10000…，如果我要继续在末尾添加一个0，那么来到第 $i$ 次挑战，我可以使用1次直接通过，如果我使用的这一次挑战机会没有成功的话失败的概率有 $\frac{1}{2}$ ，那么这 $\frac{1}{2}$ 我们就要重新回到起点，走 $f_i$ 的期望步数。约分化简之后，就会拿到。
$f_i=2*f_{i-1}+2\\f_i=2^{i+1}-2$
所以我们可以找到我们无法构造奇数的期望次数，如果是偶数的期望次数的话，因为这是一个指数函数，我们的自变量x也就是出生点数要尽可能小，所以我们要先尽可能多的用掉大的100串，这样构造就可以找到答案了。

#include <bits/stdc++.h>
using namespace std;
#define js ios::sync_with_stdio(false);cin.tie(0); cout.tie(0)
#define all(__vv__) (__vv__).begin(), (__vv__).end()
#define endl "\n"
#define pai pair<int, int>
#define ms(__x__,__val__) memset(__x__, __val__, sizeof(__x__))
#define rep(i, sta, en) for(int i=sta; i<=en; ++i)
#define repp(i, sta, en) for(int i=sta; i>=en; --i)
typedef long long ll; typedef unsigned long long ull; typedef long double ld;
inline ll read() { ll s = 0, w = 1; char ch = getchar(); for (; !isdigit(ch); ch = getchar()) if (ch == '-') w = -1; for (; isdigit(ch); ch = getchar())	s = (s << 1) + (s << 3) + (ch ^ 48); return s * w; }
inline void print(ll x, int op = 10) { if (!x) { putchar('0'); if (op)	putchar(op); return; }	char F[40]; ll tmp = x > 0 ? x : -x;	if (x < 0)putchar('-');	int cnt = 0;	while (tmp > 0) { F[cnt++] = tmp % 10 + '0';		tmp /= 10; }	while (cnt > 0)putchar(F[--cnt]);	if (op)	putchar(op); }
inline ll gcd(ll x, ll y) { return y ? gcd(y, x % y) : x; }
ll qpow(ll a, ll b) { ll ans = 1;	while (b) { if (b & 1)	ans *= a;		b >>= 1;		a *= a; }	return ans; }	ll qpow(ll a, ll b, ll mod) { ll ans = 1; while (b) { if (b & 1)(ans *= a) %= mod; b >>= 1; (a *= a) %= mod; }return ans % mod; }
const int dir[][2] = { {0,1},{1,0},{0,-1},{-1,0},{1,1},{1,-1},{-1,1},{-1,-1} };
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 60 + 7;ll n, m;
ll f[N];
void solve() {n = read();if (n & 1) { print(-1); return; }vector<int> ans;while (n) {repp(i, 60, 1) {if (n >= f[i]) {ans.push_back(1);rep(j, 1, i - 1)	ans.push_back(0);n -= f[i];break;}}}print(ans.size());for (auto& it : ans)	print(it, 32);puts("");
}int main() {f[1] = 2;rep(i, 2, 60)f[i] = (f[i - 1] + 1) * 2;//cout << f[2] << " " << f[60] << endl;int T = read();	while (T--)solve();return 0;
}

T5

给出一棵以1为根的树，要你从根节点出发，走遍每一个点，并且每个点只能走进一次，并且最终一步回到根节点1。如果两点之间的距离是两点之间边的数量，问你最大的跨越距离最小是多少。
$n\leq2*10^5$

贪心+树形dp，我们思考我们在一个过程中一定停留下来要进行长距离跳跃的时候一个起点一定是某个子树的一个叶子节点。那么我们要让这个跳跃跨越长度最小，是不是对于普通的节点来说一定要最后停留在较浅的叶子节点处，这样才方便转移到另外一颗子树上。那么我们树形dp维护每一个节点u，它距离自己最近的叶子节点之间的距离是多少。那么我们看过程对于节点u，如果它有2个及以上子树，并且它不是u=1的根节点，那么我们的贪心策略一定第一步要走进最深处，并且一步步往浅的叶子节点所在子树跳跃。那么它给答案带来的贡献就是最深的叶子节点和自己的距离+1，因为还要转移到另外一颗子树上。如果我们回到了根节点，把根节点的子树都处理完了，我们需要特殊判断一下如果根节点的最长链和次长链长度相同说明我们更新答案的时候要把次长链长度+1，当然如果最长链和次长链长度不同，我们直接选取最长链即可。最后我们的写法都分了两个以上子树，并且还使用树形dp的思维维护了一下每一个节点的距离叶子最浅距离，所以如果某个点它只有一条链的话，如果这个点不是u=1的点，那么他的dp值就会更新并且用在它的父亲身上，当且仅当整棵树是一条链的时候，我们无法更新答案这样的话，直接把链长输出即可。

const int N = 2e5 + 7;ll n, m;
vector<int> edge[N];
int ans;int dfs(int u, int fa) {if (edge[u].size() == 1 and u != 1) // 防止单链，判断叶子节点return 1;vector<int> p;for (auto& v : edge[u]) {if (v == fa)	continue;int x = dfs(v, u);p.push_back(x);}sort(all(p));int sz = p.size();if (sz > 1) { // 存在两条链if (u != 1)ans = max(ans, p.back() + 1);else // u=1的时候要注意判断下最长链和次长链相同的情况ans = max({ ans,p.back(),p[sz - 2] + 1 });}else if (u == 1) { // 如果这棵树就是一条链ans = max(ans, p[0]);}return p[0] + 1;
}void solve() {n = read();ans = 0;rep(i, 1, n)	edge[i].clear();rep(i, 1, n - 1) {int u = read(), v = read();edge[u].push_back(v);edge[v].push_back(u);}dfs(1, -1);print(ans);
}