2.18学习总结

本文主要是介绍2.18学习总结，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

链式前向星的处理和建立

tarjan对割点和缩点的使用

拓扑排序

链式前向星：

预处理：

struct edge{int from;int to;int next;
}e[N];

int n,m,head[N],dfn[N],low[N],tot,color[N],num[N],out[N],s,instack[N],id;

处理：

void add(int u,int v){	e[++tot].from=u;e[tot].to=v;e[tot].next=head[u];head[u]=tot;
}

tarjan算法求割点，以及tarjan的缩点法

割点（割顶）https://www.luogu.com.cn/problem/P3388

题目描述

给出一个 �n 个点，�m 条边的无向图，求图的割点。

输入格式

第一行输入两个正整数 �,�n,m。

下面 �m 行每行输入两个正整数 �,�x,y 表示 �x 到 �y 有一条边。

输出格式

第一行输出割点个数。

第二行按照节点编号从小到大输出节点，用空格隔开。

输入输出样例

输入 #1复制

6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6

输出 #1复制

1
5

说明/提示

对于全部数据，1≤�≤2×1041≤n≤2×104，1≤�≤1×1051≤m≤1×105。

点的编号均大于 00 小于等于 �n。

tarjan图不一定联通。

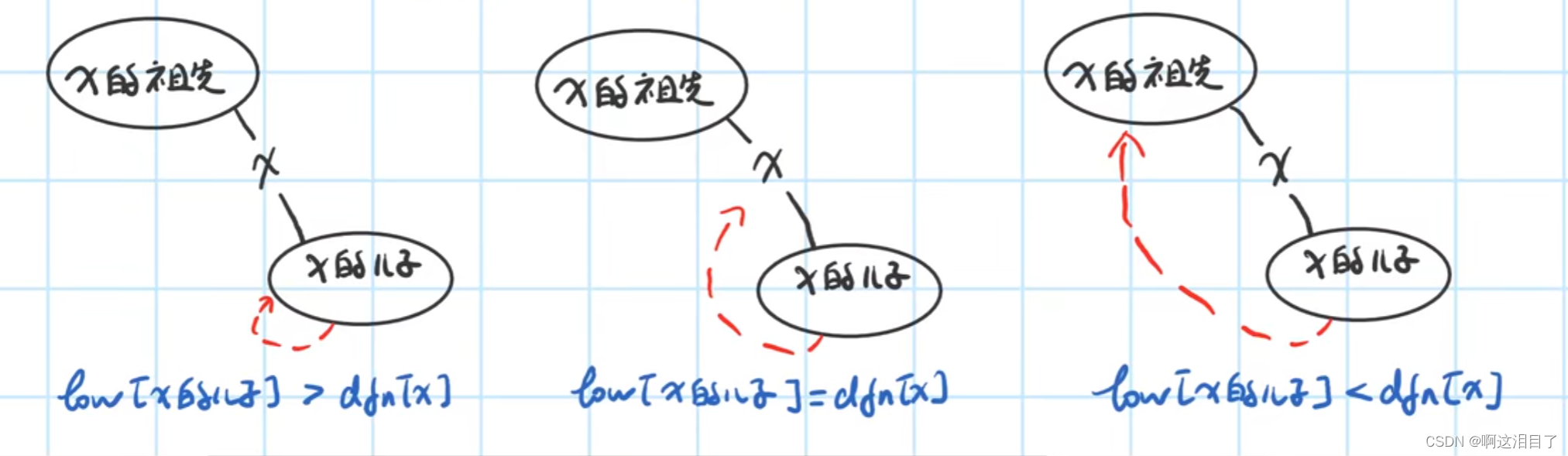
对一个点是否是割点的判断：

如果一个点是割点那么就一定存在两种情况

情况一：这个点不是根节点，且low[x的子节点]>=dfn[x]（x的子节点回溯后的时间仍然大于等于这个节点的时间戳，那么x就是割点）

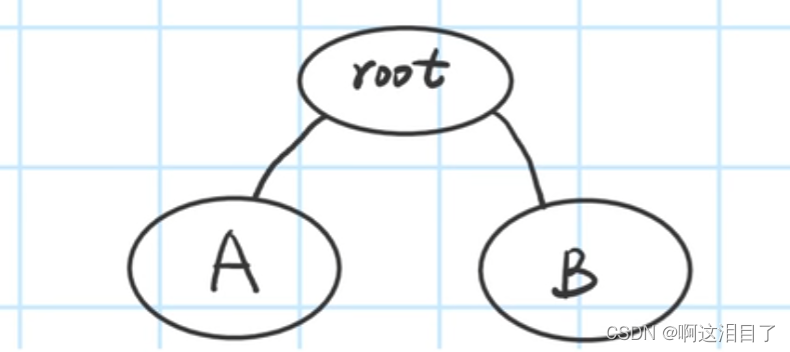
情况二：如果一个点事根节点，且他有至少两个儿子，那这个点也一定是割点

求割边就是:假设x->y是桥，那么low[y]>low[x]

#include <bits/stdc++.h>
using namespace std;const int N=2e5+4;
int head[N],tot,n,m,low[N],dfn[N],s,cut[N];struct	edge{	//链式前向星 int from;	//数值域 int to;int next;	//指针域 
}e[N];void add(int u,int v){	//构造链式前向星 e[++tot].from=u;	//数组下标为tot的位置存放一条边的关系 e[tot].to=v;e[tot].next=head[u];	//由于是链表的头部插入，所以新来的节点，指针指向下一个节点 head[u]=tot;			//头指针变成新来的指针，头指针的下标为当前节点的下标，意味着以u为比编号的链表的头是tot 
}void tarjan(int u,int fa){	//tarjan算法求割点 dfn[u]=low[u]=++s;	//dfn记录时间戳，low记录最小回溯时间 int child=0;	//记录子树数量 for (int i=head[u];i;i=e[i].next){	//遍历当前节点的所有邻居节点 int v=e[i].to;if (!dfn[v]){	//如果没有被访问过，那么就继续深度搜索 tarjan(v,fa);	low[u]=min(low[u],low[v]);	//子节点更新后，也需要更新父节点 //割点有两种，一种：是父亲节点且有大于等于两个的子树,第二中是，子节点回溯最短时间大于当前时间戳if (low[v]>=dfn[u] && u!=fa){	 cut[u]=1;}if (u==fa) child++;}low[u]=min(low[u],dfn[v]);	//如果u的邻居节点v已经访问过了，那么就表示v比u更早被访问，所以需要更新u节点 }if (u==fa && child>=2){cut[u]=1;}
}int main(){int cnt=0;cin>>n>>m;for (int i=1;i<=m;++i){int u,v;cin>>u>>v;add(u,v);add(v,u);}for (int i=1;i<=n;++i){if (!dfn[i]) tarjan(i,i);}for (int i=1;i<=n;++i){if (cut[i]) cnt++;}cout<<cnt<<endl;for (int i=1;i<=n;++i){if (cut[i]) cout<<i<<" ";}
}

受欢迎的牛 Ghttps://www.luogu.com.cn/problem/P2341

题目描述

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 �A 喜欢 �B，�B 喜欢 �C，那么 �A 也喜欢 �C。牛栏里共有 �N 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

输入格式

第一行：两个用空格分开的整数：�N 和 �M。

接下来 �M 行：每行两个用空格分开的整数：�A 和 �B，表示 �A 喜欢 �B。

输出格式

一行单独一个整数，表示明星奶牛的数量。

输入输出样例

输入 #1复制

3 3
1 2
2 1
2 3

输出 #1复制

1

说明/提示

只有 33 号奶牛可以做明星。

【数据范围】

对于 10%10% 的数据，�≤20N≤20，�≤50M≤50。

对于 30%30% 的数据，�≤103N≤103，�≤2×104M≤2×104。

对于 70%70% 的数据，�≤5×103N≤5×103，�≤5×104M≤5×104。

对于 100%100% 的数据，1≤�≤1041≤N≤104，1≤�≤5×1041≤M≤5×104。

#include <bits/stdc++.h>
using namespace std;const int N=5e4+5;struct edge{int from;int to;int next;
}e[N];int n,m,head[N],dfn[N],low[N],tot,color[N],num[N],out[N],s,instack[N],id;
stack<int>st;void add(int u,int v){	e[++tot].from=u;e[tot].to=v;e[tot].next=head[u];head[u]=tot;
}void tarjan(int u){	//tarjan缩点法 ,和割点法的区别在于多了栈，染色数组 dfn[u]=low[u]=++s;st.push(u);instack[u]=1;for (int i=head[u];i;i=e[i].next){int v=e[i].to;if (!dfn[v]){tarjan(v);low[u]=min(low[u],low[v]);}else if (instack[v]){low[u]=min(low[u],low[v]);}}if (dfn[u]==low[u]){id++;while (st.top()!=u){color[st.top()]=id;		//一个SCC里面的编号，染同样的颜色 num[id]++;instack[st.top()]=0;st.pop();}color[st.top()]=id;num[id]++;instack[st.top()]=0;st.pop();}
}int main(){cin>>n>>m;for (int i=1;i<=m;++i){int u,v;cin>>u>>v;add(u,v);}for (int i=1;i<=n;++i){if(!dfn[i]){tarjan(i);}}for (int i=1;i<=n;++i){for (int j=head[i];j;j=e[j].next){if (color[i] != color[e[j].to]){out[color[i]]++;}}}int ans=0;for (int i=1;i<=id;++i){if (out[i]==0){if (ans){cout<<0;return 0;}ans=i;}}cout<<num[ans];
}

拓扑排序https://www.luogu.com.cn/problem/B3644

题目描述

有个人的家族很大，辈分关系很混乱，请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列，使得每个人的后辈都比那个人后列出。

输入格式

第 11 行一个整数 �N（1≤�≤1001≤N≤100），表示家族的人数。接下来 �N 行，第 �i 行描述第 �i 个人的后代编号 ��,�ai,j，表示 ��,�ai,j 是 �i 的后代。每行最后是 00 表示描述完毕。

输出格式

输出一个序列，使得每个人的后辈都比那个人后列出。如果有多种不同的序列，输出任意一种即可。

输入输出样例

输入 #1复制

5
0
4 5 1 0
1 0
5 3 0
3 0

输出 #1复制

2 4 5 3 1

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3fconst int N=105;struct edge{int from;int to;int next;
}e[N];int head[N],tot,n,in[N];void add(int u,int v){e[++tot].from=u;e[tot].to=v;e[tot].next=head[u];head[u]=tot;
}void topo(){queue<int>q;for (int i=1;i<=n;++i){		//入度为0的节点输出并入队 if (!in[i]) cout<<i<<" ",q.push(i);}while (!q.empty()){int x=q.front(); q.pop();for (int i=head[x];i;i=e[i].next){in[e[i].to]--;	//出队后，相邻节点的入度就减1 if (!in[e[i].to]){	//如果入度为0，就输出并入队 cout<<e[i].to<<" ";q.push(e[i].to);}}}
}signed main(){cin>>n;for (int i=1;i<=n;++i){int m;while (true){cin>>m;if (!m) break;add(i,m);in[m]++;	//长辈指向后辈,但后辈不能指向长辈,后辈的入度+1 }}topo();
}

刷题：

堆https://www.luogu.com.cn/problem/P3378

题目描述

给定一个数列，初始为空，请支持下面三种操作：

给定一个整数 �x，请将 �x 加入到数列中。

输出数列中最小的数。

删除数列中最小的数（如果有多个数最小，只删除 11 个）。

输入格式

第一行是一个整数，表示操作的次数 �n。
接下来 �n 行，每行表示一次操作。每行首先有一个整数 ��op 表示操作类型。

若 ��=1op=1，则后面有一个整数 �x，表示要将 �x 加入数列。

若 ��=2op=2，则表示要求输出数列中的最小数。

若 ��=3op=3，则表示删除数列中的最小数。如果有多个数最小，只删除 11 个。

输出格式

对于每个操作 22，输出一行一个整数表示答案。

输入输出样例

输入 #1复制

5
1 2
1 5
2
3
2

输出 #1复制

2
5

说明/提示

【数据规模与约定】

对于 30%30% 的数据，保证 �≤15n≤15。

对于 70%70% 的数据，保证 �≤104n≤104。

对于 100%100% 的数据，保证 1≤�≤1061≤n≤106，1≤�<2311≤x<231，��∈{1,2,3}op∈{1,2,3}。

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3fconst int N=1e6+5;int op,n;
priority_queue<int,vector<int>,greater<int> >q;signed main(){cin>>n;while (n--){cin>>op;if (op==1){int x; cin>>x;q.push(x);}else if (op==2){cout<<q.top()<<endl;}else if (op==3){q.pop();}}
}

黑匣子https://www.luogu.com.cn/problem/P1801

题目描述

Black Box 是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量 �i。最开始的时候 Black Box 是空的．而 �=0i=0。这个 Black Box 要处理一串命令。

命令只有两种：

ADD(x)：把 �x 元素放进 Black Box;

GET：�i 加 11，然后输出 Black Box 中第 �i 小的数。

记住：第 �i 小的数，就是 Black Box 里的数的按从小到大的顺序排序后的第 �i 个元素。

我们来演示一下一个有11个命令的命令串。（如下表所示）

序号

操作

�i

数据库

输出

1

ADD(3)

00

33

/

2

GET

11

33

33

3

ADD(1)

11

1,31,3

/

4

GET

22

1,31,3

33

5

ADD(-4)

22

−4,1,3−4,1,3

/

6

ADD(2)

22

−4,1,2,3−4,1,2,3

/

7

ADD(8)

22

−4,1,2,3,8−4,1,2,3,8

/

8

ADD(-1000)

22

−1000,−4,1,2,3,8−1000,−4,1,2,3,8

/

9

GET

33

−1000,−4,1,2,3,8−1000,−4,1,2,3,8

11

10

GET

44

−1000,−4,1,2,3,8−1000,−4,1,2,3,8

22

11

ADD(2)

44

−1000,−4,1,2,2,3,8−1000,−4,1,2,2,3,8

/

现在要求找出对于给定的命令串的最好的处理方法。ADD 命令共有 �m 个，GET 命令共有 �n 个。现在用两个整数数组来表示命令串：

�1,�2,⋯ ,��a1,a2,⋯,am：一串将要被放进 Black Box 的元素。例如上面的例子中 �=[3,1,−4,2,8,−1000,2]a=[3,1,−4,2,8,−1000,2]。

�1,�2,⋯ ,��u1,u2,⋯,un：表示第 ��ui 个元素被放进了 Black Box 里后就出现一个 GET 命令。例如上面的例子中 �=[1,2,6,6]u=[1,2,6,6] 。输入数据不用判错。

输入格式

第一行两个整数 �m 和 �n，表示元素的个数和 GET 命令的个数。

第二行共 �m 个整数，从左至右第 �i 个整数为 ��ai，用空格隔开。

第三行共 �n 个整数，从左至右第 �i 个整数为 ��ui，用空格隔开。

输出格式

输出 Black Box 根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入 #1复制

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出 #1复制

3
3
1
2

说明/提示

数据规模与约定

对于 30%30% 的数据，1≤�,�≤1041≤n,m≤104。

对于 50%50% 的数据，1≤�,�≤1051≤n,m≤105。

对于 100%100% 的数据，1≤�,�≤2×105,∣��∣≤2×1091≤n,m≤2×105,∣ai∣≤2×109，保证 �u 序列单调不降。

序号	操作	�i	数据库	输出
1	`ADD(3)`	00	33	/
2	`GET`	11	33	33
3	`ADD(1)`	11	1,31,3	/
4	`GET`	22	1,31,3	33
5	`ADD(-4)`	22	−4,1,3−4,1,3	/
6	`ADD(2)`	22	−4,1,2,3−4,1,2,3	/
7	`ADD(8)`	22	−4,1,2,3,8−4,1,2,3,8	/
8	`ADD(-1000)`	22	−1000,−4,1,2,3,8−1000,−4,1,2,3,8	/
9	`GET`	33	−1000,−4,1,2,3,8−1000,−4,1,2,3,8	11
10	`GET`	44	−1000,−4,1,2,3,8−1000,−4,1,2,3,8	22
11	`ADD(2)`	44	−1000,−4,1,2,2,3,8−1000,−4,1,2,2,3,8	/

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int long long
#define INF 0x3f3f3f3f3f3f3f3fconst int N=2e5+5;int a[N],u[N],m,n,s,k;priority_queue<int>q1;
priority_queue<int,vector<int>,greater<int> >q2;signed main(){cin>>n>>m;k=1;for (int i=1;i<=n;++i){cin>>a[i];}for (int i=1;i<=m;++i){cin>>u[i];}for (int i=1;i<=n;++i){q1.push(a[i]);if (q1.size()>s){q2.push(q1.top());q1.pop();}while (u[k]==i){s++;cout<<q2.top()<<endl;q1.push(q2.top());q2.pop();k++;}}
}

这篇关于2.18学习总结的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！