Leetcode3026. 最大好子数组和

本文主要是介绍Leetcode3026. 最大好子数组和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Every day a Leetcode

题目来源：3026. 最大好子数组和

解法1：哈希 + 前缀和

哈希表 hash = unordered_map<int, vector<long long>> 存储数组 nums 的元素 x 及其到 x 为止的前缀和 preSum。

遍历数组 nums，设当前元素为 x，前缀和为 sum：

1. 在哈希表中寻找键 x + k，若找到，更新答案 ans = max(ans, sum + x - *min_element(it->second.begin(), it->second.end()))；
2. 在哈希表中寻找键 x - k，若找到，更新答案 ans = max(ans, sum + x - *min_element(it->second.begin(), it->second.end()))；
3. 向哈希表中插入 hash[x].push_back(sum)；
4. 更新前缀和 sum += x。

最后返回答案。

代码：

/** @lc app=leetcode.cn id=3026 lang=cpp** [3026] 最大好子数组和*/// @lc code=start
class Solution
{
public:long long maximumSubarraySum(vector<int> &nums, int k){long long ans = LLONG_MIN, sum = 0;unordered_map<int, vector<long long>> hash;for (int &x : nums){auto it = hash.find(x + k);if (it != hash.end())ans = max(ans, sum + x - *min_element(it->second.begin(), it->second.end()));it = hash.find(x - k);if (it != hash.end())ans = max(ans, sum + x - *min_element(it->second.begin(), it->second.end()));hash[x].push_back(sum);sum += x;}return ans == LLONG_MIN ? 0 : ans;}
};
// @lc code=end

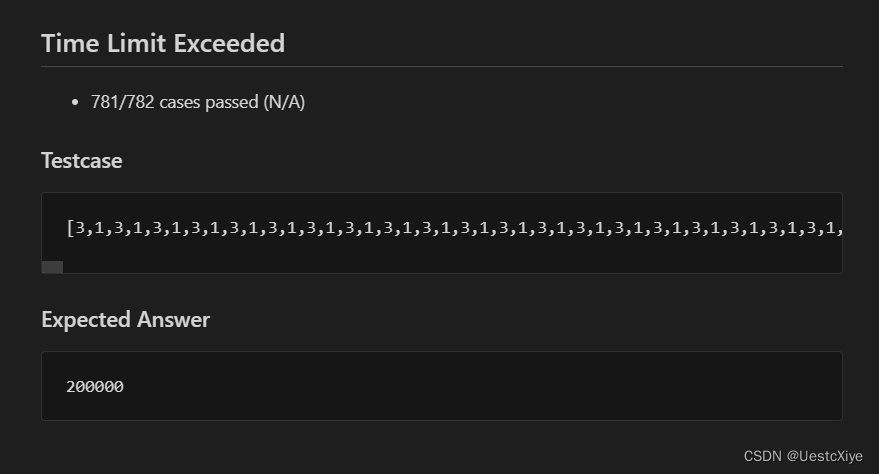
结果：

超时。

复杂度分析：

时间复杂度：O(n)，其中 n 是数组 nums 的元素个数。

空间复杂度：O(n)，其中 n 是数组 nums 的元素个数。

优化

我们发现，哈希表中最需要存储元素 x 及其对应的最小的前缀和，这样算出来的子数组元素总和是最大的。

修改：

1. 更新答案 ans = max(ans, sum + x - it->second)；
2. 每次还有在哈希表中查找 x，如果找不出或者当前前缀和 sum 小于 hash[x]，更新 hash[x] = sum。

代码：

/** @lc app=leetcode.cn id=3026 lang=cpp** [3026] 最大好子数组和*/// @lc code=start
class Solution
{
public:long long maximumSubarraySum(vector<int> &nums, int k){long long ans = LLONG_MIN, sum = 0;unordered_map<int, long long> hash;for (int &x : nums){auto it = hash.find(x + k);if (it != hash.end())ans = max(ans, sum + x - it->second);it = hash.find(x - k);if (it != hash.end())ans = max(ans, sum + x - it->second);it = hash.find(x);if (it == hash.end() || sum < it->second)hash[x] = sum;sum += x;}return ans == LLONG_MIN ? 0 : ans;}
};
// @lc code=end

结果：

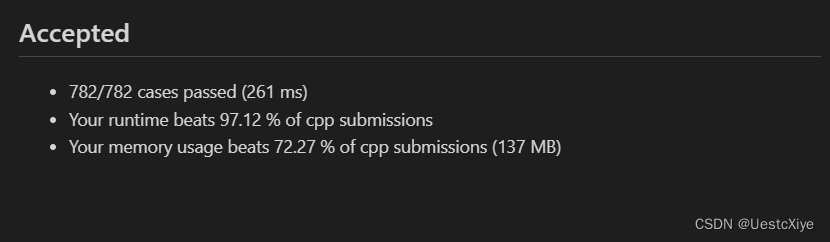
复杂度分析：

时间复杂度：O(n)，其中 n 是数组 nums 的元素个数。

空间复杂度：O(n)，其中 n 是数组 nums 的元素个数。

这篇关于Leetcode3026. 最大好子数组和的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---