D - Doin‘ Time

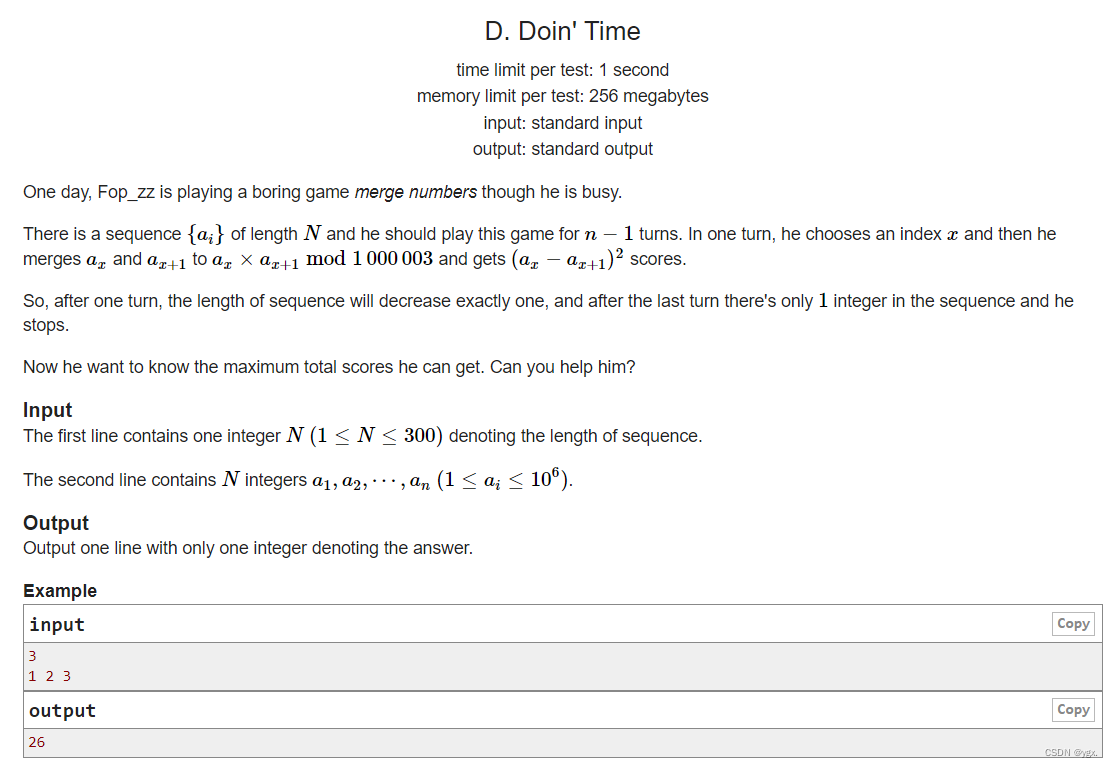
该题考的是区间DP问题

可以把题中所说的选中x把a[x]用a[x]*a[x+1]%P替换理解为将a[x],a[x+1]合并得到a[x]*a[x+1]%P

 f[l][r]表示将 a[l] ~a[r] 合并的所有不同方法的集合 属性为得分的max

状态转移方程 f[l][r] = f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+(a[l][k]-a[k+1][r])*(a[l][k]-a[k+1][r]));

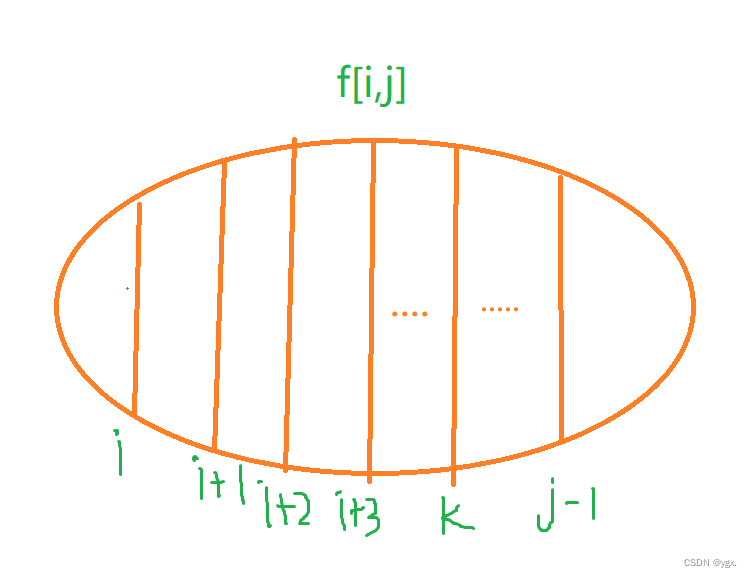
f[i,j] 可以以最后 一次合并的分界不同将其分为上图的小份(k表示,前面先把a[i~~k]合并成一堆,再把a[+1~~j]合并成一堆,最后一次合并是合并了a[i,k],和a[k+1,r])

那么f[l,r]可以这样算

			f[l][r]=-0x3f3f3f3f;for(int k=l;k<r;k++){f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+(b[l][k]-b[k+1][r])*(b[l][k]-b[k+1][r]));}

b[i,j]表示把a[i~j]合并之后得到的新的数

	for(int i=1;i<=n;i++){long long t=1;for(int j=i;j<=n;j++) //状态转移方程中可以看出需要用到b[i,i],故二层循环这么写{t = t * num[j] % p;b[i][j] = t;}}

AC代码

#include<bits/stdc++.h>
using namespace std;const int N=310,p=1000003;
long long f[N][N],b[N][N];
int a[N];int main()
{int n;scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++){long long t=1;for(int j=i;j<=n;j++){t = t * a[j] % p;b[i][j] = t;}}for(int len=2;len<=n;len ++){for(int i=1;len+i-1<=n;i++){int l = i, r = len+i-1;f[l][r]=-0x3f3f3f3f;for(int k=l;k<r;k++){f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+(b[l][k]-b[k+1][r])*(b[l][k]-b[k+1][r]));}}}printf("%lld\n",f[1][n]);return 0;
}