本文主要是介绍《剑指 Offer》专项突破版 - 面试题 45 和 46 : 二叉树最低层最左边的值和二叉树的右侧视图(C++ 实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
面试题 45 : 二叉树最低层最左边的值
面试题 46 : 二叉树的右侧视图
面试题 45 : 二叉树最低层最左边的值
题目:
如何在一棵二叉树中找出它最低层最左边节点的值?假设二叉树中最少有一个节点。例如,在下图所示的二叉树中最低层最左边一个节点的值是 5。
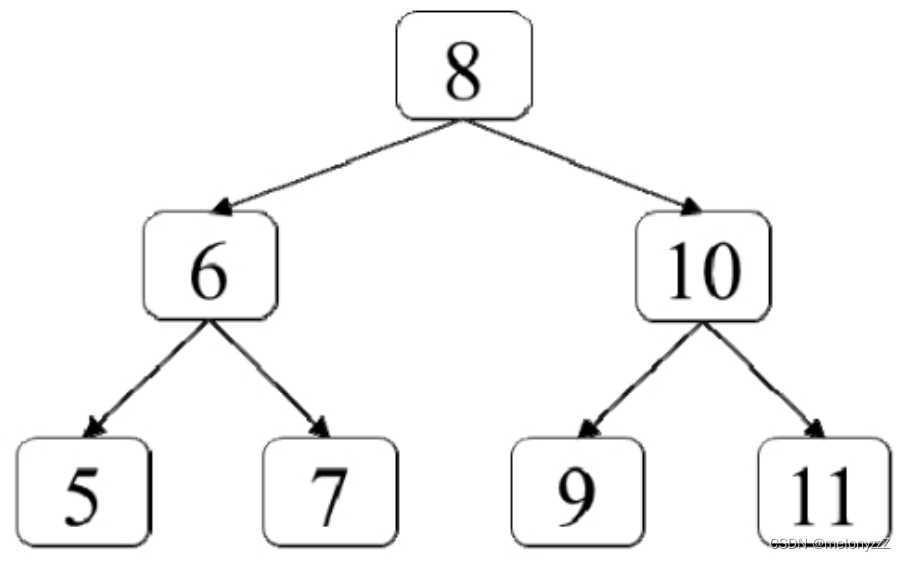
分析:
这是一个关于二叉树的问题,而且还与二叉树的层相关,因此基本可以确定这个题目是在考查二叉树的广度优先搜索。通常,广度优先搜索算法是从上到下遍历二叉树的每一层,并且从左到右遍历同一层中的每个节点。位于某一层最左边的节点就是该层中第 1 个遍历到的节点,最低层最左边的节点就是最后一层的第 1 个节点。
可以用一个变量 bottomLeft 来保存每一层最左边的节点值。在遍历二叉树时,每当遇到新的一层时就将变量 bottomLeft 的值更新为该层第 1 个节点的值。当整棵二叉树都被遍历完之后,变量 bottomLeft 的值就是最后一次更新的值,也就是最后一层的第 1 个节点的值。
代码实现:
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> q;q.push(root); // 二叉树中最少有一个节点int curLevelSize = 1;int bottomLeft = root->val;while (curLevelSize){while (curLevelSize--){TreeNode* front = q.front();q.pop();if (front->left)q.push(front->left);if (front->right)q.push(front->right);}curLevelSize = q.size();if (curLevelSize != 0)bottomLeft = q.front()->val;}return bottomLeft;}
};面试题 46 : 二叉树的右侧视图
题目:
给定一棵二叉树,如果站在该二叉树的右侧,那么从上到下看到的节点构成二叉树的右侧视图。例如,下图中二叉树的右侧视图包含节点 8、节点 10 和节点 7。请写一个函数返回二叉树的右侧视图节点的值。
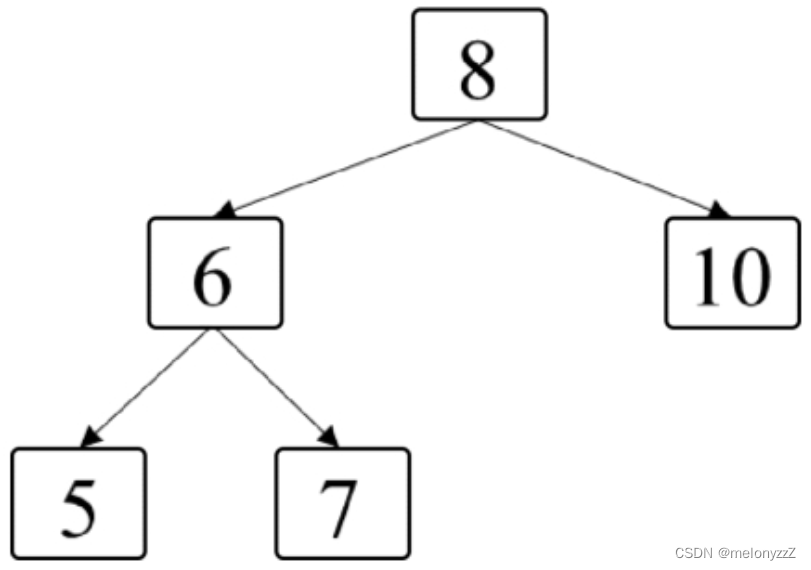
分析:
这个题目提出了一个新概念,即二叉树的右侧视图。当站在二叉树的右侧时,看到的应该是每层最右边的一个节点,而每层的其他节点都被最右边的节点挡住。因此,二叉树的右侧视图其实就是从上到下每层最右边的节点。
代码实现:
class Solution {
public:vector<int> rightSideView(TreeNode* root) {vector<int> result;if (root == nullptr)return result;queue<TreeNode*> q;q.push(root);int curLevelSize = 1;while (curLevelSize){while (curLevelSize--){TreeNode* front = q.front();q.pop();if (curLevelSize == 0)result.push_back(front->val);
if (front->left)q.push(front->left);
if (front->right)q.push(front->right);}curLevelSize = q.size();}return result;}
};这篇关于《剑指 Offer》专项突破版 - 面试题 45 和 46 : 二叉树最低层最左边的值和二叉树的右侧视图(C++ 实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






