本文主要是介绍hdu-1358 KMP,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
思路
题目意思简单来说就是给定字符串,求该字符串的最小周期长度。
关于周期
符号约定:t表示一个周期,kt表示k个周期构成的字符串,即tttttt…t,共k个t,k代表周期数,‘+’表示连接字符串
- 每个前缀至少可以看成一个周期
- 我们首先找到的必然是形如2t的周期数大于1的前缀
- 若字符串s=kt+t,则s的周期也为t,周期为(k+1)(看起来是废话)
- 结合 (2)(3),可以归纳出我们通过kt+t的方式找到的周期字符串的周期长度是最小的。
结合kmp来看: - 若s为周期字符串,周期数k>1,则s=(k-1)t+t=t+(k-1)t。因此有结论,若字符串存在长为(k-1)t的最长前后缀匹配,且剩余部分恰好是一个周期长度,则,字符串是一个周期为k的周期字符串,简单证明如下:
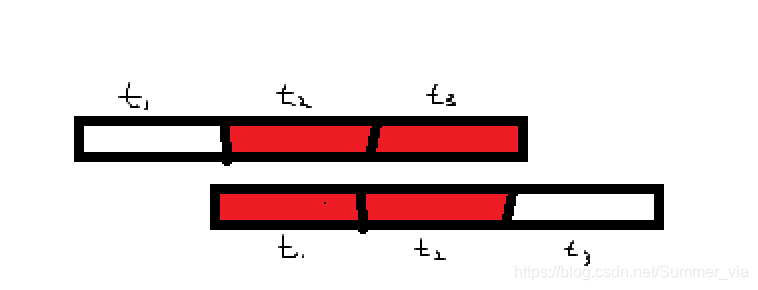
显然,红色部分匹配可知,t1=t2=t3,即该字符串也是周期为t的字符串。
解法
有了如上结论就好求解了。
- 先使用kmp预处理字符串,求出所有最长前后缀匹配。
- 根据上一步结果若某前缀的最长前后缀匹配满足上述结论的条件的话,则可求出该前缀的最小周期。
- 最后根据题目要求输出就可以了
代码实现(c++)
#include<stdio.h>
#include<string.h>
int nxt[1000005];
char str[1000005];
int tt[1000005];
int n;
void kmp_pre(char *s,int l)
{nxt[0]=-1;int i=-1,j=0;while(j<l){while(i!=-1&&s[i]!=s[j]) i =nxt[i];nxt[++j]=++i;}
}
int main()
{int t=0;while(~scanf("%d",&n)&&n){getchar();gets(str);kmp_pre(str,n);for(int i=0;i<n;i++){tt[i]=i+1;if(nxt[i+1]!=0&&nxt[i+1]%tt[nxt[i+1]-1]==0&&i+1-nxt[i+1]==tt[nxt[i+1]-1]) tt[i]=tt[nxt[i+1]-1];//这里对应判断条件}printf("Test case #%d\n",++t);for(int i=0;i<n;i++){if((i+1)/tt[i]>1)printf("%d %d\n",i+1,(i+1)/tt[i]);}puts("");}return 0;
}这篇关于hdu-1358 KMP的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



