C语言空间直角坐标与大地坐标的相互转换实验报告

本文主要是介绍C语言空间直角坐标与大地坐标的相互转换实验报告，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

C语言空间直角坐标与大地坐标的相互转换实验报告

---

源代码附文末或见Github:⬇️
直角坐标与大地坐标的相互转化

branch:

• master: 正常读取输入。
• file_read: 从csv文件获取输入。

一、实验名称：空间直角坐标与大地坐标的相互转换

二、实验目的与要求

三、实验内容

1. 已知某点的空间直角坐标（X、Y、Z）， X = 1546823.34，Y = -3879765.13，Z = 4804185.05，椭球参数a= 6378137m，b= 6356752.3141m，采用下式将其转换为大地坐标（L、B）
   

2. 根据1所求的大地坐标（L、B）及大地高H及相同的椭球参数将其转化为空间直角坐标（X、Y、Z），计算式为：

四、试验设备与环境

五、实验步骤

1 && 2 分析和算法设计

公理1 :由于 $LBH$ 和 $XYZ$ 是相同物理量在相同参考系下的不同表示方法，因此在空间直角坐标系上的某点$(XYZ)$，有且只有一个$LBH$在大地坐标系与之对应。

推论1 只要$XYZ$确定，$LBH$的值就只与$XYZ$的取值有关，而与任何其他变量无关。

下面展开讨论：

由方程可知，虽然 $L$ 可以直接求解，但求 $B$ 的方程中，包含 $B$ 本身，为了验证方程(2)是否可以求解，我们先将方程(2)化简：
$$\begin{array}{c}B=\arctan \frac{Z+N{e}^2\sin B}{\sqrt{X^2+Y^2}}\\ \tan B=\frac{Z+N{e}^2\sin B}{\sqrt{X^2+Y^2}}\end{array}\text{\hspace{1em}(2)}$$
为了方便化简，我们令
$$\sqrt{X^2+Y^2}=R\text{\hspace{1em}(3)}$$
又由于
$$N=\frac{a}{\sqrt{1-e^2{\sin }^{2}B}}\text{\hspace{1em}(4)}$$
将（4）、（3）带入(2)中
$$\begin{array}{cc}\tan B& =\frac{Z}{R}+\frac{e^2}{R}NsinB\\ & =\frac{Z}{R}+\frac{e^2}{R}\frac{\sin B}{\sqrt{1-e^2{\sin }^{2}B}}\\ & =\frac{Z}{R}+\frac{a{e}^2}{R}\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}\end{array}\text{\hspace{1em}(5)}$$
由 推论1 可知，上式中 $\frac{Z}{R}$ 与 $\frac{a{e}^2}{R}$ 与 $B$ 的值无关，为了方便表示，我们令
$$\frac{Z}{R}=C,\frac{a{e}^2}{R}=K.$$

上式化简为：

$$\tan B=K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C\text{\hspace{1em}(6*)}$$

在上式中，由于 $\frac{\tan B}{\sin B}=\cos B$ 不为常量，故无法找到一组$k_1,k_2\in R$ 满足$k_1\tan B+k_2\sin B=0$。因此上式左右两端含有变量 $B$ 的因子是非线性相关的，所以不可以直接通过方程求解。

由此，为得到$B$ 的值，必须通过其他方式求解。

利用计算机程序可以通过不断猜测 $B$ 的值，带入(6)式中，如果(6)左右两端的值足够接近，且由 推论1, 此时猜测到的值 $B_{猜}$ 必然也会接近实际的值$B_{实}$。

我们将上述求 $B$ 的方法称为遍历法，接下来我们设计遍历法的算法。

遍历法

由题设条件，可知$B\in (-\frac{\pi }{2},\frac{\pi }{2})$。

• 一个可执行的算法必须由有限步构成。

但是可能出现的 $B$ 的值确是无限的，为此，我们将 $B$ 进行离散化 ，即每隔很小的值 $\delta (delta)$ ，取一个新的值$B$。

为了方便表示，我们设计损失函数$Loss$用来计算方程左右两端的差值。
$$Loss(B)=\tan B-K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C\text{\hspace{1em}(7)}$$
当函数Loss的值很小时，则认为此时的$B$达到了目标值$B_{实}$。

用数学语言可以描述为：

若取一个足够小的 $\epsilon >0$，

对于
$$B_0=-\frac{\pi }{2}+k\delta ,且(k\in N^{\ast })B_0<\frac{\pi }{2}$$
时，如果满足
$$|Loss(B_0)|<\epsilon$$
则认为 $B=B_0$。

---

梯度下降法

使用遍历法​求解时，往往会由于需要遍历的变量的数量太多，导致程序的运行时间太长，难以得到正确的结果。当我们遍历时，只是盲目的遍历，我们并不知道到底经过多少个 $\delta$ 后，能够使$Loss$函数的绝对值变小。这是因为，我们只用 $Loss$ 函数的值与0比较，这样的比较获得的信息量是十分少的，为了从 $Loss$ 函数中获取更多信息，我们可以考虑将 $Loss$ 函数的绝对值进行求导，将其导函数记为$Los{s}^{\prime }$

我们的目标是使 $Loss$ 函数的值趋近于0，对于一个点$(B,Loss(B))$ ，如果$Loss(B)>0$，我们应该调整 $B$ 的值，使得$Loss(B)$减少，相反，如果$Loss(B)<0$， 我们应该调整$B$的值，使$Loss(B)$增加。

即：

• $Loss(B)>0$, $B$ 向 $Los{s}^{\prime }(B)<0$的方向移动。
• $Loss(B)<0,B$ 向 $Los{s}^{\prime }(B)>0$ 的方向移动。

以点$X=-2758534,Y=-4132154,Z=3986124$为例，

绘制出$Loss$函数的图像：

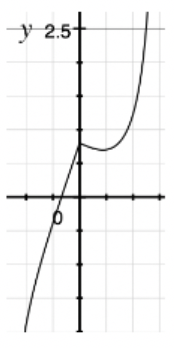
发现$Loss$函数并不是简单的单调函数，用上述算法有可能达到一个使$Loss(B)$为0的点，也有可能达到函数的一个极值点，并不是在所有情况下都能符合条件。

---

二分法

虽然梯度下降法无法实现，但这给我们进一步实现程序提供了思路，即让 $B$ 的取值变得更加具有方向性。

由于当$B\to -\frac{\pi }{2}$ 时，
$$Loss(B)\to -\infty$$
当$B\to \frac{\pi }{2}$时，
$$Loss(B)\to +\infty$$
又由推论2可知，在区间$(-\frac{\pi }{2},\frac{\pi }{2}）$内，$Loss(B)$有且只有一个一个零点。可以很容易想到二分法的求解方式：

• $LoopStart:$
• $mid=\frac{right+left}{2}$
• $ifLoss(mid)>\epsilon ,left=mid$
• $elseifLoss(mid)<-\epsilon ,right=mid$
• $elseB=mid$
• $:LoopEnd$

---

迭代法

由于式(6)
$$\tan B=K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C\text{\hspace{1em}(6*)}$$
如果我们令方程左边的$B=B_{n+1}$ 方程右边的 $B=B_n$，就可以得到一个关于$B$ 的迭代方程。
$$B_{n+1}=\arctan \left(K\frac{1}{\sqrt{\frac{1}{{\sin }^2{B}_n}}-e^2}+C\right)\text{\hspace{1em}(8*)}$$
我们称上面的递推式为函数$Forward(B)$。

以点$X=-2758534,Y=-4132154,Z=3986124$为例，

绘制出$Forward$函数的图像：

上图中粗线为$Forward$函数，虚线为直线 $B_{n+1}=B_n$。

设曲线$Forward$ 与 直线$B_{n+1}=B_n$的交点为 $A$ ，$A$的横坐标为$x_0$，很显然 $A$是函数$Forward$ 的一阶不动点。由递推函数的性质可知，

• 当$B_n<x_0$ 时， $B_{n+1}>B_n$

• 当$B_n>x_0$时，$B_{n+1}<B_n$

• 当$B_n=x_0$时，$B_{n+1}=B_n$

  因此如果迭代次数无穷大，那么$B_n$的值会无限接近于$x_0$或等于$x_0$。

  我们用$Python$模拟一下迭代过程：

  from math import *
  import matplotlib.pyplot as plta = 6378137
  b = 6356752
  e = sqrt((a * a - b * b) / (a * a))
  X = -2758534
  Y = -4132154
  Z = 3986124
  R = sqrt(X * X + Y * Y)
  K = a * e * e / R
  C = Z / R
  x = []
  y = []def forWard(x):N = a / sqrt(1 - e * e * sin(B) * sin(B))tmp = sqrt(1/(sin(x) * sin(x)) - e * e)return atan(K / tmp + 0.1) + CB = C
  times = 100
  t = 0
  while True:t += 1nextB = forWard(B)#plt.plot(t, nextB, '+')B = nextBif t >= times:breakx.append(t)y.append(B)
  plt.xlabel("times")
  plt.ylabel("B")
  plt.plot(x, y)
  plt.show()
  

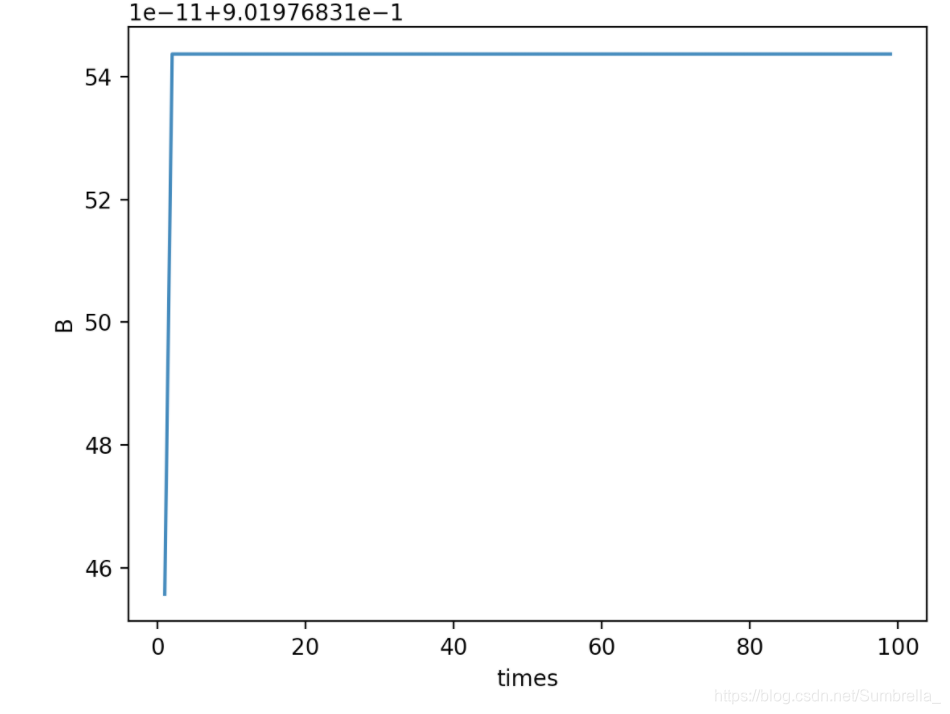
理论和实践都告诉我们，使用迭代公式计算时，$B$ 会趋近于某一个特殊的值$x_0$。

下证：该$x_0$就是我们的目标值$B_{实}$

​ 当 $B=x_0$时，由于 $x_0$是$Forward$ 函数的一阶不动点，故有
$$\tan B=K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C$$
​ 将上式带入$Loss$函数中，可以得到 $Loss(B)=0$，又由推论1知这样的$B$是唯一的，因此$B=x_0$ 就是所求值。

​ 证毕。

(上述证明其实显而易见，用迭代法的关键是证明一阶不动点存在， 但是该证明过程较为复杂，我们可以在物理领域内使用反证法：如果不存在一阶不动点，那么函数$Loss$就没有解，这与实际情况不符，故一定存在一阶不动点)。

第二小问直接带入公式计算。

3流程图

遍历法：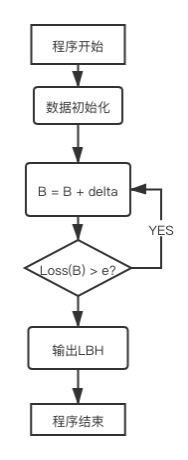

二分法：

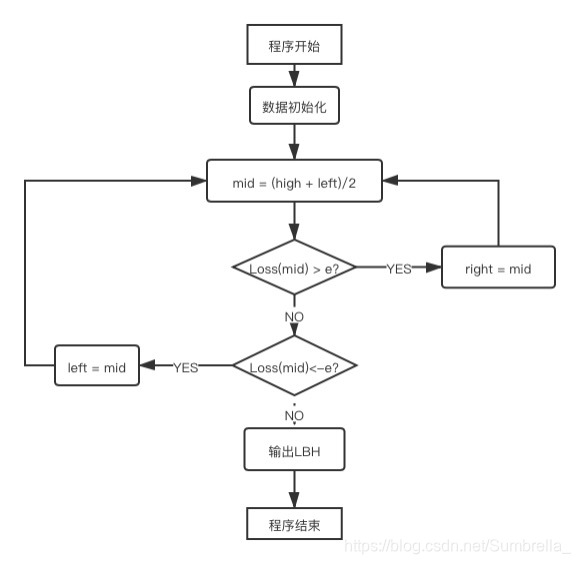
迭代法：

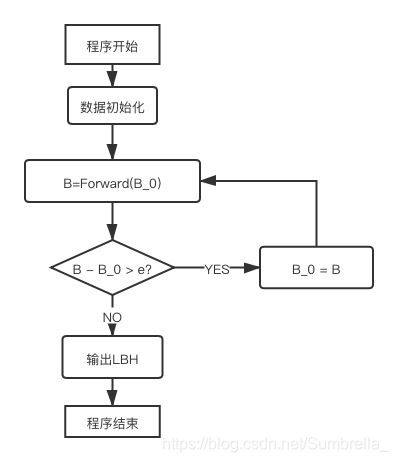
4、 程序代码

本部分只使用迭代法完成代码。

//
//  main.cpp
//  ChangePosition
//
//  Created by Sumbrella on 2020/4/28.
//  Copyright © 2020 Sumbrella All rights reserved.
//
# include <stdio.h>
# include <math.h>typedef long long ll;const ll a = 6378137;
const ll b = 6356752;
const double epslion = 1e-15;
double e, R, K, C;// 配置需要使用的中间参数。
void configure(double X, double Y, double Z)
{e = sqrt((a * a - b * b) / (a * a));R = sqrt(X * X + Y * Y);K = a * e * e / R;C = Z / R;
}// 迭代法迭代一次
double Forward(double B)
{double tmp = sqrt(1 / (sin(B) * sin (B)) - e * e );return atan(K / tmp + C);
}void inputXYZ(double *X,double *Y, double *Z)
{printf("请输入X，Y，Z的值>>>（空格隔开）");scanf("%lf %lf %lf", X, Y, Z);
}void getLBH(double X, double Y, double Z, double *pN, double *pL, double *pB, double *pH)
{double B = C;                   // 让B的初始值为Cwhile (1){double nB = Forward(B);if (nB - B < epslion && nB - B > -epslion)break;B = nB;}double N = a / sqrt(1 - e * e * sin(B) * sin(B));double L = atan2(Y, X);double H = R / cos(B) - N;*pN = N; *pL = L; *pB = B; *pH = H;
}void showLBH(double L, double B, double H)
{printf("转换得到的大地坐标：\n");printf("L = %.3f, B = %.3f, H = %.3f\n", L, B, H);
}void showXYZ(double N, double L, double B, double H)
{double X = (N + H) * cos(B) * cos(L);double Y = (N + H) * cos(B) * sin(L);double Z = (N * (1 - e * e) + H) * sin(B);printf("转换后得到的空间坐标：\n");// printf("N = %.6f", N);printf("X = %.6f, Y = %.6f, Z = %.6f\n", X, Y, Z);
}int main()
{double X, Y, Z;double N, L, B, H;                // 定义变量inputXYZ(&X, &Y, &Z);             // 获取XYZ的值configure(X, Y, Z);               // 配置参数getLBH(X, Y, Z, &N, &L, &B, &H);  // 计算LBH的值showLBH(L, B, H);                 // 输出LBH的值showXYZ(N, L, B, H);              // 输出计算得到的XYZ的值return 0;
}

5、 主要函数和变量说明

主要函数说明见上图。
变量和常量说明：
（X，Y，Z）、（L，B，H）分别对应直角坐标和大地坐标下的坐标值。
C = Z / R， K = ae^2 / R。

6、 程序运行结果

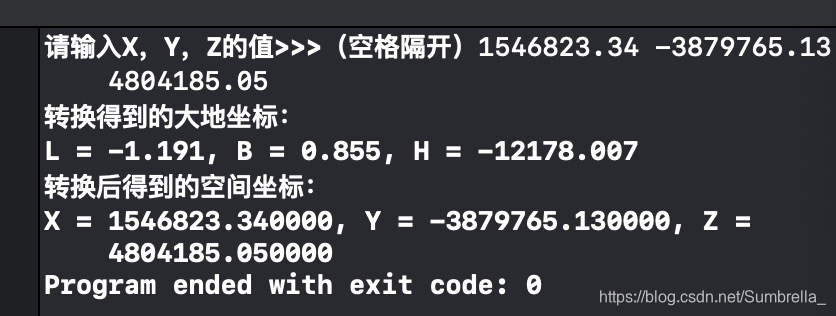
转换后得到的坐标与原始数据完全一致，认为程序通过。

这篇关于C语言空间直角坐标与大地坐标的相互转换实验报告的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---