集成学习概述：三个臭皮匠顶个诸葛亮

本文是《机器学习宝典》第 16篇，读完本文你能够对集成学习有一个简单的认识和理解。

上一篇介绍了面试常考的一个问题：回归决策树，这一篇我们来介绍下集成学习。在生活中，你是不是也会遇到这样的场景：当你对一件事情的判断没有把握的时候，通常会再咨询几个人，听听他们的观点，最后再做出决策。其实这反映出了一个思想：群体决策通常比个体决策更优，用句俗语来说就是：三个臭皮匠顶个诸葛亮。将这个思想应用于机器学习中就是集成学习（ensemble learning）。

为什么集成学习能够提升效果呢

为什么集成学习能够比单模型的效果更好呢？我们从以下几个角度考虑下：

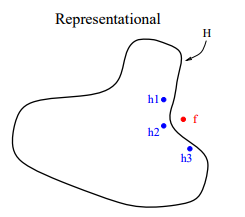
从统计的角度来看，机器学习的任务可用认为是寻找一个最佳的假设空间。在没有充足的数据情况下，学习任务可以找到多个性能差不多的假设空间。如果融合多个模型的预测及过，可以降低预测错误的风险。外面的曲线表示假设空间，内部的曲线表示在训练集上具有不错性能的假设，点 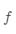表示真实的假设 。我们看到，通过平均这些性能不错的假设，可以得到一个逼近 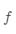的优化假设 。

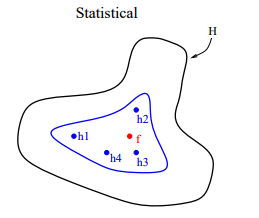
从计算的角度来看，很多优化算法采用局部搜索的方式来寻找最佳参数，这样很容易陷入局部最优解。融合多个模型可以看做是同一个训练集、从不同的起始点进行局部搜索，然后进行结合。这样可以降低陷入局部最优解的风向。

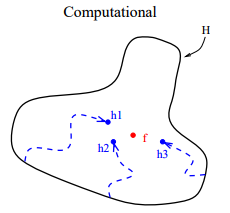
从表示的角度来看，理论上，如果给出足够的训练数据，很多算法可以表示所有的情况，例如神经网络和决策树。但是在很多实际应用中，能够用于训练的数据是有限的。有些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中，此时如果使用单模型肯定无效 。模型融合可以使假设空间扩大，从而使得这些学习任务可能得到正确的表示。

在集成学习中，参与融合的模型叫做基模型，想要使得集成学习的效果好，基模型应该”好而不同“。也就是说，基模型的准确率不能太低，同时基模型之间的多样性（差异性）。

如何增加模型多样性

我们已经知道，增加基模型的多样性能够提高集成学习的效果。一般增加基模型多样性的思路是在学习过程中引入随机性。常见的做法是对数据样本、输入特征、输出结果、算法参数进行扰动。

数据样本扰动

从初始的数据集中产生不同的数据子集，然后利用数据子集训练出不同的基模型。数据样本扰动通常是基于采样法。这种做法简单高效，使用最广。对于不稳定的基学习器（决策树、神经网路等）很有效果，对于一些稳定基学习器（线性学习器、支持向量机、朴素贝叶斯、k近邻算法等）效果不佳。

输入特征扰动

训练样本通常由 一组特征描述 ， 不同的"子空间"提供了观察数据的不同视角 。如果数据包含大量冗余特征， 使用特征扰动会有好处(节省时间 、 多样性提升等);但是若样本数据特征较少或冗余特征很少，则输入特征扰动不适宜使用 。

输出表示扰动

此类做法的基本思路是对输出表示进行操作以增强多样性。如将多分类任务转换为多个二分类任务来训练基模型；“输出调制法”将分类输出转换为回归输出来训练基模型。

算法参数扰动

模型训练一般都需要进行参数调整，比如神经网络的隐藏层结点数、决策树的树深等。这些参数被赋予不同的值可以生成不同的基模型。

其实，我们可以同时采样多种方式来增强模型多样性，比如随机森林同时使用了数据样本扰动和输入特征扰动两种方式。

结合策略

当获得了多个基模型之后，如何将他们组合到一起呢？组合策略主要关注的就是将多个基模型通过某种方式融合后能够提升最后的效果。

假设有 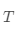个基模型 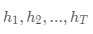，组合后的结果为 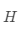，对于回归任务，常见的有两种基础集成策略：简单平均和加权平均。

简单平均是将所有基模型的结果平均后作为集成后的结果：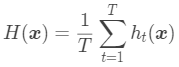

加权平均是说每个基模型的结果权重可以不同，这些权重可以人工制定，也可以从训练数据中学习得到。例如估计出个体学习器的误差，之后令权重大小与误差大小成反比。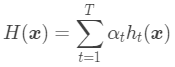

不过由于现实生活中训练样本通常不充分或者存在噪音，这使得学习到的权重不完全可靠。因此，加权平均的效果未必一定优于简单平均效果。一般而言，在个体学习器性能相差较大时宜使用加权平均，而在个体学习器性能相近时宜使用简单平均。

对于分类任务，由于预测的结果可以是类别，也可以是类别概率，对应的可以分为硬投票和软投票。硬投票是采用投票法来融合输出为类别的基模型，软投票则是融合输出为类别概率的基模型。对于硬投票来说，常见的有：绝对多数投票法、 相对多数投票法、加权投票法。对于软投票来说，融合的方式与回归任务中类似，所以这里就主要介绍硬投票相关的融合方式。

绝对投票法是将超过半数基模型预测的类别作为最终的结果，如果有的样本没有那个类别的票数超过了一半，这时候就拒绝预测。

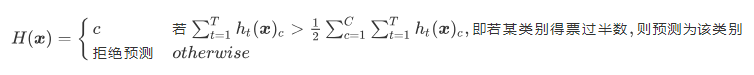
其中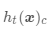表示基模型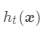在类别 c 上的输出，结果为 1 或 0 。

绝对投票法中会出现“拒绝预测”的情况，如果必须要求提供预测结果，可以考虑使用相对多数投票法。相对多数投票法会将基模型投票次数最多的类别作为最后的输出结果，所以不存在拒绝预测。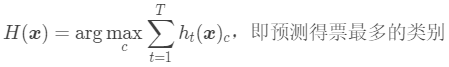

如果基模型的性能差异较大，从直观上来看，让性能更好的模型掌握更多的投票权更合理一些，因此出现了加权投票法。也就是不同的基模型可以有不同的投票权重。

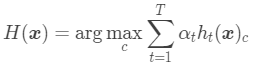
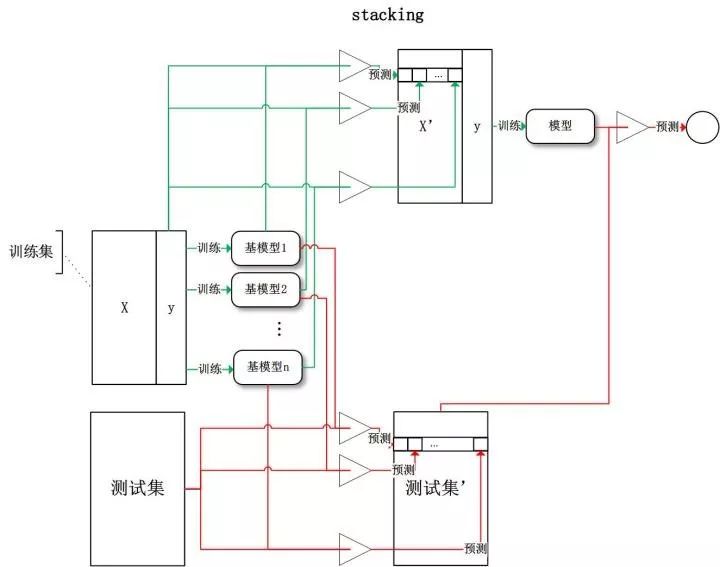
当数据量比较大时，可以通过“学习法”来组合模型，常用的一种叫做 Stacking。Stacking 基于原始数据训练多个基模型，将基模型的输出和原始数据中的目标分别作为新训练集的特征和目标，在新训练集上训练二级模型，将二级模型的输出作为 Stacking 的输出。见下图：

集成算法

除了前面介绍的模型集合策略外，这里介绍两个集成算法：Bagging 和 Boosting 。集成算法更关注的是将基模型经过集成算法来提高模型的泛化能力。

Bagging

Bagging 是的思想是从训练集从进行子抽样组成每个基模型所需要的子训练集，对所有基模型预测的结果进行综合产生最终的预测结果，见下图：

可以看到，需要说明的是，Bagging 采用自助采样法（Bootstrap sampling）进行采样，即对于m个样本的原始训练集，我们每次先随机采集一个样本放入采样集，接着把该样本放回，也就是说下次采样时该样本仍有可能被采集到，这样采集m次，最终可以得到m个样本的采样集。

如果 Bagging 中基学习器都是决策树的话，这时候就属于随机森林算法了，这个之后文章再介绍。

Boosting

与 Bagging 不同的是，Boosting 训练过程为阶梯状，基模型按次序一一进行训练，基模型的训练集按照某种策略每次都进行一定的转化。对所有基模型预测的结果进行线性综合产生最终的预测结果，见下图：

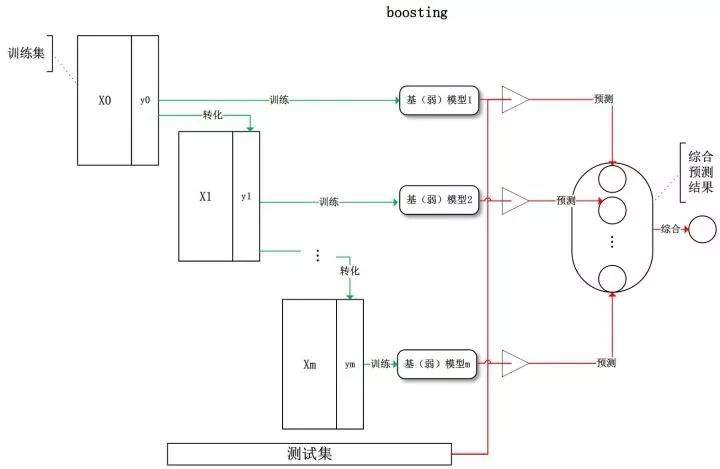
常见的 Boosting 模型有 AdaBoost（Adaptive boosting）算法以及 Gradient Boosting 算法。

Bagging 和 Boosting 的区别

Bagging 可以认为是并行的集成方式，它能够并行的生成相对独立的基模型，Bagging 集成后模型的偏差与基模型近似，但是由于存在多个相对独立的基模型，所以集成后的模型方差会比单个基模型降低。也就是说，Bagging 通过降低方差，提高了模型的泛化能力。

Boosting 可以认为是串行的集成方式，它生成的基模型依赖于前一个基模型，Bagging 集成后模型的方差与基模型近似，但是由于每个基模型都在“纠正”前一个基模型的结果，所以集成后的模型偏差会比单个基模型降低。也就是说，Boosting 通过降低偏差，提高了模型的泛化能力。

参考：

1. 集成学习（ensemble learning）应如何入门？(https://www.zhihu.com/question/29036379/answer/111637662)

2. 独家 |从基础到实现：集成学习综合教程(https://zhuanlan.zhihu.com/p/40485758)

3. 美团机器学习实战

??扫码查看《机器学习宝典》历史内容

（完）

我开通了知识星球，在星球里会分享我个人在数据分析/机器学习/深度学习/推荐系统方面的所学和所得。当前正在星球里分享我录制的机器学习视频课，如果想快速入门和提高自己，可以加入我的星球来交流（加入方式：扫描下方二维码或者点击“阅读原文”）。

人人都是数据分析师，人人都能玩转Pandas | Numpy 精品系列教程汇总 | 我是如何入门机器学习的呢 | 谷歌机器学习43条黄金法则