单精度、半精度之间的转换，及半精度加法实现

本文主要是介绍单精度、半精度之间的转换，及半精度加法实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1位符号位s+8位指数位e+23位尾数位f，共32位，内存占4个字节，表示方式为(-1)^s * 2 ^(e - 127) * 1.f
在这里插入图片描述

1位符号位+5位指数位+10位尾数位，共16位，内存占2个字节，表示方式为(-1)^s * 2 ^(e - 15) * 1.f
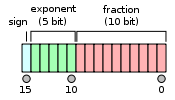
在这里插入图片描述

C语言不包含半精度数据类型，但是只要知道f32在内存中存储占4个字节，f16占两个字节，就可以自己重定义f16数据类型来实现

以3.333333为例，转换为半精度为3.33

将浮点数转换为4字节16进制，依次获取f32符号位，f32指数位，f32尾数位

【实现步骤】

f32符号位:0
f32指数位：1+127 = 128 二进制表示：1000 0000
f32尾数位: 1010 1010 1010 1010 1010 101

f32内存表示为 0 1000 0000 1010 1010 1010 1010 1010 101即0x40555555

获取f16符号位，f16指数位，f16尾数位

【实现步骤】

f16内存表示为 0 10000 1010 1010 10 即0x42aa

转换方式就是单精度转半精度的逆过程
以3.33为例，转换为单精度为3.330000(最后4位随机)

将浮点数转换为2字节16进制，依次获取f16符号位，f16指数位，f16尾数位

【实现步骤】

f16符号位:0
f16指数位：1+15 = 16 二进制表示为:1 0000
f16尾数位: 1010 1010 10

f16内存表示为 0 1 0000 1010 1010 10即0x42aa

获取f32符号位，f32指数位，f32尾数位
【实现步骤】

符号位
符号位保持和单精度一致，3.33为正，f32符号位 = f16符号位 = 0
指数位
f16指数 - 15 = f32指数 - 127 ==>f32指数 = f16指数 - 15 + 127
f32指数= 128，二进制表示为1000 0000
尾数位
10位f16尾数，后面补13个0，补足23位
f32尾数: 1010 1010 1000 0000 000

f32内存表示为 0 1000 0000 1010 1010 1000 0000 000 即0x40554000，从内存读取出来时直接强制转换成float即可
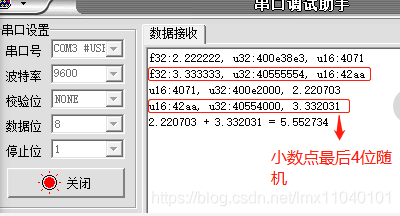
在这里插入图片描述

【注】

尾数决定有效数字的位数，即精度；指数决定范围。因此单精度转换为半精度时会丢失精度，超过半精度范围的单精度转换会溢出，程序中要做好处理（ float尾数位23位，2^23=8.3E6，7位，不同的编译器规定不同，有些是7位，有些8位）
当指数和尾数全为0时，计算机把它看做表示数字0；当指数全为1，尾数全为0时，符号位为0表示正无穷，符号位为1表示负无穷；当指数全为1，尾数不全为0时，无法表示。
因此在用浮点表示时，指数不能全为1或者全为0。float指数位为8位，取值范围为-128 ~ 127,实际使用范围是[-127, 0) && (0, 127];因为指数是以无符号形式存储的，因此指数的偏差为其可能值的一半。对于 float 类型，偏差为 127，f16就是15；存储指数值减去偏差值就是实际二进制科学记数法的指数值。
代码包下载地址
【fp16补充】
正无穷:符号位为0，指数位全为1，尾数位全为0， 0 11111 0000000000
负无穷:符号位为1，指数位全为1，尾数位全为0， 1 11111 0000000000
零(包括正零和负零)：指数，尾数全为0，0 00000 0000000000，1 00000 0000000000
NAN:指数全为1，尾数非全0：0 11111 0000000001（自定义）

【fp16能表示的数据范围】
(-1)^s * 2 ^(e - 15) * 1.f
= (-1)^s * 2 ^(30 - 15) * (1+1-2^-10)
= (-1)^s * 2 ^(15) * (2-2^-10)
= (-1)^s * 32768 * (2-2^-10)
= -65504 ~ 65504

这篇关于单精度、半精度之间的转换，及半精度加法实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！