HDU - 3038 - How Many Answers Are Wrong （带权并查集）

本文主要是介绍HDU - 3038 - How Many Answers Are Wrong （带权并查集），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意：有N个数字，M组关系。每组关系三个数字a,b,s表示a~b的和为s。问与前面产生矛盾的话有几组？

思路：带权并查集。多开一个权值数组，存储到自己和父节点的区间和。

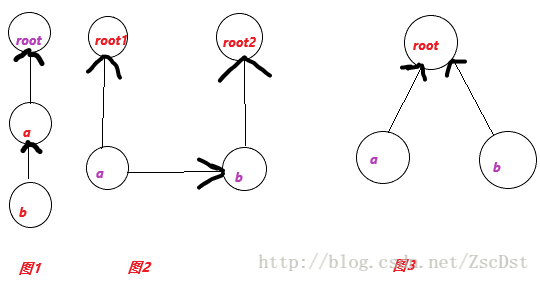
图一：路径压缩，b~root的和 = b~a的和 + a ~ root的和。

图二：合并操作，现在我们知道a~root1和b~root2的区间和，又告诉了我们a~b的区间和，把root2并到root1上的话，

root1~root2的区间和为（a~b）+ (b~root2) - （a~root1）。

图三：求a~b的区间和，a~b的和 = （a~root） - （b ~ root）的和。

[cpp]  view plain copy 
#include<bits/stdc++.h>  
using namespace std;  
const int MAXN = 200005;  
int n, m, ans, f[MAXN], w[MAXN];//并查集数组和关系数组  
//w[i]表示跟根节点的差  
void init()  
{  
    ans = 0;  
    for (int i = 0; i <= n; i++)  
    {  
        f[i] = i; w[i] = 0;  
    }  
}  
int Find(int x)  
{  
    if (f[x] == x) return x;  
    int t = f[x];  
    f[x] = Find(f[x]);  
    w[x] = w[x] + w[t];  
    return f[x];  
}  
void Union(int a, int b, int s)  
{  
    int root1 = Find(a), root2 = Find(b);  
    if (root1 != root2)  
    {  
        f[root1] = root2;  
        w[root1] = w[b] + s - w[a];  
    }  
    else  
    {  
        if (abs(w[a] - w[b]) != s) ans++;  
    }  
}  
int main()  
{  
    while(~scanf("%d%d", &n, &m))  
    {  
        init();//初始化  
        while (m--)  
        {  
            int a, b, s;  
            scanf("%d%d%d", &a, &b, &s);  
            Union(a - 1, b, s);//a~b的区间和为w[b] - w[a - 1]  
        }  
        printf("%d\n", ans);  
    }  
    return 0;  
}  
/* 
10 5 
1 10 100 
7 10 28 
1 3 32 
4 6 41 
6 6 1 
*/  