这篇文章用于记录柏林噪声的一些实践,在开始前,先看下维斯百科里对柏林噪声的一些说明.
用随机法产生的噪声图像和显然自然界物体的随机噪声有很大差别,不够真实。1985年Ken Perlin指出[1],一个理想的噪声应该具有以下性质:
- 对旋转具有统计不变性;
- 能量在频谱上集中于一个窄带,即:图像是连续的,高频分量受限;
- 对变换具有统计不变性。
先来看下一张图:

这二张图都是模仿海波(只是看二者波形,颜色啥的先不要看。。。),同样的模型密度,一张是随机点生成高度的,一张是经过柏林噪声生成的高度。通过二张图的对比,让我们对柏林噪声先有个初步的认识。
查找了一些资料,发现对柏林噪声的定义各有不同,有些定义是柏林噪声是由一系列的Coherent noise构成,而在维基里,定义的是前面的Coherent noise是柏林噪声,而前面的柏林噪声应定义为分形噪声,就是说,分形噪声是由柏林噪声来组成的。在这里,因为大部分文章都采用第一张说法,这里的说明也采用第一种定义。
那面上面的第二张图就是一个Coherent noise(后面直接简称noise)生成的高度点,网上关于noise生成方法很多,有着色器版的,有C语言版的,有改进版的,还有经典版的,好吧,刚开始看完全找不到北,最后下下心来,把Nvidia的一个关于柏林噪声的例子下来,因为想方便追踪一下执行过程,把其中Cg代码改为F#代码。Nvida例子 http://http.download.nvidia.com/developer/SDK/Individual_Samples/samples.html 其中Vertex Noise程序 vnoise地址 。
noise分别有一维,多维,最能说明情况的应该是二维,明白二维nose的生成过程,一维和多维的就很清楚了。先来看下noise的原理,网上讲解的非常多,下面我认为能清楚的一些说明摘抄下来:
首先是维基百科里说的。
经典Perlin噪声[编辑]
Perlin在上述文章中提出了一种产生符合要求的一维噪声函数的简单方法,这是后续工作的基础:
- 在一维坐标轴上,选择等距的无穷个点,将值空间划分为等长的线段(为方便起见,选择坐标值为整数的点),为每个点随机指定一个值和一个梯度(在一维的情况,梯度就是斜率);
- 对于坐标值为整数的点,将该点对应的值作为噪声图像上该点的值;对于坐标值不为整数的点,将相邻两点的值和根据梯度进行插值运算,获得该点的灰度。
插值使用的函数是一个在0处为1,在1处为0,在0.5处为0.5的连续单调减函数。例如,设 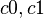 为左右两整数点的颜色,
为左右两整数点的颜色, 为该点距离左边点的距离,使用
为该点距离左边点的距离,使用  作为插值函数,则该点的值为
作为插值函数,则该点的值为 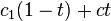 。
。
 是线性插值,得到的结果人工痕迹严重,且在整数点上不连续。Perlin建议使用
是线性插值,得到的结果人工痕迹严重,且在整数点上不连续。Perlin建议使用  作为插值函数 [1],后来又建议使用
作为插值函数 [1],后来又建议使用  作为插值函数[2]。对于二维的情况,可以将上述算法进行推广,即:
作为插值函数[2]。对于二维的情况,可以将上述算法进行推广,即:
- 为所有坐标为
 且
且  都是整数的点指定一个值,同时指定一个梯度,这些点将空间分成方格;
都是整数的点指定一个值,同时指定一个梯度,这些点将空间分成方格; - 对于坐标轴为整数的点,即上述方格的顶点,将为它指定的值作为该点的值;对于某个方格内部的点
 ,用所在方格四个顶点的值和梯度进行插值。
,用所在方格四个顶点的值和梯度进行插值。
例如,对于点  ,令
,令  它所在方格的四个顶点分别为:
它所在方格的四个顶点分别为: 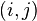 、
、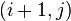 、
、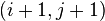 、
、 。令
。令  ,这四个顶点对点
,这四个顶点对点  的贡献可以用它们的梯度(
的贡献可以用它们的梯度( )和
)和  点与这四个顶点的方向(
点与这四个顶点的方向( 、
、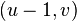 、
、 、
、 )进行点积获得。但是在二维的情况下,插值更为复杂。首先需要对
)进行点积获得。但是在二维的情况下,插值更为复杂。首先需要对 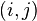 和
和 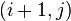 两点在
两点在  方向插值,得到点
方向插值,得到点 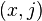 的值;之后对
的值;之后对  和
和 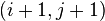 两点在x方向插值,得到点
两点在x方向插值,得到点  的值;最后对
的值;最后对 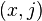 和
和  在 y 方向插值,得到
在 y 方向插值,得到  的值。
的值。
在三维的情况下,需要进行七次插值。可以证明,插值次数随着维数的增长指数增长。
经典Perlin噪声基本满足Perlin提出的噪声条件。但是由于  导数中含有线性分量,在计算相邻点差时会体现出人工效果,不够自然。经典Perlin噪声在进行下文的分形和运算后效果不够自然[2]。
导数中含有线性分量,在计算相邻点差时会体现出人工效果,不够自然。经典Perlin噪声在进行下文的分形和运算后效果不够自然[2]。
这个全是文字说明,下面再来段图解,可以和上面合在一起看。出自 http://webstaff.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf

建议大家看完这个PDF,我最开始看noise的代码,老是觉的不可理喻,至到看到这个图,就理解其中的几个比较主要的步骤。下面看下针对上面的那个例子改写的F# noise版本。


1 type PerlinNoise() = 2 let B = 256 3 let BM,DBN,N = B-1,2*B+2,B*B 4 //let B,BM,N,NM,NP,DBN=256,255,4096,4095,12,(2*256+2) 5 //permutation 排列表 实现一种伪随机的效果 6 let p = Array.create DBN 0 7 //gradient 梯度表 索引在排列表中 8 let pg = Array.create DBN vec3.Zero 9 let curve t = 10 // t * t * (3. - 2. * t) ) 11 t * t * t * (t * (t * 6. - 15.) + 10.) 12 let lerp t a b = a + t*(b-a) 13 //得到点vec在对应维度上(x,y,z)上的二边的索引,以及二边的贡献点,二阶平滑插值 14 let pos vec = 15 //去掉负值 1/B*floor(P)+ONEHALF; 16 let t = vec + float N + 0.5 // Math.Floor(float vec)/(float B) + 1.0/(float (2*B)) 17 //let t = Math.Floor(float vec)/(float B) + 1.0/(float (2*B)) 18 //点d的左边,前面,下面索引 (指的是排列表中的位置索引) 19 let x0 = int (Math.Floor(t)) &&& BM 20 //点d的右边,右面,上面索引 21 let x1 = x0 + 1 &&& BM 22 //点d在当前维度上,用于对应梯度中左边(x轴),前面(z轴),下面(y轴)各点贡献值 23 let u0 = t - Math.Floor(t) 24 //其中u0+(-u1)=1.0,-(1.0-u0) 右边,后边,上面各点贡献值 ( 25 let u1 = u0 - 1.0 26 //二阶平滑位置 27 let cf = curve u0 28 x0,x1,u0,u1,cf 29 let init() = 30 let rand = Random(2) 31 for i = 0 to BM do 32 p.[i] <- i 33 pg.[i] <- vec3(rand.NextDouble()*2.0 - 1.0,rand.NextDouble()*2.0 - 1.0,rand.NextDouble()*2.0 - 1.0) 34 //pg.[i] <- vec2( float (rand.Next()), float (rand.Next())) 35 pg.[B+i] <- pg.[i] 36 for i = 0 to BM do 37 let j = (rand.Next() >>> 5) % BM 38 let t = p.[i] 39 p.[i] <- p.[j] 40 p.[j] <- t 41 p.[i + B] <- p.[i] 42 do 43 init() 44 member this.Noise1 (x:float) = 45 let x0,x1,u0,u1,cx = pos x 46 //得到二点的梯度值. 47 let ug0 = u0 * pg.[p.[x0]].X 48 //-(1.0-f0) 负表示 49 let ug1 = u1 * pg.[p.[x1]].X 50 //u v 平滑位置 noise1位置 51 lerp cx ug0 ug1 52 member this.Noise2 (x,y) = 53 let x0,x1,u0,u1,cx = pos x 54 let y0,y1,v0,v1,cy = pos y 55 //2维中权重也需要混合 下标DBN,p.[x0] + y0 最大为2B 56 let gx0y0 = pg.[p.[p.[x0] + y0]] 57 let gx1y0 = pg.[p.[p.[x1] + y0]] 58 let gx0y1 = pg.[p.[p.[x0] + y1]] 59 let gx1y1 = pg.[p.[p.[x1] + y1]] 60 let mixuv (v3:vec3) u v = v3.X * u + v3.Y * v 61 //yo轴上x混合值 62 let u0v0 = mixuv gx0y0 u0 v0 //gx0y0.X * u0 + gx0y0.Y * v0 63 let u1v0 = mixuv gx1y0 u1 v0//gx1y0.X * u1 + gx1y0.Y * v0 64 let ccx0 = lerp cx u0v0 u1v0 65 //y1轴上x混合值 66 let u0v1 = mixuv gx0y1 u0 v1//gx0y1.X * u0 + gx0y1.Y * v1 67 let u1v1 = mixuv gx1y1 u1 v1//gx1y1.X * u1 + gx1y1.Y * v1 68 let ccx1 = lerp cx u0v1 u1v1 69 //混合二y轴 70 let result = lerp cy ccx0 ccx1 71 // -1 --- 1映射成 0 --- 1 72 result //* 0.5 + 0.5 73 member this.Noise3 (x,y,z) = 74 let x0,x1,u0,u1,cx = pos x 75 let y0,y1,v0,v1,cy = pos y 76 let z0,z1,r0,r1,cz = pos z 77 //权重与当前点(一维左右二个,二维上下左右四个,三维八个)上各分量的点积 78 let mixuvr (v3:vec3) u v r = v3.X * u + v3.Y * v + v3.Z * r 79 //3维中权重也需要混合 zo面 同二维 80 let gx0y0z0 = pg.[p.[p.[x0] + y0] + z0] 81 let gx1y0z0 = pg.[p.[p.[x1] + y0] + z0] 82 let gx0y1z0 = pg.[p.[p.[x0] + y1] + z0] 83 let gx1y1z0 = pg.[p.[p.[x1] + y1] + z0] 84 85 let u0v0r0 = mixuvr gx0y0z0 u0 v0 r0 86 let u1v0r0 = mixuvr gx1y0z0 u1 v0 r0 87 let ccx0z0 = lerp cx u0v0r0 u1v0r0 88 89 let u0v1r0 = mixuvr gx0y1z0 u0 v1 r0 90 let u1v1r0 = mixuvr gx1y1z0 u1 v1 r0 91 let ccx1z0 = lerp cx u0v1r0 u1v1r0 92 93 let ccyz0 = lerp cy ccx0z0 ccx1z0 94 //z1面 同二维 95 let gx0y0r1 = pg.[p.[p.[x0] + y0] + z1] 96 let gx1y0r1 = pg.[p.[p.[x1] + y0] + z1] 97 let gx0y1r1 = pg.[p.[p.[x0] + y1] + z1] 98 let gx1y1r1 = pg.[p.[p.[x1] + y1] + z1] 99 100 let u0v0r1 = mixuvr gx0y0r1 u0 v0 r1 101 let u1v0r1 = mixuvr gx1y0r1 u1 v0 r1 102 let ccx0z1 = lerp cx u0v0r1 u1v0r1 103 104 let u0v1r1 = mixuvr gx0y1r1 u0 v1 r1 105 let u1v1r1 = mixuvr gx1y1r1 u1 v1 r1 106 let ccx1z1 = lerp cx u0v1r1 u1v1r1 107 108 let ccyz1 = lerp cy ccx0z1 ccx1z1 109 //混合z轴 110 lerp cz ccyz0 ccyz1 111 //octave 倍频,amplitude振幅,调整高低,frequency频率,越小间隔越平滑 112 member this.PerlinNoise2(x,y,octave,amplitude,frequency) = 113 let mutable total = 0.0 114 for i in [|0 .. octave - 1|] do 115 let freq = Math.Pow(frequency,float i) 116 let amp = Math.Pow(amplitude,float i) 117 total <- total + this.Noise2(x*freq,y*freq)*amp 118 total 119 //生成一张图片RGBA源,用于测试 120 member this.Test() = 121 init() 122 let arrayrgb = ArrayList<byte>() 123 let mutable maxvalue = 0.0 124 for i in [| 0 .. 255|] do 125 for j in [| 0 .. 255|] do 126 // let r = this.Noise2 (float i + float i/256.,float j + float j/256.) 127 //let r = this.Noise2 (float i,float j ) 128 let r = this.Noise2 (float i/256.,float j/256. ) 129 let color = byte (r*128.) + 128uy 130 arrayrgb.AddRange([| color; color; color;color |]) 131 arrayrgb.ToArray() 132 133 //如果我们想要坐标(i,j,k)的gradient g(i,j,k),而P里预存储了256个gradient, 那么: 134 // g(i, j, k) = P[ ( i + P[ (j + P[k]) mod 256 ] ) mod 256 ]
主要思路前面资料都有说明,这下加些我自己的理解,生成noise时,我们一般需要二个表,一个是排列表-英文permutation,一个是梯度表-英文gradient,如果我们用256个点来组成索引。那么在排列表里会随机放入0-255这256个数值,而梯度表里的数据,默认是放入-1到1的浮点数,当然这都没有定死,256个不需要,我看到有些noise生成里就只有32个,还个-1到1,也有放入0到1而在计算梯度映射成-1到3的代码,这些可以根据你的需求来改动。这里有点要说明,排列表里用256个数字,但是排列表与梯度表的长度应该是2*256(请看代码中的pg.[p.[p.[x0] + y0]] 这种),这里和下面的算法有关,当然,也有直接用256,而在下面计算时映射成正确的索引,如果基本排列表与梯度表如果比用的数据多一倍,那么排列表与梯度表的前半部分和后面部分是一样的。需要指出的是,索引表在这里是随机替换成杂序的,而很多noise生成算法索引表是直接用的Perlin最初给出如int perm[256]= {151,160,137,91,90,15这种256个长度的序列数字,不管是自己生成还是给定的,都是无序的。网上各算法如上面所说,可能各有一些不同,但是都不影响最终生成的效果图。也都满足柏林提出的三个性质。
生成noise的过程,我在代码中都加了注释,主要过程上面的那张图很经典,加些自己的理解,在二维noise中,根据梯度与排列表构成的二维平面中,根据传进来来的二维点x,y,分别找到他在排列表中的位置的上下左右包围它的四个梯度点(对应前面图的i,j),并分别计算与这四个梯度点的位置(对应前面图中的u,v).然后根据四个梯度点对点x,y分别给出的贡献,得到x,y的值。在三维noise,分别对应有六个点,分别是前后左右上下,然后计算是差不多的,大家可以直接分析代码。
关于noise的生成差不多就是如上了,在这里,noise已经生成了能模仿自然界中的平滑变动的信息了,还要Perlin噪声做什么?在上面,可以看到海水的高度不高,那这里,大家肯定直接想到,我把noise生成-1到1的范围映射成-n到n的范围不就好了,下面看下图:

第一张图是noise放大30倍,也就是(-1) - (1)映射成(-30) - (30)的效果,第二个是采用上面的代码,以PerlinNoise2生成的效果,采用以4倍频,每次增加4倍振幅。生成最终高度可能达到1+4+16+64,远远大于30,但是都还是保持平滑的变动。由此可知,noise我们传入的是-1到1,那么他产生的平常效果也是在区间-1到1,映射到n到n+2都是有平滑效果的,而映射成那种-n到n(n大于1)后,平滑变化开始漫漫消失。而映射到-n到n而继续平滑变动,唯有用柏林噪声才行。
关于柏林根据noise叠加的相关说明,大家可以参考如http://freespace.virgin.net/hugo.elias/models/m_perlin.htm,但是不建议最开始看这个,这个讲解是先讲柏林如果构造noise,然后noise如何生成的,容易迷糊。在明白noise的生成过程后,再来看这个倒是非常好的资料。在this.PerlinNoise2(x,y,octave,amplitude,frequency) =中,amplitude,frequency一般来说,相乘等于一,不过也没限制,其中amplitude可以用来控制高度,而frequency控制波形的间隔。
在上面右图是以pNoise.PerlinNoise2(x,z,4,4.0,0.25),生成,下面来看下改动frequency的效果。

上面左图是frequency由0.25变成0.56的效果,而右图是frequency由0.25变成0.11的效果,左图的用来模拟那种山峰倒是不错,在这访海波有种瞎眼了的感觉,而frequency为0.11后,大家可以看到波形之间变化不大。amplitude的是上下振幅,改变这个的效果图就不发了,一想就明白,影响生成的高度的。
其中这个面与高度的代码如下:


1 type Plane(xres,yres,xscale,yscale) = 2 inherit Shape() 3 let xr,yr,xc,yc = xres-1,yres-1,xscale,yscale 4 let vboLen,eboLen = (xres*yres),xr*yr 5 let pNoise = PerlinNoise() 6 override this.Init() = 7 let halfx = (float32 xr) * xscale * 0.5f 8 let halfy = (float32 yr) * yscale * 0.5f 9 let rand = Random(222131) 10 let data = Array2D.init vboLen 6 (fun yx i -> 11 let y = yx / yr 12 let x = yx % xr 13 //012-color-rgb 345-position-xyz 14 if i = 3 then xc * (float32 x) - halfx 15 else if i = 5 then yc * (float32 y) - halfy 16 else 17 let x,z = float (xc * (float32 x) - halfx),float (yc * (float32 y) - halfy) 18 let y1 = float32 (pNoise.Noise2(x,z)) * 30.0f// 19 let y2 = float32 (pNoise.PerlinNoise2(x,z,4,4.0,0.11)) 20 let y3 = float32 (rand.NextDouble()) //* 8.0f 21 let color = float32 (pNoise.Noise2(x,z) + 1.0) * 0.5f 22 if i = 4 then y2 23 else if i = 0 then 0.5f*color 24 else if i = 1 then 0.8f*color 25 else 0.9f*color 26 ) 27 28 let indexs = Array2D.init eboLen 6 (fun yx i -> 29 let y = yx / (yr-1) 30 let x = yx % (xr-1) 31 if i = 0 then (y+0)*xr + x 32 else if i = 1 then (y+1)*xr + x 33 else if i = 2 then (y+0)*xr + x + 1 34 else if i = 3 then (y+0)*xr + x + 1 35 else if i = 4 then (y+1)*xr + x 36 else (y+1)*xr + x + 1 37 ) 38 let mutable vID,eID = 0,0 39 GL.GenBuffers(1,&vID) 40 GL.BindBuffer(BufferTarget.ArrayBuffer,vID) 41 GL.BufferData(BufferTarget.ArrayBuffer,IntPtr (4 * vboLen * 6),data,BufferUsageHint.StaticDraw) 42 43 GL.GenBuffers(1,&eID) 44 GL.BindBuffer(BufferTarget.ElementArrayBuffer,eID) 45 GL.BufferData(BufferTarget.ElementArrayBuffer,IntPtr (4 * eboLen * 6),indexs,BufferUsageHint.StaticDraw) 46 47 this.vboID <- vID 48 this.eboID <- eID 49 this.IsCreate <- true 50 override this.Draw() = 51 if this.IsCreate<>true then this.Init() 52 GL.BindBuffer(BufferTarget.ArrayBuffer,this.vboID) 53 GL.BindBuffer(BufferTarget.ElementArrayBuffer,this.eboID) 54 GL.InterleavedArrays(InterleavedArrayFormat.C3fV3f,0,IntPtr.Zero) 55 GL.DrawElements(BeginMode.Triangles,eboLen * 6,DrawElementsType.UnsignedInt,IntPtr.Zero)
很简单的一段代码,分别是生成点坐标,点颜色,然后是点索引。点坐标与点颜色分别占用3位,排列顺序如012-color-rgb 345-position-xyz,这样主要是为了简洁代码,下面可以直接指定数据的排列顺序InterleavedArrayFormat.C3fV3f。其中y1是noise生成,y2是柏林noise生成,y3是随机点。
上面都是2维的noise应用,对应是2D平面,那么3维noise对应就是3D空间.这里不说3D空间的应用,继续还是针对上面的波浪,可以看到是不动的,如果想要真实如海面的随时间而动,可以应用3维noise,把时间做为参数,传入noise中的一维中来生成噪声值.把上面的代码改下.


1 let x,z = float (xc * (float32 x) - halfx),float (yc * (float32 y) - halfy) 2 let date =float DateTime.Now.Millisecond * 0.1 - 500.0 3 let y1 = float32 (pNoise.Noise3(x,z,date))
需要注意的是,前面2维里因为只生成就不动了,故只需在初始化时调用一次noise生成,而波浪动画不一样,需要每桢来更新数据,就是调用上面的noise生成.在这里,前面有个比较重要的说明一直没说,在这里说下,noise生成的值是伪随机性的,大家看到前面的Rnadom对象,都是给定种子了的,每次他生成的索引表与梯度表都是一样的,同样的参数下,每次noise生成的结果是一样的,当然大家可以替换random种子,会改变生成的noise.所以这里如果大家想着每桢里调用2维noise,生成的结果就是不一样的是错误的,当然你每桢改变种子,用二维来生成,你会发现,每桢的波型变化是杂乱,不自然的.唯有用3维noise,才能得到比较随时间而自然变动的波形.这个效果图在这先不放了,下面会给出着色器版的.
大家这样改后,可能就会发现,卡的完全动不了,因为noise的计算虽然不是很复杂,但是架不住点多,CPU的并行计算能力有限,请看下文,把相关计算放入着色器中,用GPU来计算.然后我们再来看效果.
附件请看下文。


